Percubaan Matematik Tambahan SPM 2021 (Selangor), Kertas 1 (Soalan 1 & 2)

Soalan 1:
$\text{Diberi }g\left(x\right)=\frac{2x-5}{3x-p},x\ne q$

(a)(i) Ungkapkan p dalam sebutan q dan cari g^-1 (x) dalam sebutan p.
(a)(ii)  $\text{Diberi }{g}^{n-1}\left(x\right)=\frac{px-5}{3x-2},x\ne k$ ,
tentukan nilai n dengan membandingkan g^-1 (x) di atas dengan g^n-1 (x) yang diberikan.
Seterusnya, cari nilai k. [5 markah]

(b) Apakah syarat ke atas p supaya g = g^-1 ? [1 markah]


Penyelesaian:
(a)(i)
$\begin{array}{l}3x-p\ne 0\\ 3x\ne p\\ x\ne \frac{p}{3}\\ \mathrm{Diberi}x\ne q\\ \therefore q=\frac{p}{3}\\ p=3q\\ \\ g(x)=\frac{2x-5}{3x-p}\\ \text{Katakan }{g}^{-1}(x)=y\\ g(y)=x\\ \frac{2y-5}{3y-p}=x\\ 2y-5=3xy-px\\ y\left(2-3x\right)=-px+5\\ y\left(3x-2\right)=px-5\\ y=\frac{px-5}{3x-2}\\ \therefore g^{-1}(x)=\frac{px-5}{3x-2}\end{array}$


(a)(ii)
$\begin{array}{l}{g}^{n-1}(x)=g^{-1}(x)=\frac{px-5}{3x-2}\\ \therefore n-1=-1\\ n=0\\ \\ 3x-2\ne 0\\ x\ne \frac{2}{3}\\ k=\frac{2}{3}\end{array}$

(b)
$\begin{array}{l}g(x)=\frac{2x-5}{3x-p}\\ g^{-1}(x)=\frac{px-5}{3x-2}\\ \\ g(x)=g^{-1}(x)\text{ if }p=2\end{array}$

Soalan 2:
Cari julat nilai x bagi 5 < 2x² + x + 4 dan 2x² + x + 4 ≤ 10.
Seterusnya, selesaikan ketaksamaan 5 < 2x²+ x + 4 ≤ 10.
[4 markah]

Penyelesaian:
5 < 2x² + x + 4
0 < 2x² + x – 1
2x² + x – 1 > 0
(2x – 1)(x + 1) > 0
x < -1  atau  x > ½

2x² + x + 4 ≤ 10
2x² + x – 6 ≤ 0
(2x – 3)(x + 2) ≤ 0
-2 ≤ x ≤ 3/2

x < -1, x > ½  atau  -2 ≤ x ≤ 3/2
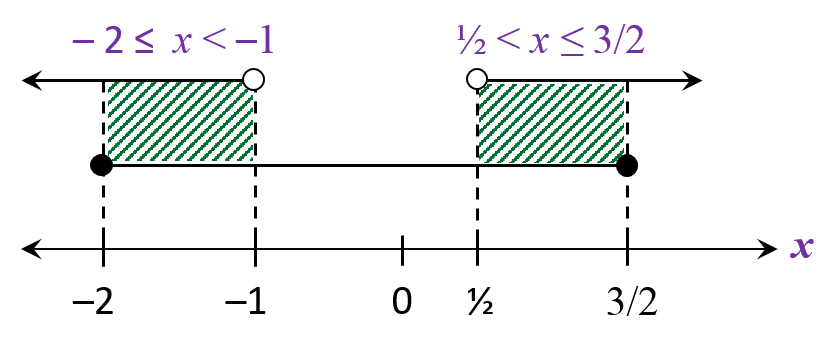-2 ≤ x < -1   atau  ½ < x ≤ 3/2