Soalan 9:
Cari julat nilai k jika persamaan kuadratik 3(x2 – kx – 1) = k – k2 mempunyai dua punca nyata yang berbeza.
Penyelesaian:

Cari julat nilai k jika persamaan kuadratik 3(x2 – kx – 1) = k – k2 mempunyai dua punca nyata yang berbeza.
Penyelesaian:

Soalan 10:
Diberi persamaan kuadratik hx2 – (h + 2)x – (h – 4) = 0 mempunyai punca-punca yang nyata dan berbeza. Cari julat nilai h.
Penyelesaian:

Diberi persamaan kuadratik hx2 – (h + 2)x – (h – 4) = 0 mempunyai punca-punca yang nyata dan berbeza. Cari julat nilai h.
Penyelesaian:

Soalan 11:
Rajah di bawah menunjukkan graf fungsi kuadratik f(x) = (x + 3)2 + 2h – 6, dengan keadaan h ialah pemalar.
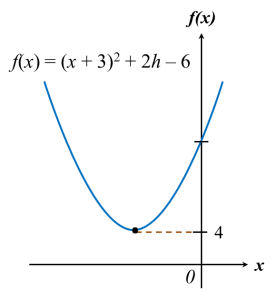
(a) Nyatakan persamaan paksi simetri bagi lengkung itu.
(b) Diberi nilai minimum bagi fungsi itu ialah 4, cari nilai h.
Penyelesaian:
(a)
Apabila x + 3 = 0
x = –3
Maka, persamaan paksi simetri bagi lengkung itu ialah x = –3.
(b)
Apabila x + 3 = 0, f(x) = 2h – 6
Nilai minimum bagi f(x) ialah 2h – 6.
Maka, 2h – 6 = 4
2h = 10
h = 5
Rajah di bawah menunjukkan graf fungsi kuadratik f(x) = (x + 3)2 + 2h – 6, dengan keadaan h ialah pemalar.

(a) Nyatakan persamaan paksi simetri bagi lengkung itu.
(b) Diberi nilai minimum bagi fungsi itu ialah 4, cari nilai h.
Penyelesaian:
(a)
Apabila x + 3 = 0
x = –3
Maka, persamaan paksi simetri bagi lengkung itu ialah x = –3.
(b)
Apabila x + 3 = 0, f(x) = 2h – 6
Nilai minimum bagi f(x) ialah 2h – 6.
Maka, 2h – 6 = 4
2h = 10
h = 5
macam mana mau selesaikan soalan
x²+6(p+3)x+9p(p+5)=0
-soalan minta cari julat nilai p .