Soalan 11:
(a) Didapati bahawa kebarangkalian satu produk dari sebuah syarikat dapat dijual ialah 19/20.
Jika dalam satu bulan tertentu, syarikat tersebut menghasilkan 820 unit produk, cari min dan sisihan piawai bilangan produk yang dijangka akan dijual pada bulan itu. [3 markah]
(b) Terdapat 25 orang murid di dalam sebuah kelas. Seorang guru ingin memilih beberapa orang murid dari kelas itu untuk menyertai satu permainan.
(i) Diberi bahawa bilangan cara berbeza memilih r orang murid adalah sama dengan bilangan cara berbeza memilih (r + 13) orang murid. Cari nilai r.
(ii) Guru itu memutuskan untuk memilih 8 orang murid untuk menyertai permainan itu. Dia mahu memilih bilangan yang sama bagi murid lelaki dan murid perempuan.
Jika murid-murid ini hendak disusun dalam satu baris, cari bilangan cara berbeza supaya murid lelaki tidak berada bersebelahan.
[4 markah]
Penyelesaian:
(a)
$$ \begin{aligned} n & =820 \\ p & =\frac{19}{20} \\ q & =1-\frac{19}{20} \\ & =\frac{1}{20} \end{aligned} $$
$$ \text { Min, } \begin{aligned} \mu & =n p \\ & =(820)\left(\frac{19}{20}\right) \\ & =779 \end{aligned} $$
$$ \begin{aligned} &\text { Sisihan piawai, } \sigma=\sqrt{n p q}\\ &\begin{aligned} & =\sqrt{(820)\left(\frac{19}{20}\right)\left(\frac{1}{20}\right)} \\ & =\sqrt{\left(\frac{779}{20}\right)} \\ & =6.241 \end{aligned} \end{aligned} $$
(b)(i)
$$ \begin{aligned} &\text { Formula }{ }^n C_r={ }^n C_{n-r}\\ &r+(n-r)=n \end{aligned} $$
$$ \begin{aligned} n & =25 \\ { }^{25} C_r & ={ }^{25} C_{r+13} \\ r+(r+13) & =25 \\ 2 r+13 & =25 \\ 2 r & =12 \\ r & =6 \end{aligned} $$
(b)(ii)
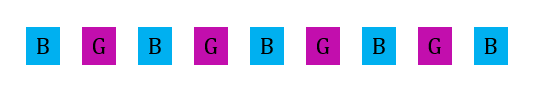
4 murid perempuan dipilih = 4!
murid lelaki dipilih supaya mereka tidak berada bersebelahan = 5P4
Maka, bilangan cara = 4! × 5P4
= 2880
(a) Didapati bahawa kebarangkalian satu produk dari sebuah syarikat dapat dijual ialah 19/20.
Jika dalam satu bulan tertentu, syarikat tersebut menghasilkan 820 unit produk, cari min dan sisihan piawai bilangan produk yang dijangka akan dijual pada bulan itu. [3 markah]
(b) Terdapat 25 orang murid di dalam sebuah kelas. Seorang guru ingin memilih beberapa orang murid dari kelas itu untuk menyertai satu permainan.
(i) Diberi bahawa bilangan cara berbeza memilih r orang murid adalah sama dengan bilangan cara berbeza memilih (r + 13) orang murid. Cari nilai r.
(ii) Guru itu memutuskan untuk memilih 8 orang murid untuk menyertai permainan itu. Dia mahu memilih bilangan yang sama bagi murid lelaki dan murid perempuan.
Jika murid-murid ini hendak disusun dalam satu baris, cari bilangan cara berbeza supaya murid lelaki tidak berada bersebelahan.
[4 markah]
Penyelesaian:
(a)
$$ \begin{aligned} n & =820 \\ p & =\frac{19}{20} \\ q & =1-\frac{19}{20} \\ & =\frac{1}{20} \end{aligned} $$
$$ \text { Min, } \begin{aligned} \mu & =n p \\ & =(820)\left(\frac{19}{20}\right) \\ & =779 \end{aligned} $$
$$ \begin{aligned} &\text { Sisihan piawai, } \sigma=\sqrt{n p q}\\ &\begin{aligned} & =\sqrt{(820)\left(\frac{19}{20}\right)\left(\frac{1}{20}\right)} \\ & =\sqrt{\left(\frac{779}{20}\right)} \\ & =6.241 \end{aligned} \end{aligned} $$
(b)(i)
$$ \begin{aligned} &\text { Formula }{ }^n C_r={ }^n C_{n-r}\\ &r+(n-r)=n \end{aligned} $$
$$ \begin{aligned} n & =25 \\ { }^{25} C_r & ={ }^{25} C_{r+13} \\ r+(r+13) & =25 \\ 2 r+13 & =25 \\ 2 r & =12 \\ r & =6 \end{aligned} $$
(b)(ii)
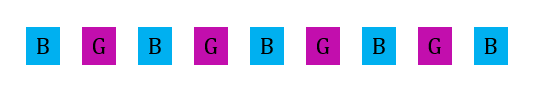
4 murid perempuan dipilih = 4!
murid lelaki dipilih supaya mereka tidak berada bersebelahan = 5P4
Maka, bilangan cara = 4! × 5P4
= 2880