3.5 Pengamiran Sebagai Penghasiltambahan Luas

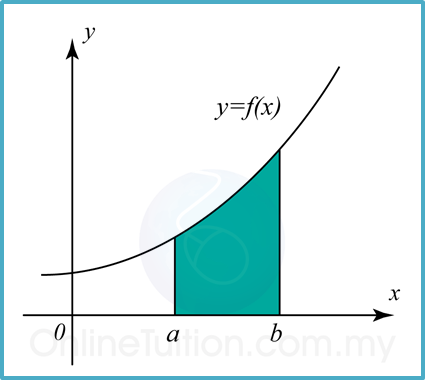
3.5 Pengamiran Sebagai Penghasiltambahan Luas

(A) Luas di bawah suatu lengkung dengan paksi-x

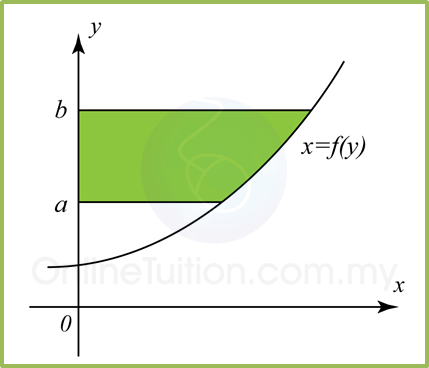
\begin{array}{l} Luas rantau berlorek, \\ L = \int_{a}^{b} y d x \end{array}

(B) Luas di bawah suatu lengkung dengan paksi-y

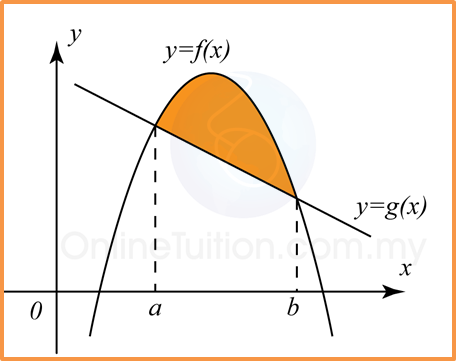
\begin{array}{l} Luas rantau berlorek, \\ L = \int_{a}^{b} x d y \end{array}

(C) Luas di bawah suatu lengkung dengan suatu garis lurus

\begin{array}{l} Luas rantau berlorek, \\ L = \int_{a}^{b} f (x) d x - \int_{a}^{b} g (x) d x \end{array}

Contoh 1:

Cari luas rantau berlorek.

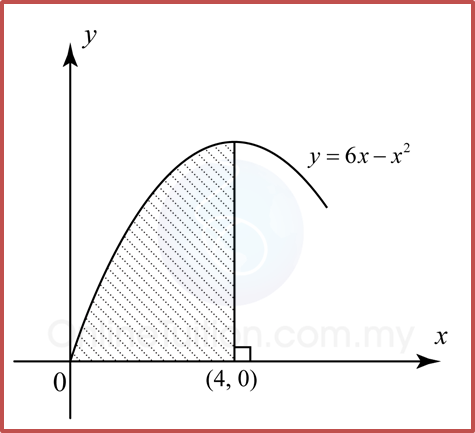
Penyelesaian:

Luas rantau berlorek, L

\begin{array}{l} = \int_{a}^{b} y d x \\ = \int_{0}^{4} (6 x - x^{2}) d x \\ = {[\frac{6 x^{2}}{2} - \frac{x^{3}}{3}]}_{0}^{4} \\ = [3 {(4)}^{2} - \frac{{(4)}^{3}}{3}] - 0 \\ = 26 \frac{2}{3} {unit}^{2} \end{array}

Contoh 2:

Cari luas rantau berlorek.

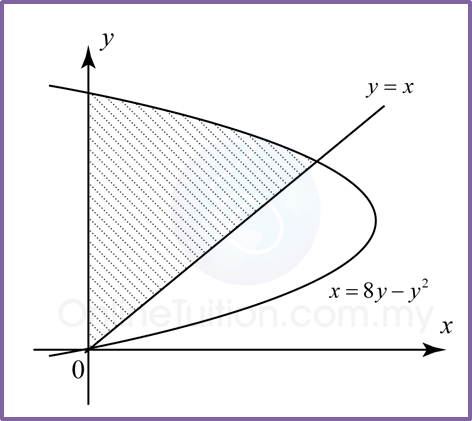
Penyelesaian:

y = x —–(1)

x = 8y – y² —–(2)

Gantikan (1) ke dalam (2),

y = 8y – y²

y²– 7y = 0

y (y – 7) = 0

y = 0 atau 7

Dari (1), x = 0 atau 7

Maka, titik persilangan antara lengkung dengan garis lurus ialah (0, 0) dan (7, 7).

Titik persilangan lengkung dengan paksi-y adalah,

x = 8y – y²

pada y-axis, x = 0

0 = 8y – y²

y (y – 8) = 0

y = 0 atau 8

Luas kawasan berlorek = (A₁) Luas segitiga + (A₂) Luas di bawah lengkung dari y = 7 hingga y = 8.

\begin{array}{l} = \frac{1}{2} \times tapak \times tinggi + \int_{7}^{8} x d y \\ = \frac{1}{2} \times (7) (7) + \int_{7}^{8} (8 y - y^{2}) d y \\ = \frac{49}{2} + {[\frac{8 y^{2}}{2} - \frac{y^{3}}{3}]}_{7}^{8} \\ = 24 \frac{1}{2} + [4 {(8)}^{2} - \frac{{(8)}^{3}}{3}] - [4 {(7)}^{2} - \frac{{(7)}^{3}}{3}] \\ = 24 \frac{1}{2} + 85 \frac{1}{3} - 81 \frac{2}{3} \\ = 28 \frac{1}{6} {unit}^{2} \end{array}