3.6 Pengamiran Sebagai Penghasiltambahan Isi padu

3.6 Pengamiran Sebagai Penghasiltambahan Isi padu

(1).

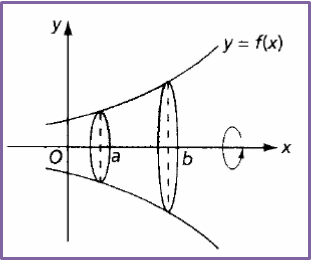
Isi padu yang dijanakan apabila rantau berlorek dikisarkan melalui 360° pada paksi-x

I_{x} = π \int_{a}^{b} y^{2} d x

(2).

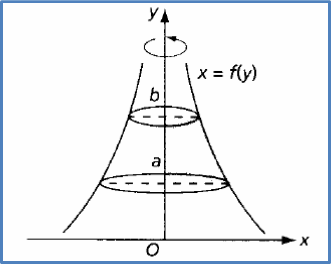
Isi padu yang dijanakan apabila rantau berlorek dikisarkan melalui 360° pada paksi-y

I_{y} = π \int_{a}^{b} x^{2} d y

Contoh 1:

Hitung isi padu pepejal yang dijanakan apabila rantau berlorek di bawah dikisarkan melalui 360° pada paksi-x.

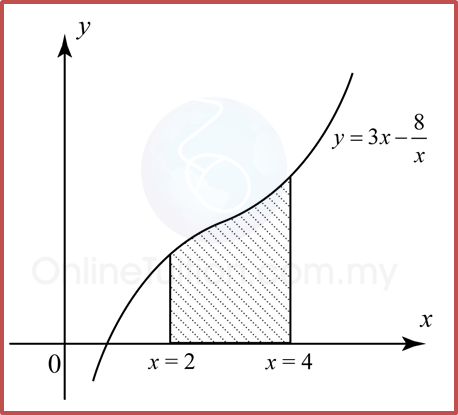
Penyelesaian:

Isi padu yang dijanakan, I_x

\begin{array}{l} I_{x} = π \int_{a}^{b} y^{2} d x \\ I_{x} = π \int_{2}^{4} {(3 x - \frac{8}{x})}^{2} d x \\ I_{x} = π \int_{2}^{4} (3 x - \frac{8}{x}) (3 x - \frac{8}{x}) d x \\ I_{x} = π \int_{2}^{4} (9 x^{2} - 48 + \frac{64}{x^{2}}) d x \\ I_{x} = π {[\frac{9 x^{3}}{3} - 48 x + \frac{64 x^{- 1}}{- 1}]}_{2}^{4} \\ I_{x} = π {[3 x^{3} - 48 x - \frac{64}{x}]}_{2}^{4} \\ I_{x} = π [(3 {(4)}^{3} - 48 (4) - \frac{64}{4}) - (3 {(2)}^{3} - 48 (2) - \frac{64}{2})] \\ I_{x} = π (- 16 + 104) \\ I_{x} = 88 π u n i t^{3} \end{array}

Contoh 2:

Hitung isi padu pepejal yang dijanakan apabila rantau berlorek di bawah dikisarkan melalui 360° pada paksi-y.

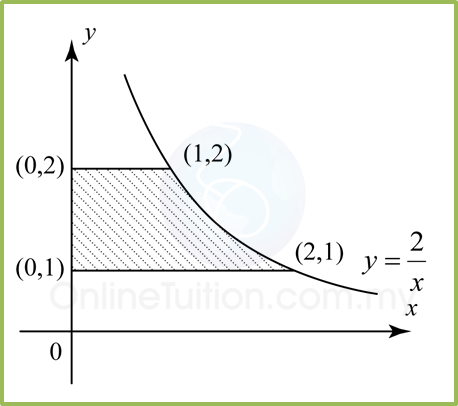
Penyelesaian:

Isi padu yang dijanakan, I_y

\begin{array}{l} I_{y} = π \int_{a}^{b} x^{2} d y \\ I_{y} = π \int_{1}^{2} {(\frac{2}{y})}^{2} d y \\ I_{y} = π \int_{1}^{2} (\frac{4}{y^{2}}) d y \\ I_{y} = π \int_{1}^{2} 4 y^{- 2} d y \\ I_{y} = π {[\frac{4 y^{- 1}}{- 1}]}_{1}^{2} = π {[- \frac{4}{y}]}_{1}^{2} \\ I_{y} = π [(- \frac{4}{2}) - (- \frac{4}{1})] \\ I_{y} = 2 π u n i t^{3} \end{array}