Soalan 11:
Rajah di bawah menunjukkan graf fungsi kuadratik f(x) = (x + 3)2 + 2h – 6, dengan keadaan h ialah pemalar.
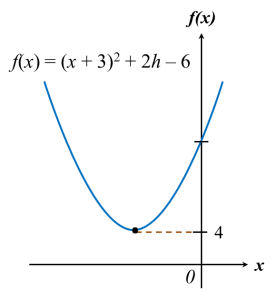
(a) Nyatakan persamaan paksi simetri bagi lengkung itu.
(b) Diberi nilai minimum bagi fungsi itu ialah 4, cari nilai h.
Penyelesaian:
(a)
Apabila x + 3 = 0
x = –3
Maka, persamaan paksi simetri bagi lengkung itu ialah x = –3.
(b)
Apabila x + 3 = 0, f(x) = 2h – 6
Nilai minimum bagi f(x) ialah 2h – 6.
Maka, 2h – 6 = 4
2h = 10
h = 5
Rajah di bawah menunjukkan graf fungsi kuadratik f(x) = (x + 3)2 + 2h – 6, dengan keadaan h ialah pemalar.

(a) Nyatakan persamaan paksi simetri bagi lengkung itu.
(b) Diberi nilai minimum bagi fungsi itu ialah 4, cari nilai h.
Penyelesaian:
(a)
Apabila x + 3 = 0
x = –3
Maka, persamaan paksi simetri bagi lengkung itu ialah x = –3.
(b)
Apabila x + 3 = 0, f(x) = 2h – 6
Nilai minimum bagi f(x) ialah 2h – 6.
Maka, 2h – 6 = 4
2h = 10
h = 5
Soalan 12 (SPM 2017 – 4 markah):
Fungsi kuadratik f ditakrifkan oleh f(x) = x2 + 4x + h, dengan keadaan h ialah pemalar.
(a) Ungkapkan f(x) dalam bentuk (x + m)2 + n, dengan keadaan m dan n ialah pemalar.
(b) Diberi nilai minimum bagi f(x) ialah 8, cari nilai h.
Penyelesaian:
(a)
f(x) = x2 + 4x + h
= x2 + 4x + (2)2 – (2)2 + h
= (x + 2)2 – 4 + h
(b)
Diberi nilai minimum bagi f(x) = 8
– 4 + h = 8
h = 12
Fungsi kuadratik f ditakrifkan oleh f(x) = x2 + 4x + h, dengan keadaan h ialah pemalar.
(a) Ungkapkan f(x) dalam bentuk (x + m)2 + n, dengan keadaan m dan n ialah pemalar.
(b) Diberi nilai minimum bagi f(x) ialah 8, cari nilai h.
Penyelesaian:
(a)
f(x) = x2 + 4x + h
= x2 + 4x + (2)2 – (2)2 + h
= (x + 2)2 – 4 + h
(b)
Diberi nilai minimum bagi f(x) = 8
– 4 + h = 8
h = 12
Soalan 13 (SPM 2017 – 3 markah):
Cari julat nilai x dengan keadaan fungsi kuadratik f(x) = 6 + 5x – x2 ialah negatif.
Penyelesaian:
(a)
f(x) < 0
6 + 5x – x2 < 0
(6 – x)(x + 1) < 0
x < –1, x > 6
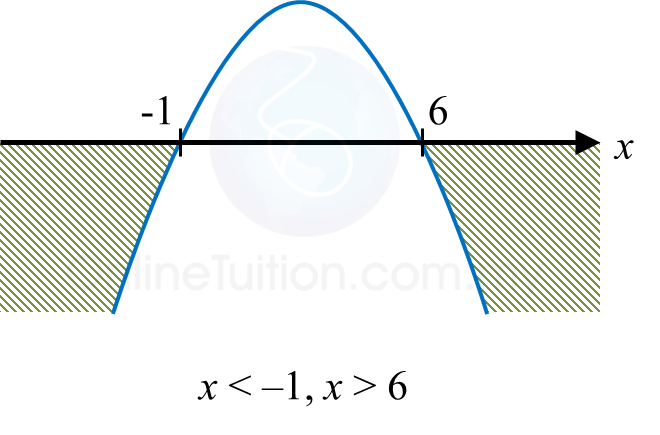
Cari julat nilai x dengan keadaan fungsi kuadratik f(x) = 6 + 5x – x2 ialah negatif.
Penyelesaian:
(a)
f(x) < 0
6 + 5x – x2 < 0
(6 – x)(x + 1) < 0
x < –1, x > 6

Soalan 14 (SPM 2017 – 4 markah):
(a) Diberi bahawa satu dari punca-punca bagi persamaan kuadratik x2 + (p +3)x – p2 = 0, dengan keadaan p ialah pemalar, adalah negatif kepada yang satu lagi.
Cari nilai bagi hasil darab punca.
(b) Diberi bahawa persamaan kuadratik mx2 – 5nx + 4m = 0, dengan keadaan m dan n ialah pemalar, mempunyai dua punca yang sama.
Cari m : n.
Penyelesaian:
(a)
(b)
(a) Diberi bahawa satu dari punca-punca bagi persamaan kuadratik x2 + (p +3)x – p2 = 0, dengan keadaan p ialah pemalar, adalah negatif kepada yang satu lagi.
Cari nilai bagi hasil darab punca.
(b) Diberi bahawa persamaan kuadratik mx2 – 5nx + 4m = 0, dengan keadaan m dan n ialah pemalar, mempunyai dua punca yang sama.
Cari m : n.
Penyelesaian:
(a)
(b)
Soalan 15 (SPM 2018 – 3 markah):
Rajah 8 menunjukkan graf y = a (x – p)2 + q, dengan keadaan a, p dan q ialah pemalar. Garis lurus y = –8 ialah tangen kepada lengkung pada titik H.
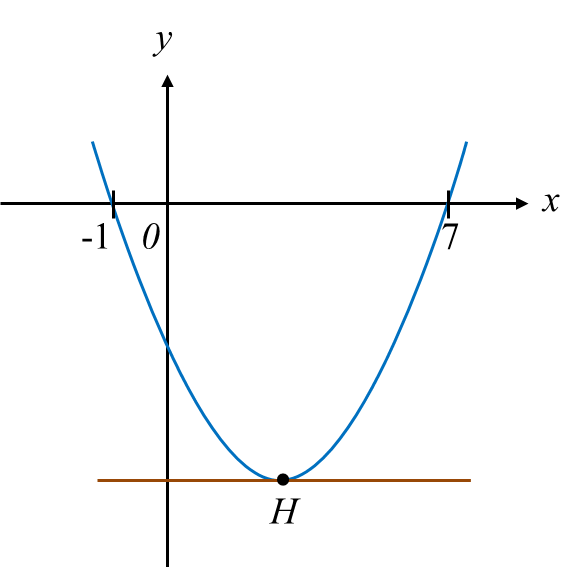 Rajah 8
Rajah 8
(a) Nyatakan koordinat H.
(b) Cari nilai a.
Penyelesaian:
(a)
(b)
Rajah 8 menunjukkan graf y = a (x – p)2 + q, dengan keadaan a, p dan q ialah pemalar. Garis lurus y = –8 ialah tangen kepada lengkung pada titik H.
 Rajah 8
Rajah 8(a) Nyatakan koordinat H.
(b) Cari nilai a.
Penyelesaian:
(a)
(b)
Soalan 16 (SPM 2018 – 3 markah):
Faizal mempunyai sekeping papan lapis berbentuk segi empat tepat yang berukuran 3x meter panjang dan 2x meter lebar. dia memotong sebahagian daripada papan lapis itu kepada bentuk segi empat sama yang bersisi x meter untuk membuat permukaan meja.
Cari julat nilai x jika luas papan lapis yang tinggal adalah sekurang-kurangnya (x2 + 4) meter2.
Penyelesaian:
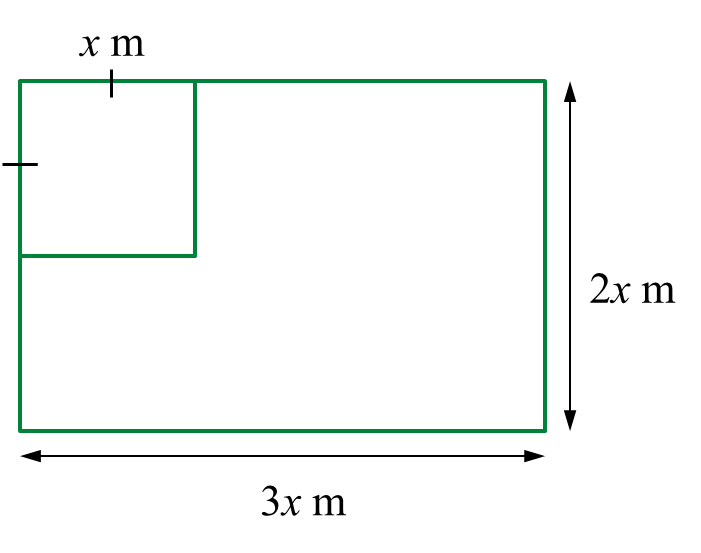
Luas papan berlapis – luas segi empat sama ≥ (x2 + 4)
3x(2x) – x2 ≥ x2 + 4
6x2 – x2 – x2 ≥ 4
4x2 ≥ 4
x2 – 1 ≥ 0
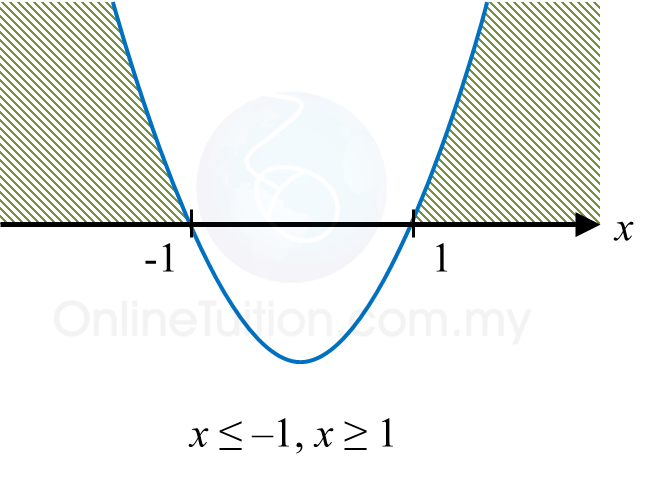
(x + 1)(x – 1) ≥ 0
x ≤ –1 or x ≥ 1
Maka, x ≥ 1 (panjang > 0)
Faizal mempunyai sekeping papan lapis berbentuk segi empat tepat yang berukuran 3x meter panjang dan 2x meter lebar. dia memotong sebahagian daripada papan lapis itu kepada bentuk segi empat sama yang bersisi x meter untuk membuat permukaan meja.
Cari julat nilai x jika luas papan lapis yang tinggal adalah sekurang-kurangnya (x2 + 4) meter2.
Penyelesaian:

Luas papan berlapis – luas segi empat sama ≥ (x2 + 4)
3x(2x) – x2 ≥ x2 + 4
6x2 – x2 – x2 ≥ 4
4x2 ≥ 4
x2 – 1 ≥ 0
(x + 1)(x – 1) ≥ 0
x ≤ –1 or x ≥ 1
Maka, x ≥ 1 (panjang > 0)

Soalan 17 (SPM 2015 – 3 markah):
Graf fungsi kuadratik f(x) =px2 – 8x + q, dengan keadaan p dan q ialah pemalar, mempunyai satu titik maksimum.
(a) Diberi p ialah suatu integer dengan keadaan -2 < p <2, nyatakan nilai p.
(b) Menggunakan jawapan dari 3(a), cari nilai q apabila graf itu menyentuh paksi-x pada satu titik.
[3 markah]
Penyelesaian:
(a) p = -1
(b)
$$ \begin{aligned} & f(x)=-x^2-8 x+q \\ & a=-1, b=-8, c=q \\ & b^2-4 a c=0 \\ & (-8)^2-4(-1) q=0 \\ & 64+4 q=0 \\ & 4 q=-64 \\ & q=-16 \end{aligned} $$
Graf fungsi kuadratik f(x) =px2 – 8x + q, dengan keadaan p dan q ialah pemalar, mempunyai satu titik maksimum.
(a) Diberi p ialah suatu integer dengan keadaan -2 < p <2, nyatakan nilai p.
(b) Menggunakan jawapan dari 3(a), cari nilai q apabila graf itu menyentuh paksi-x pada satu titik.
[3 markah]
Penyelesaian:
(a) p = -1
(b)
$$ \begin{aligned} & f(x)=-x^2-8 x+q \\ & a=-1, b=-8, c=q \\ & b^2-4 a c=0 \\ & (-8)^2-4(-1) q=0 \\ & 64+4 q=0 \\ & 4 q=-64 \\ & q=-16 \end{aligned} $$
Soalan 18 (SPM 2015 – 2 markah):
Diberi -7 ialah satu daripada punca persamaan kuadratik (x + k)2 = 16, dengan keadaan k ialah pemalar. Cari nilai-nilai k.
[2 markah]
Penyelesaian:
$$ \begin{aligned} (x+k)^2= & 16 \\ \sqrt{(-7+k)^2} & = \pm \sqrt{16} \\ -7+k & = \pm 4 \\ -7+k & =4 \\ k & =4+7=11 \\ -7+k & =-4 \\ k & =-4+7=3 \end{aligned} $$
Diberi -7 ialah satu daripada punca persamaan kuadratik (x + k)2 = 16, dengan keadaan k ialah pemalar. Cari nilai-nilai k.
[2 markah]
Penyelesaian:
$$ \begin{aligned} (x+k)^2= & 16 \\ \sqrt{(-7+k)^2} & = \pm \sqrt{16} \\ -7+k & = \pm 4 \\ -7+k & =4 \\ k & =4+7=11 \\ -7+k & =-4 \\ k & =-4+7=3 \end{aligned} $$
Soalan 19 (SPM 2019):
Rajah 1 menunjukkan graf bagi fungsi kuadratik
$$ f(x)=\frac{p}{x^n}+q x+r $$
dengan keadaan p, q, r, n dan u ialah pemalar.
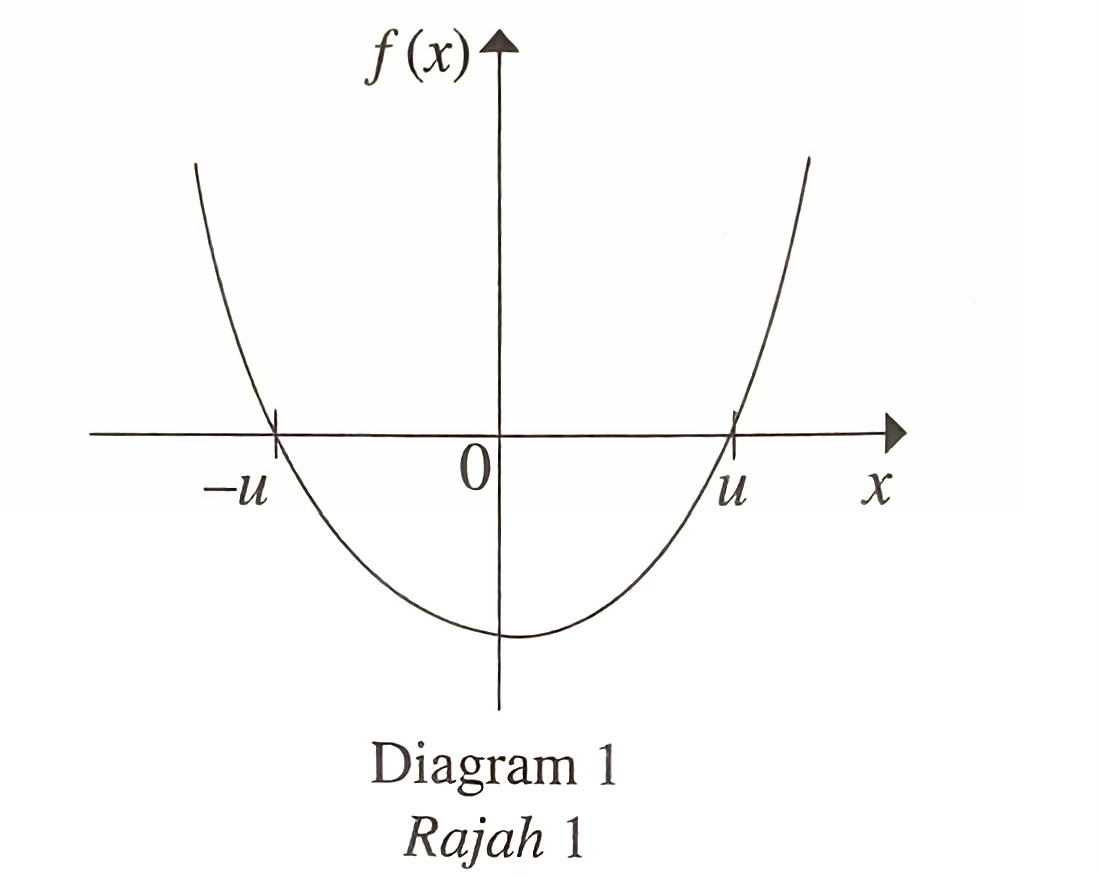 (a) Nyatakan nilai n.
(a) Nyatakan nilai n.
(b) Jika f(x) = 0 dan hasil darab punca ialah r, nyatakan nilai
(i) q,
(ii) p.
[3 markah]
Penyelesaian:
(a)
$$ \begin{aligned} & x^{-n}=x^2 \\ & -n=2 \\ & n=-2 \end{aligned} $$
(b)
$$ \begin{aligned} & f(x)=p x^2+q x+r \\ & p x^2+q x+r=0 \\ & a=p, b=q, c=r \end{aligned} $$
$$ \begin{aligned} &\text { Hasil darab punca }=r\\ &\begin{aligned} & \frac{c}{a}=r \\ & \frac{r}{p}=r \\ & r=p r \end{aligned} \end{aligned} $$
$$ \begin{aligned} & \text { Hasil tambah punca }=-\frac{b}{a} \\ & u+(-u)=-\frac{q}{p} \\ & -\frac{q}{1}=0 \\ & q=0 \end{aligned} $$
$$ \begin{aligned} & r-p r=0 \\ & r(1-p)=0 \\ & r=0, p=1 \end{aligned} $$ (i) q = 0 (ii) p = 1
Rajah 1 menunjukkan graf bagi fungsi kuadratik
$$ f(x)=\frac{p}{x^n}+q x+r $$
dengan keadaan p, q, r, n dan u ialah pemalar.
 (a) Nyatakan nilai n.
(a) Nyatakan nilai n.(b) Jika f(x) = 0 dan hasil darab punca ialah r, nyatakan nilai
(i) q,
(ii) p.
[3 markah]
Penyelesaian:
(a)
$$ \begin{aligned} & x^{-n}=x^2 \\ & -n=2 \\ & n=-2 \end{aligned} $$
(b)
$$ \begin{aligned} & f(x)=p x^2+q x+r \\ & p x^2+q x+r=0 \\ & a=p, b=q, c=r \end{aligned} $$
$$ \begin{aligned} &\text { Hasil darab punca }=r\\ &\begin{aligned} & \frac{c}{a}=r \\ & \frac{r}{p}=r \\ & r=p r \end{aligned} \end{aligned} $$
$$ \begin{aligned} & \text { Hasil tambah punca }=-\frac{b}{a} \\ & u+(-u)=-\frac{q}{p} \\ & -\frac{q}{1}=0 \\ & q=0 \end{aligned} $$
$$ \begin{aligned} & r-p r=0 \\ & r(1-p)=0 \\ & r=0, p=1 \end{aligned} $$ (i) q = 0 (ii) p = 1
Soalan 20 (SPM 2019):
Graf bagi fungsi kuadratik f(x) = 3[2h – (x – 1)2], dengan keadaan h ialah pemalar, mempunyai titik maksimum (1, h – 10).
(a) Nyatakan nilai h.
(b) Nyatakan jenis punca bagi f(x) = 0. Justifikasikan jawapan anda.
[3 markah]
Penyelesaian:
(a)
$$ \begin{aligned} &f(x)=6 h-3(x-1)^2\\ &\text { Nilai maksimum }=6 h \end{aligned} $$
$$ \begin{aligned} & h-10=6 h \\ & -10=5 h \\ & h=-2 \end{aligned} $$
(b)
$$ \begin{aligned} & f(x)=0 \\ & 6(-2)-3(x-1)^2=0 \\ & -12-3\left(x^2-2 x+1\right)=0 \\ & -12-3 x^2+6 x-3=0 \\ & 3 x^2-6 x+15=0 \\ & x^2-2 x+5=0 \\ & a=1, b=-2, c=5 \\ & \text { Nilai } b^2-4 a c \\ & =(-2)^2-4(1)(5) \\ & =4-20 \\ & =-16 \\ & b^2-4 a c<0, \text { Tiada punca } \end{aligned} $$
Graf bagi fungsi kuadratik f(x) = 3[2h – (x – 1)2], dengan keadaan h ialah pemalar, mempunyai titik maksimum (1, h – 10).
(a) Nyatakan nilai h.
(b) Nyatakan jenis punca bagi f(x) = 0. Justifikasikan jawapan anda.
[3 markah]
Penyelesaian:
(a)
$$ \begin{aligned} &f(x)=6 h-3(x-1)^2\\ &\text { Nilai maksimum }=6 h \end{aligned} $$
$$ \begin{aligned} & h-10=6 h \\ & -10=5 h \\ & h=-2 \end{aligned} $$
(b)
$$ \begin{aligned} & f(x)=0 \\ & 6(-2)-3(x-1)^2=0 \\ & -12-3\left(x^2-2 x+1\right)=0 \\ & -12-3 x^2+6 x-3=0 \\ & 3 x^2-6 x+15=0 \\ & x^2-2 x+5=0 \\ & a=1, b=-2, c=5 \\ & \text { Nilai } b^2-4 a c \\ & =(-2)^2-4(1)(5) \\ & =4-20 \\ & =-16 \\ & b^2-4 a c<0, \text { Tiada punca } \end{aligned} $$