Soalan 21 (SPM 2017 – 3 markah):
Rajah 5 menunjukkan graf bagi fungsi f : x → |1 – 2x| untuk domain –2 ≤ x ≤ 4.
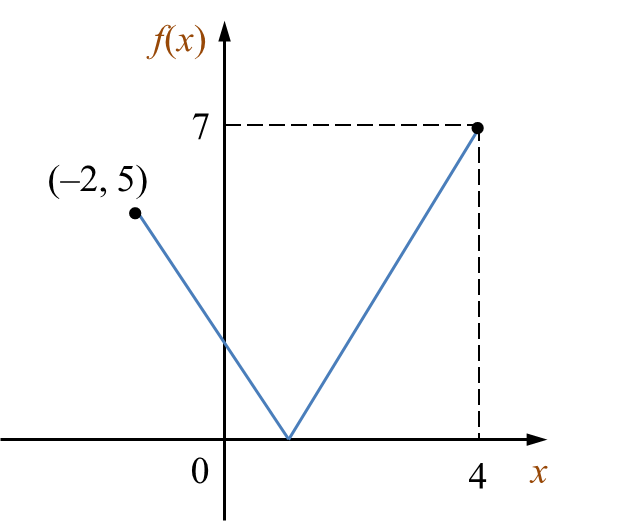 Rajah 5
Rajah 5
Nyatakan
(a) objek bagi 7,
(b) imej bagi 3,
(c) domain bagi 0 ≤ f(x) ≤ 5.
Penyelesaian:
(a)
Objek bagi 7 ialah 4.
(b)
f (x) = |1 – 2x|
f (3) = |1 – 2(3)|
= |1 – 6|
= |–5|
= 5
Imej bagi 3 ialah 5.
(c)
|1 – 2x| = 5
1 – 2x = ±5
Diberi apabila f(x) = 5, x = –2.
Apabila f(x) = –5
1 – 2x = –5
2x = 6
x = 3
Domain: –2 ≤ x ≤ 3.
Rajah 5 menunjukkan graf bagi fungsi f : x → |1 – 2x| untuk domain –2 ≤ x ≤ 4.
 Rajah 5
Rajah 5 Nyatakan
(a) objek bagi 7,
(b) imej bagi 3,
(c) domain bagi 0 ≤ f(x) ≤ 5.
Penyelesaian:
(a)
Objek bagi 7 ialah 4.
(b)
f (x) = |1 – 2x|
f (3) = |1 – 2(3)|
= |1 – 6|
= |–5|
= 5
Imej bagi 3 ialah 5.
(c)
|1 – 2x| = 5
1 – 2x = ±5
Diberi apabila f(x) = 5, x = –2.
Apabila f(x) = –5
1 – 2x = –5
2x = 6
x = 3
Domain: –2 ≤ x ≤ 3.
Soalan 22 (SPM 2017 – 4 markah):
Diberi fungsi g : x → 2x – 8, cari
Penyelesaian:
(a)
(b)
Diberi fungsi g : x → 2x – 8, cari
Penyelesaian:
(a)
(b)
Soalan 23 (SPM 2015):
Diberi fungsi f(x) = 3x dan g(x) = h – kx, dengan keadaan h dan k ialah pemalar. Ungkapkan h dalam sebutan k dengan keadaan gf(1) = 4.
[3 markah]
Penyelesaian:
$$ \begin{aligned} & g f(x)=g(3 x) \\ & =h-k(3 x) \\ & =h-3 k x \\ & g f(1)=h-3 k(1)=4 \\ & h-3 k=4 \\ & h=4+3 k \end{aligned} $$
Diberi fungsi f(x) = 3x dan g(x) = h – kx, dengan keadaan h dan k ialah pemalar. Ungkapkan h dalam sebutan k dengan keadaan gf(1) = 4.
[3 markah]
Penyelesaian:
$$ \begin{aligned} & g f(x)=g(3 x) \\ & =h-k(3 x) \\ & =h-3 k x \\ & g f(1)=h-3 k(1)=4 \\ & h-3 k=4 \\ & h=4+3 k \end{aligned} $$
Soalan 24 (SPM 2015):
Rajah 1 menunjukkan fungsi gubahan gf yang memetakan x kepada z.
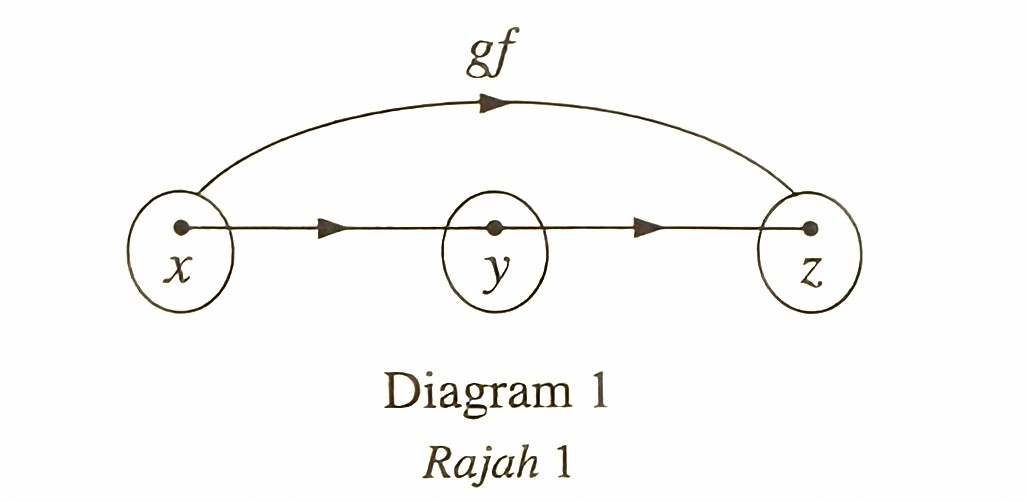
Nyatakan
(a) fungsi yang memetakan x kepada y,
(b) g-1(z).
[2 markah]
Penyelesaian:
(a) fungsi f
(b) g-1(z) = y
Rajah 1 menunjukkan fungsi gubahan gf yang memetakan x kepada z.

Nyatakan
(a) fungsi yang memetakan x kepada y,
(b) g-1(z).
[2 markah]
Penyelesaian:
(a) fungsi f
(b) g-1(z) = y
Soalan 25 (SPM 2019):
Rajah 2 menunjukkan hubungan bagi tiga set.
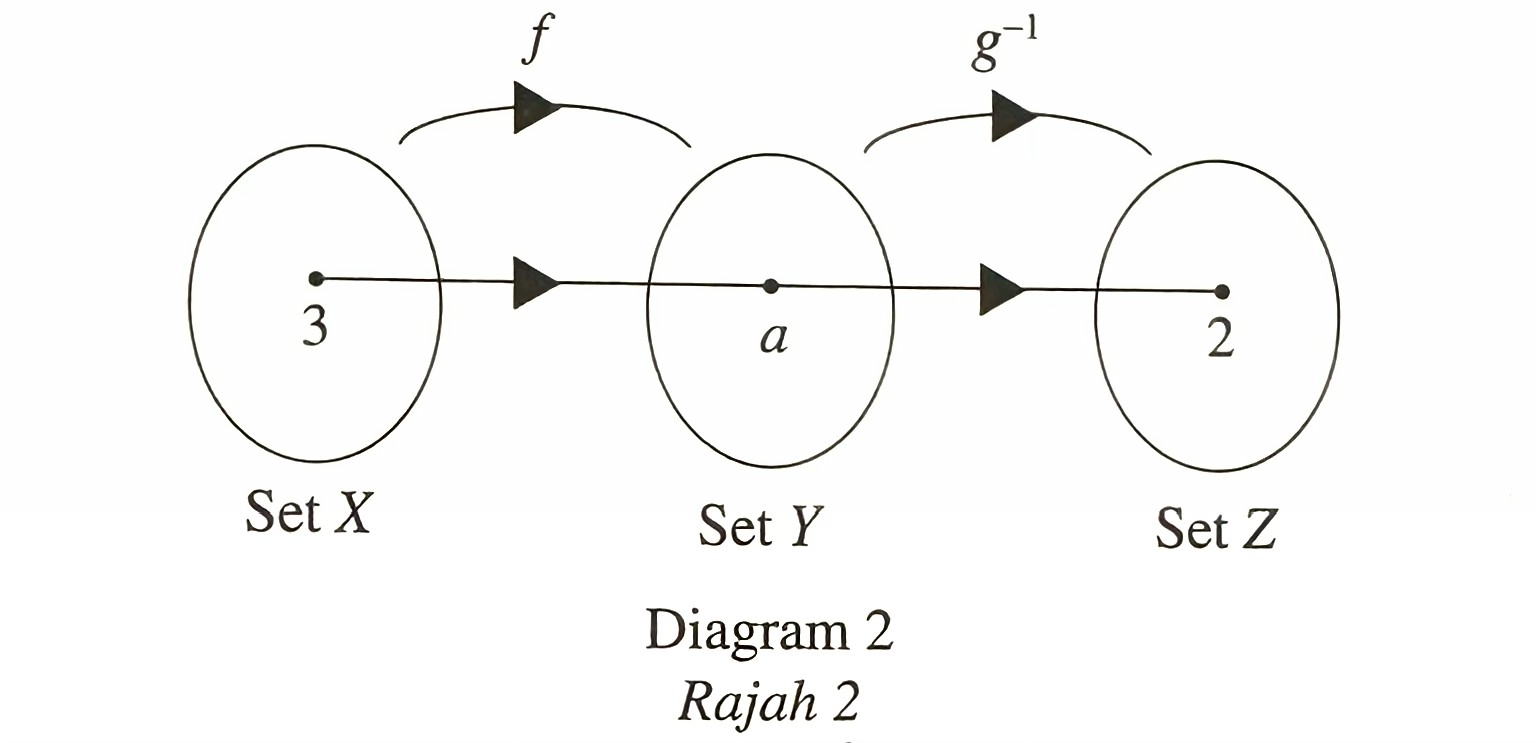
$$ \text { Diberi bahawa } f: x \rightarrow 2 x+3 \text { dan } g^{-1} f: x \rightarrow \frac{3}{x}+1, x \neq 0 \text {. } $$
(a) Jika seorang murid menulis a = 10, tentukan sama ada nilai itu betul atau salah. Beri sebab anda.
(b) Cari g-1(x).
[4 markah]
Penyelesaian:
(a)
$$ \begin{aligned} &\begin{aligned} & f(x)=2 x+3 \\ & f(3)=2(3)+3=9 \\ & f(3)=a=9 \end{aligned}\\ &\text { Nilai } a=10 \text { adalah salah. } \end{aligned} $$
(b)
$$ \begin{aligned} & g^{-1} f(x)=\frac{3}{x}+1 \\ & g^{-1}(2 x+3)=\frac{3}{x}+1 \\ & \text { Katakan } 2 x+3=u \\ & 2 x=u-3 \\ & x=\frac{u-3}{2} \\ & g^{-1}(u)=\frac{\frac{3}{u-3}}{2}+1 \\ & =\frac{6}{u-3}+1 \\ & g^{-1}(x)=\frac{6}{x-3}+1, x \neq 3 \end{aligned} $$
Rajah 2 menunjukkan hubungan bagi tiga set.

$$ \text { Diberi bahawa } f: x \rightarrow 2 x+3 \text { dan } g^{-1} f: x \rightarrow \frac{3}{x}+1, x \neq 0 \text {. } $$
(a) Jika seorang murid menulis a = 10, tentukan sama ada nilai itu betul atau salah. Beri sebab anda.
(b) Cari g-1(x).
[4 markah]
Penyelesaian:
(a)
$$ \begin{aligned} &\begin{aligned} & f(x)=2 x+3 \\ & f(3)=2(3)+3=9 \\ & f(3)=a=9 \end{aligned}\\ &\text { Nilai } a=10 \text { adalah salah. } \end{aligned} $$
(b)
$$ \begin{aligned} & g^{-1} f(x)=\frac{3}{x}+1 \\ & g^{-1}(2 x+3)=\frac{3}{x}+1 \\ & \text { Katakan } 2 x+3=u \\ & 2 x=u-3 \\ & x=\frac{u-3}{2} \\ & g^{-1}(u)=\frac{\frac{3}{u-3}}{2}+1 \\ & =\frac{6}{u-3}+1 \\ & g^{-1}(x)=\frac{6}{x-3}+1, x \neq 3 \end{aligned} $$