1.5.2 Fungsi, SPM Praktis (Kertas 1 Soalan 11 - 20)

Soalan 11 (Kaedah Bandingan):

Jika f : x \to \frac{m x - n}{x - 2}, x \neq 2 dan f^{- 1} : x \to \frac{5 - 2 x}{2 - x}, x \neq 2.

Cari nilai m dan n.

Penyelesaian:

\begin{array}{l} f (x) = \frac{m x - n}{x - 2} \\ Katakan y = \frac{m x - n}{x - 2} \to cari f^{- 1} (x) \\ y (x - 2) = m x - n \\ x y - 2 y = m x - n \\ x y - m x = 2 y - n \to \begin{array}{l} pindah x ke \\ sebelah kiri \end{array} \end{array}

\begin{array}{l} x (y - m) = 2 y - n \\ x = \frac{2 y - n}{y - m} \\ f^{- 1} (x) = \frac{2 x - n}{x - m} \\ \frac{2 x - n}{x - m} = \frac{5 - 2 x}{2 - x} \to \begin{array}{l} bandingkan dengan \\ f^{- 1} (x) yang diberi \end{array} \\ \times \frac{- 1}{- 1} \frac{n - 2 x}{m - x} = \frac{5 - 2 x}{2 - x} \\ maka, n = 5, m = 2 \end{array}

Soalan 12 (Kaedah Bandingan):

Diberi bahawa

f : x \to \frac{2 h}{x - 3 k}, x \neq 3 k,

dengan keadaan h dan k ialah pemalar dan

f^{- 1} : x \to \frac{14 + 24 x}{x}, x \neq 0.

Cari nilai h dan k.

Penyelesaian:

\begin{array}{l} f (x) = \frac{2 h}{x - 3 k} \\ Katakan y = \frac{2 h}{x - 3 k} \to cari f^{- 1} (x) \\ y (x - 3 k) = 2 h \\ x y - 3 k y = 2 h \\ x y = 2 h + 3 k y \\ x = \frac{2 h + 3 k y}{y} \end{array}

\begin{array}{l} f^{- 1} (x) = \frac{2 h + 3 k x}{x} \\ \frac{2 h + 3 k x}{x} = \frac{14 + 24 x}{x} \to \begin{array}{l} bandingkan dengan \\ f^{- 1} (x) yang diberi \end{array} \\ 2 h = 14 3 k = 24 \\ h = 7 k = 8 \end{array}

Soalan 13:
Diberi fungsi g(x) = 3x dan h(x) = m – nx, dengan keadaan m dan n ialah pemalar.
Ungkapkan m dalam sebutan n dengan keadaan hg(1) = 4.

Penyelesaian:

\begin{array}{l} h g (x) = h (3 x) \\ = m - n (3 x) \\ = m - 3 n x \\ h g (1) = 4 \\ m - 3 n (1) = 4 \\ m - 3 n = 4 \\ m = 4 + 3 n \end{array}

Soalan 14:
Diberi fungsi g : x → 3x – 2, cari
(a) nilai x apabila g(x) memeta kepada diri sendiri,
(b) nilai k dengan keadaan g(2 – k) = 4k.

Penyelesaian:
(a)

\begin{array}{l} g (x) = x \\ 3 x - 2 = x \\ 3 x - x = 2 \\ 2 x = 2 \\ x = 1 \end{array}

(b)

\begin{array}{l} g (x) = 3 x - 2 \\ g (2 - k) = 4 k \\ 3 (2 - k) - 2 = 4 k \\ 6 - 3 k - 2 = 4 k \\ - 7 k = - 4 \\ k = \frac{4}{7} \end{array}

Soalan 15:
Diberi fungsi f : x → px + 1, g : x → 3x – 5 dan fg(x) = 3px + q.
Ungkapkan p dalam sebutan q.

Penyelesaian:

\begin{array}{l} f (x) = p x + 1, g (x) = 3 x - 5 \\ f g (x) = p (3 x - 5) + 1 \\ = 3 p x - 5 p + 1 \\ Diberi f g (x) = 3 p x + q \\ 3 p x - 5 p + 1 = 3 p x + q \\ - 5 p + 1 = q \\ - 5 p = q - 1 \\ 5 p = 1 - q \\ p = \frac{1 - q}{5} \end{array}

Soalan 16:
Diberi fungsi h : x → 3x + 1, dan gh : x → 9x² + 6x – 4, cari
(a) h^-1 (x),
(b) g(x).

Penyelesaian:
(a)

\begin{array}{l} Katakan h^{- 1} (x) = y, \\ oleh itu h (y) = x \\ 3 y + 1 = x \\ 3 y = x - 1 \\ y = \frac{x - 1}{3} \\ ∴ h^{- 1} (x) = \frac{x - 1}{3} \\ h^{- 1} : x \mapsto \frac{x - 1}{3} \end{array}

(b)

\begin{array}{l} g [h (x)] = 9 x^{2} + 6 x - 4 \\ g (3 x + 1) = 9 x^{2} + 6 x - 4 \\ Katakan y = 3 x + 1 \\ oleh itu x = \frac{y - 1}{3} \\ g (y) = 9 {(\frac{y - 1}{3})}^{2} + 6 (\frac{y - 1}{3}) - 4 \\ = \frac{9 {(y - 1)}^{2}}{9} + 2 (y - 1) - 4 \\ = y^{2} - 2 y + 1 + 2 y - 2 - 4 \\ = y^{2} - 5 \\ ∴ g (x) = x^{2} - 5 \end{array}

Soalan 17:

Diberi bahawa fungsi f : x → 6x + 1. Cari nilai p jika f (4) = 4p + 5.

Penyelesaian:

f : x → 6x+ 1

f (x) = 6x + 1

f (4) = 6(4) + 1

f (4) = 25

f (4) = 4p + 5

25 = 4p + 5

4p = 25 – 5 = 20

p = 20/4 = 5

Soalan 18:

Diberi

g : x \to \frac{3 x - 5}{2 x + 7}

Fungsi g ditakrifkan untuk semua nilai x kecuali x = a. Cari niali a.

Penyelesaian:

Diingatkan bahawa g (x) tidak tertakrif jika penyebut = 0 iaitu [2x + 7 = 0]

2x + 7 = 0

2x = –7

x = - \frac{7}{2}

Apabila

x = - \frac{7}{2}

, g (x) tidak tertakrif

atau g (x) ditakrifkan untuk semua nilai x kecuali

x = - \frac{7}{2}, maka a = - \frac{7}{2}

Soalan 19:

Diberi bahawa fungsi f : x → 3x+ 2. Cari nilai

(a) f (2)

(b) f (– 5)

Penyelesaian:

Soalan 20:

Jika f : x → x² + 3x+ 2, ungkapkan setiap yang berikut dalam sebutan x:

(a) f (2x)

(b) f (3x+ 1)

Penyelesaian:

3 thoughts on “1.5.2 Fungsi, SPM Praktis (Kertas 1 Soalan 11 – 20)”

syakilayazid

March 6, 2018 at 12:36 pm | Reply

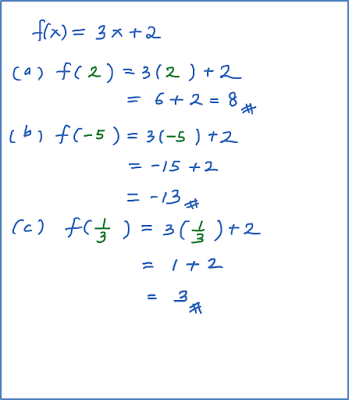
Tq a lot..I hope u can show alot of questions and answer…now i can do the best for my exam..
- nisha
  
  May 5, 2019 at 1:35 am | Reply
  
  its help me a lot … thanks….
nisha

May 5, 2019 at 1:33 am | Reply

thank you so much… its really help me to understand better

3 thoughts on “1.5.2 Fungsi, SPM Praktis (Kertas 1 Soalan 11 – 20)”

Leave a Comment Cancel reply