Kertas Model SPM Matematik Tambahan (Soalan dan Jawapan)

Kertas Model SPM Matematik Tambahan

Bahagian A

[40 markah]

Jawap semua soalan

Soalan 5

Rajah 2 menunjukkan sebuah segi tiga EFG.

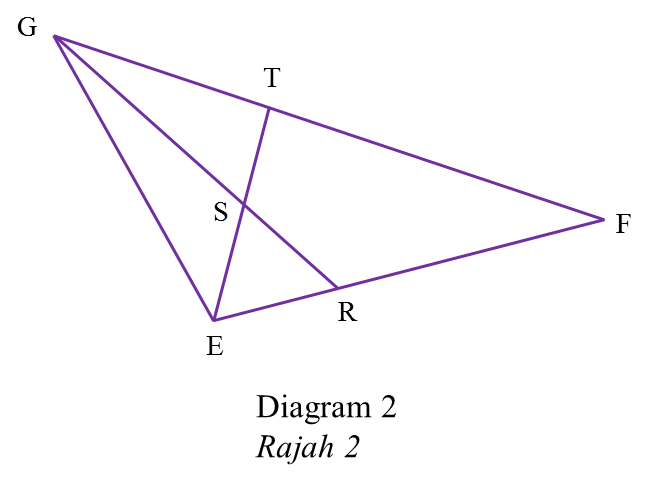
Diberi E R : R F = 1 : 2, F G : T G = 3 : 1, \vec{E R} = 4 \underset{˜}{x} dan \vec{E G} = 6 \underset{˜}{y} .

\begin{array}{l} (a) Ungkapkan dalam sebutan \underset{˜}{x} dan \underset{˜}{y} : \\ (i) \vec{G R} \\ (ii) \vec{G T} \end{array}

[3 markah]

(b) Jika garis GR diunjurkan ke titik K dengan keadaan

\vec{G K} = h \vec{G R} dan \vec{E K} = 6 \underset{˜}{x} - 3 \underset{˜}{y}, cari nilai bagi h .

[3 markah]

Jawapan serta penyelesaian:

(a)(i)

\begin{array}{l} \vec{G R} = \vec{G E} + \vec{E R} \\ = - 6 \underset{˜}{y} + 4 \underset{˜}{x} \end{array}

(a)(ii)

\begin{array}{l} \vec{G T} = \frac{1}{3} \vec{G F} \\ = \frac{1}{3} (\vec{G R} + \vec{R F}) \\ = \frac{1}{3} (- 6 \underset{˜}{y} + 4 \underset{˜}{x} + 8 \underset{˜}{x}) \leftarrow \vec{R F} = 2 \vec{E R} \\ = - 2 \underset{˜}{y} + 4 \underset{˜}{x} \end{array}

(b)

\begin{array}{l} \vec{G K} = h \vec{G R} \\ \vec{G E} + \vec{E K} = h \vec{G R} \\ - 6 \underset{˜}{y} + (6 \underset{˜}{x} - 3 \underset{˜}{y}) = h (- 6 \underset{˜}{y} + 4 \underset{˜}{x}) \\ - 9 \underset{˜}{y} + 6 \underset{˜}{x} = - 6 h \underset{˜}{y} + 4 h \underset{˜}{x} \\ Bandingkan, \\ - 6 h = - 9 \\ h = \frac{3}{2} \end{array}

Soalan 6

Penyelesaian secara lukisan berskala tidak diterima.

Rajah 3 menunjukkan tiga titik, A, B dan D pada satu satah Cartesan. Garis lurus AB berserenjang dengan garis lurus BD yang bersilang dengan paksi-y pada titik D. Persamaan garis lurus BD
ialah y = 2x – 5.

(a) Cari persamaan garis lurus AB. [2 Markah]

(b) Garis lurus AB dipanjangkan ke titik C dengan keadaan AB : BC = 2 : 3.
Cari koordinat titik C. [3 Markah]

(c) Titik P bergerak dengan keadaan jaraknya dari A adalah sama dengan jaraknya dari B.
Cari persamaan lokus P. [2 Markah]

Jawapan serta penyelesaian:

(a)

y= 2x – 5

m_BD= 2, m_AB= –½

y– 6 = –½ (x – 3)

2y – 12 = –x + 3

2y = –x+ 15

(b)

y= 2x – 5 ----- (1)

2y = –x + 15 ----- (2)

Gantikan (1) ke dalam (2),

2(2x – 5) = –x + 15

4x – 10 = –x + 15

5x = 25

x = 5

Apabila x = 5, Daripada (1)

y = 2(5) – 5 = 5

B = (5, 5)

AB: BC = 2 : 3

Katakan koordinat titik C = (h, k)

\begin{array}{l} (\frac{3 (3) + 2 h}{3 + 2}, \frac{3 (6) + 2 k}{3 + 2}) = (5, 5) \\ \frac{9 + 2 h}{5} = 5 atau \frac{18 + 2 k}{5} = 5 \\ 9 + 2 h = 25 18 + 2 k = 25 \\ h = 8 k = 3 \frac{1}{2} \\ Koordinat titik C = (8, 3 \frac{1}{2}) \end{array}

(c)

Katakan titik P= (x, y)

√(x – 3)²+ (y – 6)² = √(x – 5)² + (y – 5)²

(x – 3)²+ (y – 6)² = (x – 5)² + (y – 5)² ← (Kuasa dua kedua-dua belah)

x²– 6x + 9 + y² – 12y + 36 = x² – 10x + 25 + y² – 10y + 25

4x – 2y– 5 = 0

Leave a Comment Cancel reply