2.11.6 Fungsi Kuadratik, SPM Praktis (Soalan Panjang)

Soalan 11:


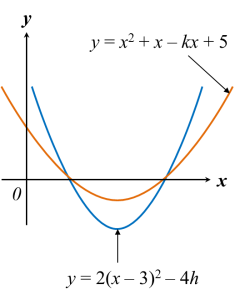
Rajah di atas menunjukkan graf lengkung y = x² + x – kx + 5 dan y = 2(x – 3) – 4h yang bersilang pada dua titik pada paksi-x. Cari
(a) nilai k dan nilai h,
(b) nilai minimum bagi kedua-dua lengkung itu.


Penyelesaian:
(a)
$\begin{array}{l}y=x^2+x-kx+5\\ =x^2+\left(1-k\right)x+5\\ ={\left[x+\frac{\left(1-k\right)}{2}\right]}^2-{\left(\frac{1-k}{2}\right)}^2+5\\ \text{paksi simetri bagi graf ini ialah}\\ x=-\frac{\left(1-k\right)}{2}\end{array}$

$\begin{array}{l}y=2{\left(x-3\right)}^2-4h\\ \text{paksi simetri bagi graf ini ialah}\\ x=3.\\ \text{Maka, }-\frac{1-k}{2}=3\\ -1+k=6\\ k=7\end{array}$

$\begin{array}{l}\text{Gantikan }k=7\text{ ke dalam persamaan}\\ y=x^2+x-7x+5\\ =x^2-6x+5\\ \text{Pada paksi}-x,y=0;\\ x^2-6x+5=0\\ \left(x-1\right)\left(x-5\right)=0\\ x=1,5\end{array}$

$\begin{array}{l}\text{Pada titik }\left(1,0\right)\\ \text{Gantikan }x=1,y=0\text{ ke dalam graf:}\\ y=2{\left(x-3\right)}^2-4h\\ 0=2{\left(1-3\right)}^2-4h\\ 4h=2\left(4\right)\\ 4h=8\\ h=2\end{array}$

(b)
$\begin{array}{l}\text{Lengkung }y=x^2-6x+5\\ ={\left(x-3\right)}^2-9+5\\ ={\left(x-3\right)}^2-4\\ \text{Maka, nilai minimumnya}=-4.\\ \\ \text{Bagi lengkung }y=2{\left(x-3\right)}^2-8,\text{ nilai minimum}=-8.\end{array}$

Soalan 12:
Fungsi kuadratik f(x) = x² – 4px + 5p² + 1 mempunyai nilai minimum m² + 2p, dengan keadaan m dan p adalah pemalar.
(a) Dengan menggunakan kaedah menyempurnakan kuasa dua, tunjukkan bahawa m = p – 1.
(b) Seterusnya, atau dengan cara lain, carikan nilai p dan nilai m jika graf bagi fungsi itu bersimetri pada x = m² – 1.

Penyelesaian:
(a)
$\begin{array}{l}f\left(x\right)=x^2-4px+5p^2+1\\ =x^2-4px+{\left(\frac{-4p}{2}\right)}^2-{\left(\frac{-4p}{2}\right)}^2+5p^2+1\\ ={\left(x-2p\right)}^2+p^2+1\\ \\ \text{Nilai minimum,}\\ m^2+2p=p^2+1\\ m^2=p^2-2p+1\\ m^2={\left(p-1\right)}^2\\ m=p-1\end{array}$

(b)
$\begin{array}{l}x=m^2-1\\ 2p=m^2-1\\ p=\frac{m^2-1}{2}\\ \text{Diberi }m=p-1\Rightarrow p=m+1\\ m+1=\frac{m^2-1}{2}\\ 2m+2=m^2-1\\ m^2-2m-3=0\\ \left(m-3\right)\left(m+1\right)=0\\ m=3\text{ atau }-1\\ \\ \text{Apabila }m=3,\\ p=\frac{3^2-1}{2}=4\end{array}$