Soalan 14:
Penyelesaian secara lakaran graf tidak diterima.
Zarah P bergerak di sepanjang suatu garis lurus dengan keadaan titik tetap A dan titik tetap B berada pada garis lurus itu. Halajunya, dalam m s-1, diberi oleh v = 3t2 + 4t – 15, dengan keadaan t ialah masa, dalam saat, selepas melalui titik A ke arah titik B.
[Anggapkan gerakan ke arah kanan sebagai positif]
(a) Tentukan sama ada titik A berada di kiri atau di kanan titik B. Justifikasikan jawapan anda.
[1 markah]
(b) Cari pecutan, dalam m s-2, zarah itu pada t = 1.3 s.
[2 markah]
(c) Jika jarak di antara titik A dan titik B ialah 15 m , tentukan sama ada zarah itu akan melalui titik B atau tidak. Beri satu sebab untuk jawapan anda.
[4 markah]
(d) Zarah Q bergerak di sepanjang garis lurus yang sama dengan keadaan halajunya, v = m s-1 , diberi oleh v = 2t2 – 7t + 6, dengan keadaan t ialah masa, dalam saat, selepas melalui titik A.
Tentukan julat masa, dalam saat, apabila kedua-dua zarah itu bergerak ke kiri.
[3 markah]
Jawapan:
(a)
$$ \text { Apabila } t=0, v=3(0)^2+4(0)-15 $$
$$ v=-15 \mathrm{~m} \mathrm{~s}^{-1} \text { (zarah bergerak ke kiri ) } $$
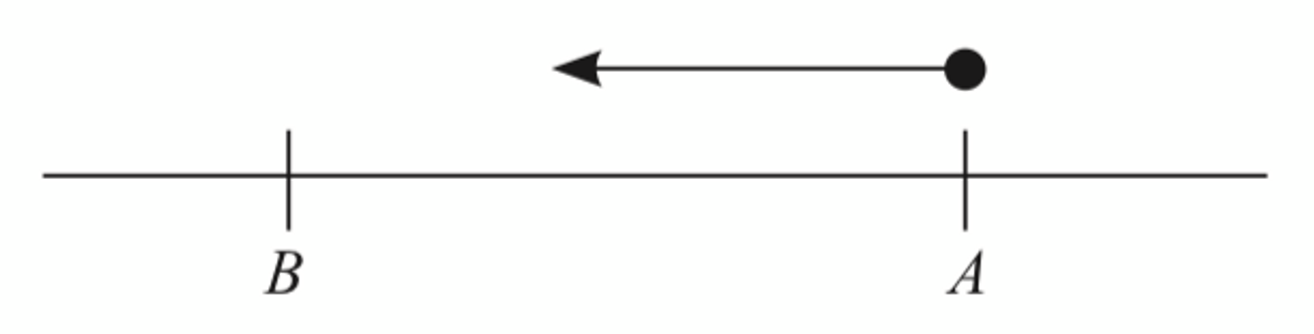
$$ \therefore \text { Titik } A \text { berada di kanan titik } B \text {. } $$
(b)
$$ \begin{aligned} & a=\frac{\mathrm{d} v}{\mathrm{~d} t} \\ & a=6 t+4 ; \text { apabila } t=1.3 \mathrm{~s} \\ & a=6(1.3)+4 \\ & a=11.8 \mathrm{~m} \mathrm{~s}^{-2} \end{aligned} $$
(c)
$$ \begin{aligned} &\text { Maksimum, } s \text {; }\\ &\begin{aligned} & \begin{aligned} v=0 \Rightarrow & 3 t^2+4 t-15=0 \\ & (3 t-5)(t+3)=0 \\ 3 t-5= & 0, t+3=0 \\ t= & \frac{5}{3}, t=-3(\text { abaikan } ) \end{aligned} \end{aligned} \end{aligned} $$
$$ \begin{aligned} & s=\int\left(3 t^2+4 t-15\right) \mathrm{d} t \\ & s=\frac{3 t^3}{3}+\frac{4 t^2}{2}-15 t+c \\ & s=t^3+2 t^2-15 t+c \end{aligned} $$
$$ \begin{aligned} & \text { Apabila } t=0, s=0 \text {; } \\ & 0=(0)^3+2(0)^2-15(0)+c \\ & 0=c \\ & \therefore s=t^3+2 t^2-15 t \end{aligned} $$
$$ \begin{aligned} & \text { Apabila } t=\frac{5}{3} \\ & s=\left(\frac{5}{3}\right)^3+2\left(\frac{5}{3}\right)^2-15\left(\frac{5}{3}\right) \\ & s=-14 \frac{22}{27} \mathrm{~m} \end{aligned} $$
Zarah P tidak akan melalui titik B kerana ia hanya boleh bergerak dengan jarak maksimum sejauh 14 22/27 m dari titik A, sedangkan titik B berada sejauh 15 m dari titik A.
(d)
$$ \text { Zarah bergerak ke kiri, } v<0 $$
$$ \begin{aligned} v_P & <0 \\ 3 t^2+4 t-15 & <0 \\ (3 t-5)(t+3) & <0 \end{aligned} $$
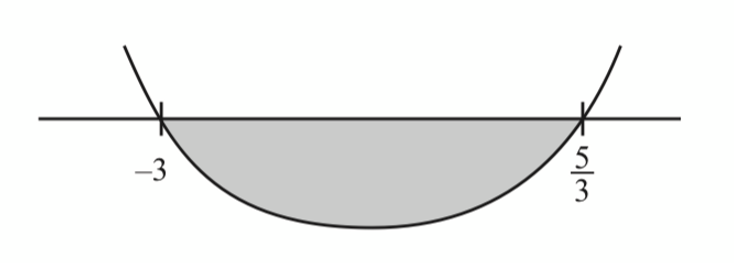$$
3<t<\frac{5}{3}
$$
$$ \begin{aligned} v_Q & <0 \\ 2 t^2-7 t+6 & <0 \\ (2 t-3)(t-2) & <0 \end{aligned} $$
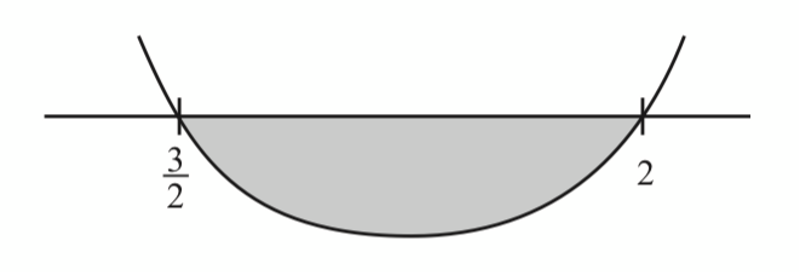$$
\frac{3}{2}<t<2
$$
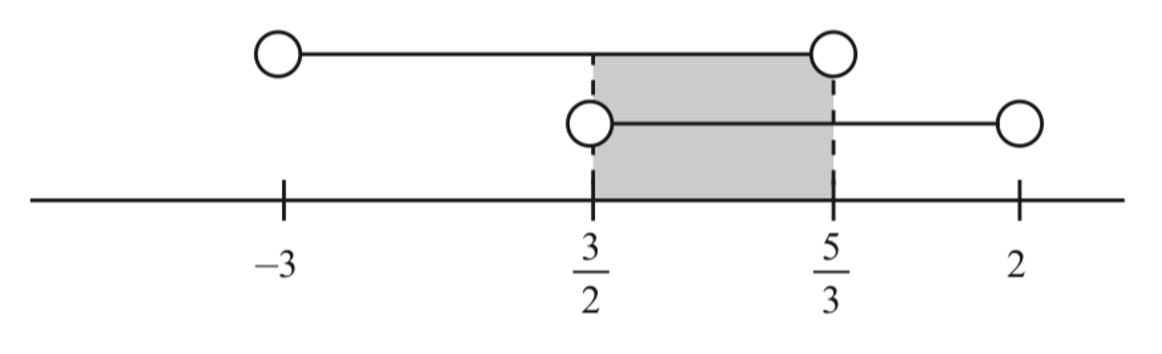$$
\text { Kedua-dua zarah bergerak ke kiri apabila } \frac{3}{2}<t<\frac{5}{3} \text {. }
$$
Penyelesaian secara lakaran graf tidak diterima.
Zarah P bergerak di sepanjang suatu garis lurus dengan keadaan titik tetap A dan titik tetap B berada pada garis lurus itu. Halajunya, dalam m s-1, diberi oleh v = 3t2 + 4t – 15, dengan keadaan t ialah masa, dalam saat, selepas melalui titik A ke arah titik B.
[Anggapkan gerakan ke arah kanan sebagai positif]
(a) Tentukan sama ada titik A berada di kiri atau di kanan titik B. Justifikasikan jawapan anda.
[1 markah]
(b) Cari pecutan, dalam m s-2, zarah itu pada t = 1.3 s.
[2 markah]
(c) Jika jarak di antara titik A dan titik B ialah 15 m , tentukan sama ada zarah itu akan melalui titik B atau tidak. Beri satu sebab untuk jawapan anda.
[4 markah]
(d) Zarah Q bergerak di sepanjang garis lurus yang sama dengan keadaan halajunya, v = m s-1 , diberi oleh v = 2t2 – 7t + 6, dengan keadaan t ialah masa, dalam saat, selepas melalui titik A.
Tentukan julat masa, dalam saat, apabila kedua-dua zarah itu bergerak ke kiri.
[3 markah]
Jawapan:
(a)
$$ \text { Apabila } t=0, v=3(0)^2+4(0)-15 $$
$$ v=-15 \mathrm{~m} \mathrm{~s}^{-1} \text { (zarah bergerak ke kiri ) } $$
$$ \therefore \text { Titik } A \text { berada di kanan titik } B \text {. } $$
(b)
$$ \begin{aligned} & a=\frac{\mathrm{d} v}{\mathrm{~d} t} \\ & a=6 t+4 ; \text { apabila } t=1.3 \mathrm{~s} \\ & a=6(1.3)+4 \\ & a=11.8 \mathrm{~m} \mathrm{~s}^{-2} \end{aligned} $$
(c)
$$ \begin{aligned} &\text { Maksimum, } s \text {; }\\ &\begin{aligned} & \begin{aligned} v=0 \Rightarrow & 3 t^2+4 t-15=0 \\ & (3 t-5)(t+3)=0 \\ 3 t-5= & 0, t+3=0 \\ t= & \frac{5}{3}, t=-3(\text { abaikan } ) \end{aligned} \end{aligned} \end{aligned} $$
$$ \begin{aligned} & s=\int\left(3 t^2+4 t-15\right) \mathrm{d} t \\ & s=\frac{3 t^3}{3}+\frac{4 t^2}{2}-15 t+c \\ & s=t^3+2 t^2-15 t+c \end{aligned} $$
$$ \begin{aligned} & \text { Apabila } t=0, s=0 \text {; } \\ & 0=(0)^3+2(0)^2-15(0)+c \\ & 0=c \\ & \therefore s=t^3+2 t^2-15 t \end{aligned} $$
$$ \begin{aligned} & \text { Apabila } t=\frac{5}{3} \\ & s=\left(\frac{5}{3}\right)^3+2\left(\frac{5}{3}\right)^2-15\left(\frac{5}{3}\right) \\ & s=-14 \frac{22}{27} \mathrm{~m} \end{aligned} $$
Zarah P tidak akan melalui titik B kerana ia hanya boleh bergerak dengan jarak maksimum sejauh 14 22/27 m dari titik A, sedangkan titik B berada sejauh 15 m dari titik A.
(d)
$$ \text { Zarah bergerak ke kiri, } v<0 $$
$$ \begin{aligned} v_P & <0 \\ 3 t^2+4 t-15 & <0 \\ (3 t-5)(t+3) & <0 \end{aligned} $$
$$
3<t<\frac{5}{3}
$$$$ \begin{aligned} v_Q & <0 \\ 2 t^2-7 t+6 & <0 \\ (2 t-3)(t-2) & <0 \end{aligned} $$
$$
\frac{3}{2}<t<2
$$$$
\text { Kedua-dua zarah bergerak ke kiri apabila } \frac{3}{2}<t<\frac{5}{3} \text {. }
$$