Soalan 13:
Mus ingin menjual dua jenis kerepek. Jadual 3 menunjukkan maklumat berkaitan dua jenis kerepek itu.
(a) Mus mempunyai RM125 untuk membeli kedua-dua jenis kerepek itu.
Tulis satu ketaksamaan untuk mewakili kekangan ini.
[1 markah]
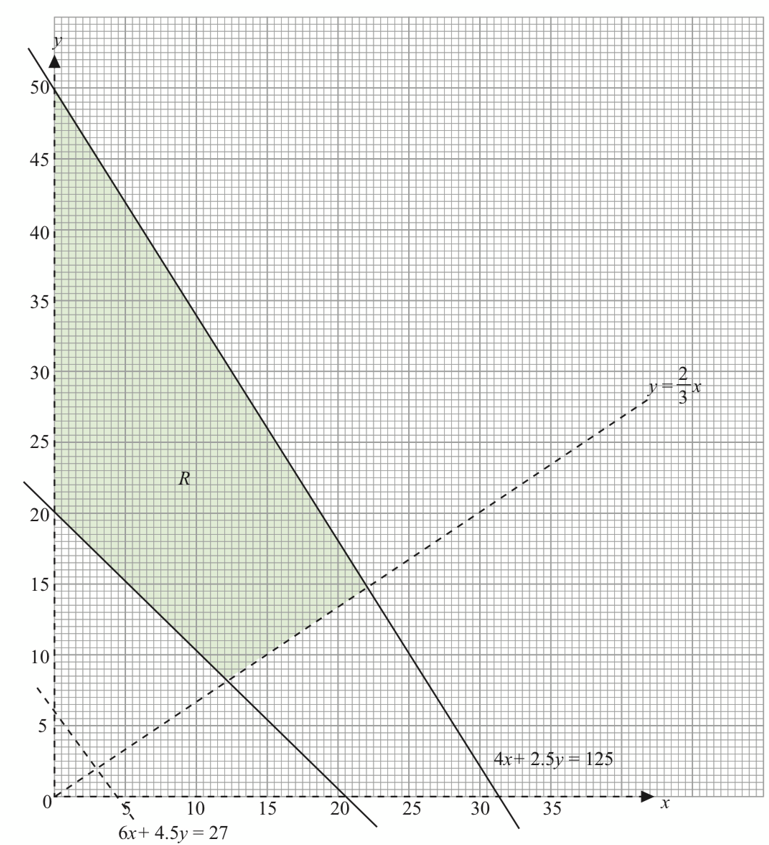
(b) Rantau berlorek dalam graf pada halaman 150 mewakili kekangan kedua.
Tulis satu ketaksamaan untuk mewakili kekangan itu.
[1 markah]
(c) Bilangan bungkus kerepek P yang dijual adalah kurang daripada 3/2 bilangan bungkus kerepek Q yang dijual.
Pada halaman 150, bina dan label rantau R yang memenuhi semua kekangan itu dan x > 0, y > 0.
[3 markah]
(d) Gunakan graf yang dibina di (c) untuk menjawab soalan-soalan berikut:
(i) Nyatakan bilangan maksimum bungkus kerepek P yang dijual jika 12 bungkus kerepek Q telah dijual.
(ii) Mus bercadang menyimpan 50% daripada jumlah keuntungan jualan. Dia juga perlu membayar upah seorang pekerja sebanyak RM40 daripada bakinya.
Dengan melukis garis fungsi objektif untuk mencari keuntungan yang diperoleh, tentukan sama ada harga jualan yang ditetapkan itu sesuai atau tidak. Beri justifikasi anda.
[Anda boleh menganggap bahawa dia menjual semua kerepek yang dibelinya.]
[5 markah]
Jawapan:
(a)
$$ 4 x+2.5 y \leqslant 125 $$
(b)
$$ \begin{aligned} & y=\frac{20-0}{0-20} x+20 \\ & y=-x+20 \\ & y \geqslant 20-x \end{aligned} $$
(c)
$$ \begin{aligned} & x<\frac{3}{2} y \\ & y>\frac{2}{3} x \end{aligned} $$
(d)(i) 17 bungkus
(d)(ii)
$$ \begin{aligned} \text { Untung, } P & =(10-4) x+(7-2.5) y \\ & =6 x+4.5 y \end{aligned} $$
$$ \text { Katakan } 6 x+4.5 y=27 $$
$$ \text { Titik optimum: }(0,50) $$
$$ \begin{aligned} P & =6(0)+4.5(50) \\ & =\text { RM } 225 \end{aligned} $$
$$ \begin{aligned} \text { Simpanan } & =50 \% \times \text { RM225 } \\ & =\text { RM112.50 } \end{aligned} $$
$$ \begin{aligned} \text { Baki } & =\text { RM112.50 }- \text { RM40 } \\ & =\text { RM72.50 } \end{aligned} $$
∴ Ya, harga jualan adalah sesuai kerana Mus boleh menyimpan duit dan membayar upah pekerja dan masih mempunyai baki sebanyak RM72.50 untuk modal seterusnya.
Mus ingin menjual dua jenis kerepek. Jadual 3 menunjukkan maklumat berkaitan dua jenis kerepek itu.
(a) Mus mempunyai RM125 untuk membeli kedua-dua jenis kerepek itu.Tulis satu ketaksamaan untuk mewakili kekangan ini.
[1 markah]
(b) Rantau berlorek dalam graf pada halaman 150 mewakili kekangan kedua.
Tulis satu ketaksamaan untuk mewakili kekangan itu.
[1 markah]
(c) Bilangan bungkus kerepek P yang dijual adalah kurang daripada 3/2 bilangan bungkus kerepek Q yang dijual.
Pada halaman 150, bina dan label rantau R yang memenuhi semua kekangan itu dan x > 0, y > 0.
[3 markah]
(d) Gunakan graf yang dibina di (c) untuk menjawab soalan-soalan berikut:
(i) Nyatakan bilangan maksimum bungkus kerepek P yang dijual jika 12 bungkus kerepek Q telah dijual.
(ii) Mus bercadang menyimpan 50% daripada jumlah keuntungan jualan. Dia juga perlu membayar upah seorang pekerja sebanyak RM40 daripada bakinya.
Dengan melukis garis fungsi objektif untuk mencari keuntungan yang diperoleh, tentukan sama ada harga jualan yang ditetapkan itu sesuai atau tidak. Beri justifikasi anda.
[Anda boleh menganggap bahawa dia menjual semua kerepek yang dibelinya.]
[5 markah]
Jawapan:
(a)
$$ 4 x+2.5 y \leqslant 125 $$
(b)
$$ \begin{aligned} & y=\frac{20-0}{0-20} x+20 \\ & y=-x+20 \\ & y \geqslant 20-x \end{aligned} $$
(c)
$$ \begin{aligned} & x<\frac{3}{2} y \\ & y>\frac{2}{3} x \end{aligned} $$
(d)(i) 17 bungkus
(d)(ii)
$$ \begin{aligned} \text { Untung, } P & =(10-4) x+(7-2.5) y \\ & =6 x+4.5 y \end{aligned} $$
$$ \text { Katakan } 6 x+4.5 y=27 $$
$$ \text { Titik optimum: }(0,50) $$
$$ \begin{aligned} P & =6(0)+4.5(50) \\ & =\text { RM } 225 \end{aligned} $$
$$ \begin{aligned} \text { Simpanan } & =50 \% \times \text { RM225 } \\ & =\text { RM112.50 } \end{aligned} $$
$$ \begin{aligned} \text { Baki } & =\text { RM112.50 }- \text { RM40 } \\ & =\text { RM72.50 } \end{aligned} $$
∴ Ya, harga jualan adalah sesuai kerana Mus boleh menyimpan duit dan membayar upah pekerja dan masih mempunyai baki sebanyak RM72.50 untuk modal seterusnya.