Soalan 15:
Jadual 4 menunjukkan maklumat bagi empat jenis bahan yang digunakan untuk menghasilkan sejenis biskut.
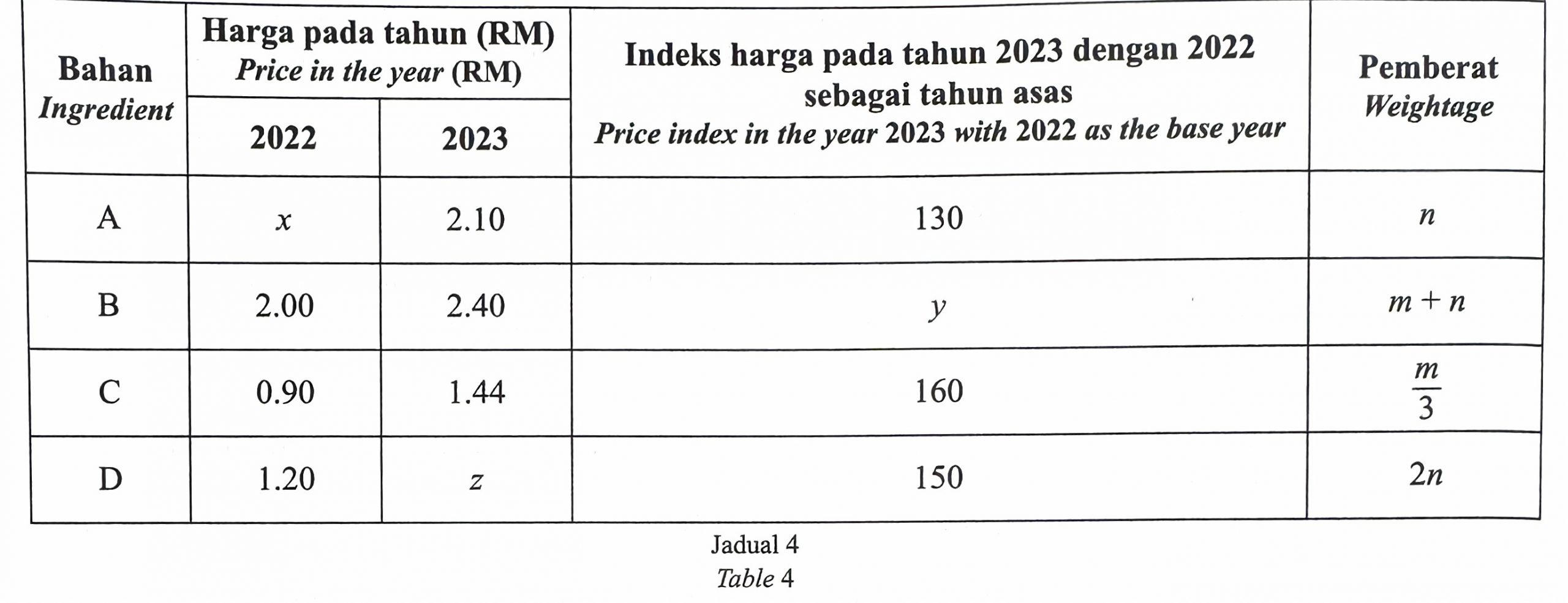
(a) Cari nilai x, nilai y dan nilai z.
[3 markah]
(b) Indeks gubahan bagi kos penghasilan biskut itu pada tahun 2023 dengan 2022 sebagai tahun asas ialah 135.
(i) Cari nisbah bahan A kepada bahan B yang digunakan.
(ii) Kos penghasilan 200 biji biskut pada tahun 2022 ialah RM25. Harga setiap bahan dijangka meningkat sebanyak 20.25% dari tahun 2023 ke tahun 2025. Pada tahun 2025, bekas yang digunakan untuk memuatkan 40 biji biskut dijangkakan berharga RM1.50 seunit.
Pada tahun 2025, jika RM45 diperuntukkan untuk menghasilkan 200 biji biskut termasuk pembelian bekas itu, tentukan sama ada peruntukan itu mencukupi atau tidak.
[7 markah]
Jawapan:
(a)
$$ \begin{aligned} \bar{I}_{\frac{23}{22}} & =130 \\ \frac{2.10}{x} \times 100 & =130 \\ \frac{2.10}{x} & =\frac{130}{100} \\ x & =\frac{2.10 \times 100}{130} \\ x & =1.62 \end{aligned} $$
$$ \begin{aligned} & y=\frac{2.40}{2.00} \times 100 \\ & y=120 \end{aligned} $$
$$ \begin{aligned} \bar{I}_{\frac{23}{22}} & =150 \\ \frac{z}{1.20} \times 100 & =150 \\ z & =\frac{150 \times 1.20}{100} \\ z & =1.80 \end{aligned} $$
(b)(i)
$$ \begin{aligned} \bar{I}_{\frac{23}{22}}=135 & \\ \frac{(130)(n)+(120)(m+n)+(160)\left(\frac{m}{3}\right)+(150)(2 n)}{n+m+n+\frac{m}{3}+2 n} & =135 \\ \frac{130 n+120 m+120 n+\frac{160}{3} m+300 n}{4 n+\frac{4}{3} m} & =135 \end{aligned} $$
$$ \begin{aligned} 550 n+\frac{520}{3} m & =135\left(4 n+\frac{4}{3} m\right) \\ 550 n+\frac{520}{3} m & =540 n+180 m \\ 550 n-540 n & =180 m-\frac{520}{3} m \\ 10 n & =\frac{20}{3} m \\ \frac{10}{\frac{20}{3}} & =\frac{m}{n} \\ \frac{3}{2} & =\frac{m}{n} \end{aligned} $$
$$ \therefore m: n=3: 2 $$
$$ \begin{aligned} & A: B=n: m+n \\ & A: B=2: 3+2 \\ & A: B=2: 5 \end{aligned} $$
(b)(ii)
$$ \begin{aligned} \bar{I}_{23 / 22} & =135 \\ \frac{P_{2023}}{P_{2022}} \times 100 & =135 \\ \frac{P_{2023}}{\mathrm{RM} 25} \times 100 & =135 \\ P_{2023} & =\frac{135 \times \mathrm{RM} 25}{100} \\ P_{2023} & =\mathrm{RM} 33.75 \end{aligned} $$
$$ \begin{aligned} \bar{I}_{25 / 23} & =100+20.25 \\ \frac{P_{2025}}{P_{2023}} \times 100 & =120.25 \\ \frac{P_{2025}}{\text { RM33.75 }} \times 100 & =120.25 \\ P_{2025} & =\frac{120.25 \times \text { RM33.75 }}{100} \\ P_{2025} & =\text { RM40.58 } \end{aligned} $$
$$ \begin{aligned} \text { Bilangan kotak } & =200 \div 40 \\ & =5 \end{aligned} $$
$$ \begin{aligned} \text { Harga kotak } & =5 \times \text { RM1.50 } \\ & =\text { RM7.50 } \end{aligned} $$
$$ \begin{aligned} &\text { Jumlah kos pada tahun } 2025 \\ &\begin{aligned} & =\text { RM40.58 }+ \text { RM7.50 } \\ & =\text { RM48.08 } \end{aligned} \end{aligned} $$
$$ \begin{aligned} &\text { RM48.08 > RM45 }\\ &\therefore \text { Duit yang diperuntukkan adalah tidak mencukupi. } \end{aligned} $$
Jadual 4 menunjukkan maklumat bagi empat jenis bahan yang digunakan untuk menghasilkan sejenis biskut.

(a) Cari nilai x, nilai y dan nilai z.
[3 markah]
(b) Indeks gubahan bagi kos penghasilan biskut itu pada tahun 2023 dengan 2022 sebagai tahun asas ialah 135.
(i) Cari nisbah bahan A kepada bahan B yang digunakan.
(ii) Kos penghasilan 200 biji biskut pada tahun 2022 ialah RM25. Harga setiap bahan dijangka meningkat sebanyak 20.25% dari tahun 2023 ke tahun 2025. Pada tahun 2025, bekas yang digunakan untuk memuatkan 40 biji biskut dijangkakan berharga RM1.50 seunit.
Pada tahun 2025, jika RM45 diperuntukkan untuk menghasilkan 200 biji biskut termasuk pembelian bekas itu, tentukan sama ada peruntukan itu mencukupi atau tidak.
[7 markah]
Jawapan:
(a)
$$ \begin{aligned} \bar{I}_{\frac{23}{22}} & =130 \\ \frac{2.10}{x} \times 100 & =130 \\ \frac{2.10}{x} & =\frac{130}{100} \\ x & =\frac{2.10 \times 100}{130} \\ x & =1.62 \end{aligned} $$
$$ \begin{aligned} & y=\frac{2.40}{2.00} \times 100 \\ & y=120 \end{aligned} $$
$$ \begin{aligned} \bar{I}_{\frac{23}{22}} & =150 \\ \frac{z}{1.20} \times 100 & =150 \\ z & =\frac{150 \times 1.20}{100} \\ z & =1.80 \end{aligned} $$
(b)(i)
$$ \begin{aligned} \bar{I}_{\frac{23}{22}}=135 & \\ \frac{(130)(n)+(120)(m+n)+(160)\left(\frac{m}{3}\right)+(150)(2 n)}{n+m+n+\frac{m}{3}+2 n} & =135 \\ \frac{130 n+120 m+120 n+\frac{160}{3} m+300 n}{4 n+\frac{4}{3} m} & =135 \end{aligned} $$
$$ \begin{aligned} 550 n+\frac{520}{3} m & =135\left(4 n+\frac{4}{3} m\right) \\ 550 n+\frac{520}{3} m & =540 n+180 m \\ 550 n-540 n & =180 m-\frac{520}{3} m \\ 10 n & =\frac{20}{3} m \\ \frac{10}{\frac{20}{3}} & =\frac{m}{n} \\ \frac{3}{2} & =\frac{m}{n} \end{aligned} $$
$$ \therefore m: n=3: 2 $$
$$ \begin{aligned} & A: B=n: m+n \\ & A: B=2: 3+2 \\ & A: B=2: 5 \end{aligned} $$
(b)(ii)
$$ \begin{aligned} \bar{I}_{23 / 22} & =135 \\ \frac{P_{2023}}{P_{2022}} \times 100 & =135 \\ \frac{P_{2023}}{\mathrm{RM} 25} \times 100 & =135 \\ P_{2023} & =\frac{135 \times \mathrm{RM} 25}{100} \\ P_{2023} & =\mathrm{RM} 33.75 \end{aligned} $$
$$ \begin{aligned} \bar{I}_{25 / 23} & =100+20.25 \\ \frac{P_{2025}}{P_{2023}} \times 100 & =120.25 \\ \frac{P_{2025}}{\text { RM33.75 }} \times 100 & =120.25 \\ P_{2025} & =\frac{120.25 \times \text { RM33.75 }}{100} \\ P_{2025} & =\text { RM40.58 } \end{aligned} $$
$$ \begin{aligned} \text { Bilangan kotak } & =200 \div 40 \\ & =5 \end{aligned} $$
$$ \begin{aligned} \text { Harga kotak } & =5 \times \text { RM1.50 } \\ & =\text { RM7.50 } \end{aligned} $$
$$ \begin{aligned} &\text { Jumlah kos pada tahun } 2025 \\ &\begin{aligned} & =\text { RM40.58 }+ \text { RM7.50 } \\ & =\text { RM48.08 } \end{aligned} \end{aligned} $$
$$ \begin{aligned} &\text { RM48.08 > RM45 }\\ &\therefore \text { Duit yang diperuntukkan adalah tidak mencukupi. } \end{aligned} $$