Soalan 5:
Suatu lengkung mempunyai fungsi kecerunan, dy/dx = 4x – 6 dan melalui P(1, 4).
(a) Cari persamaan lengkung itu. [3 markah]
(b) Normal kepada lengkung pada titik P menyilang lengkung sekali lagi pada titik Q. Cari koordinat Q. [4 markah]
Jawapan:
(a)
$$ \begin{aligned} & y=\int(4 x-6) \mathrm{d} x \\ & y=\frac{4 x^2}{2}-6 x+c \\ & y=2 x^2-6 x+c, \text { melalui } \text { }(1,4) \\ & 4=2(1)^2-(6) 1+c \\ & 4=-4+c \\ & c=4+4 \\ & c=8 \\ & \therefore y=2 x^2-6 x+8 \end{aligned} $$
(b)
$$ \begin{aligned} & m_{\text {tangen } \text { }}: \frac{\mathrm{d} y}{\mathrm{~d} x}=4 x-6 \text { pada } \text { }(1, 4) \\ & \frac{\mathrm{d} y}{\mathrm{~d} x}=4(1)-6 \\ & \quad=-2 \\ & m_{\text {normal }} \times m_{\text {tangen } \text { }}=-1 \\ & \quad m_{\text {normal }} \times-2=-1 \\ & \quad m_{\text {normal }}=\frac{1}{2} \end{aligned} $$ Persamaan normal melalui P(1, 4) : $$ \begin{aligned} y-y_1 & =m\left(x-x_1\right) \\ y-4 & =\frac{1}{2}(x-1) \\ y & =\frac{1}{2} x-\frac{1}{2}+4 \end{aligned} $$
$$ \begin{aligned} & y=\frac{1}{2} x+\frac{7}{2} \\ y= & 2 x^2-6 x+8 \ldots \text { (1) }\\ y= & \frac{1}{2} x+\frac{7}{2} \ldots \text { (2) } \end{aligned} $$
$$ \begin{aligned} &\text { (1) }=\text { (2) ; }\\ &\begin{aligned} 2 x^2-6 x+8 & =\frac{1}{2} x+\frac{7}{2} \\ 2 x^2-6 x-\frac{1}{2} x+8-\frac{7}{2} & =0 \\ 2 x^2-\frac{13}{2} x+\frac{9}{2} & =0 \\ 4 x^2-13 x+9 & =0 \\ (4 x-9)(x-1) & =0 \\ 4 x-9=0, x-1=0 & \\ x=\frac{9}{4}, & x=1 \text { (abaikan) } \end{aligned} \end{aligned} $$
$$ \begin{aligned} &\text { Dari (2), }\\ &\begin{aligned} & y=\frac{1}{2} x+\frac{7}{2} \\ & y=\frac{1}{2}\left(\frac{9}{4}\right)+\frac{7}{2} \\ & y=\frac{37}{8} \\ & \therefore Q\left(\frac{9}{4}, \frac{37}{8}\right) \end{aligned} \end{aligned} $$
Suatu lengkung mempunyai fungsi kecerunan, dy/dx = 4x – 6 dan melalui P(1, 4).
(a) Cari persamaan lengkung itu. [3 markah]
(b) Normal kepada lengkung pada titik P menyilang lengkung sekali lagi pada titik Q. Cari koordinat Q. [4 markah]
Jawapan:
(a)
$$ \begin{aligned} & y=\int(4 x-6) \mathrm{d} x \\ & y=\frac{4 x^2}{2}-6 x+c \\ & y=2 x^2-6 x+c, \text { melalui } \text { }(1,4) \\ & 4=2(1)^2-(6) 1+c \\ & 4=-4+c \\ & c=4+4 \\ & c=8 \\ & \therefore y=2 x^2-6 x+8 \end{aligned} $$
(b)
$$ \begin{aligned} & m_{\text {tangen } \text { }}: \frac{\mathrm{d} y}{\mathrm{~d} x}=4 x-6 \text { pada } \text { }(1, 4) \\ & \frac{\mathrm{d} y}{\mathrm{~d} x}=4(1)-6 \\ & \quad=-2 \\ & m_{\text {normal }} \times m_{\text {tangen } \text { }}=-1 \\ & \quad m_{\text {normal }} \times-2=-1 \\ & \quad m_{\text {normal }}=\frac{1}{2} \end{aligned} $$ Persamaan normal melalui P(1, 4) : $$ \begin{aligned} y-y_1 & =m\left(x-x_1\right) \\ y-4 & =\frac{1}{2}(x-1) \\ y & =\frac{1}{2} x-\frac{1}{2}+4 \end{aligned} $$
$$ \begin{aligned} & y=\frac{1}{2} x+\frac{7}{2} \\ y= & 2 x^2-6 x+8 \ldots \text { (1) }\\ y= & \frac{1}{2} x+\frac{7}{2} \ldots \text { (2) } \end{aligned} $$
$$ \begin{aligned} &\text { (1) }=\text { (2) ; }\\ &\begin{aligned} 2 x^2-6 x+8 & =\frac{1}{2} x+\frac{7}{2} \\ 2 x^2-6 x-\frac{1}{2} x+8-\frac{7}{2} & =0 \\ 2 x^2-\frac{13}{2} x+\frac{9}{2} & =0 \\ 4 x^2-13 x+9 & =0 \\ (4 x-9)(x-1) & =0 \\ 4 x-9=0, x-1=0 & \\ x=\frac{9}{4}, & x=1 \text { (abaikan) } \end{aligned} \end{aligned} $$
$$ \begin{aligned} &\text { Dari (2), }\\ &\begin{aligned} & y=\frac{1}{2} x+\frac{7}{2} \\ & y=\frac{1}{2}\left(\frac{9}{4}\right)+\frac{7}{2} \\ & y=\frac{37}{8} \\ & \therefore Q\left(\frac{9}{4}, \frac{37}{8}\right) \end{aligned} \end{aligned} $$
Soalan 6:
Jadual 1 menunjukkan kategori bagi indeks jisim tubuh untuk sekumpulan pekerja lelaki sebuah syarikat. Indeks jisim tubuh itu bertabur secara normal.

Diberi bahawa 44% pekerja itu dikategorikan sama ada berat normal atau kurang berat manakala 12% dikategorikan obes. Didapati bahawa, 1 daripada n pekerja berada dalam kategori kurang berat.
Cari nilai n.
[6 markah]
Jawapan:
$$ \begin{aligned} P(x<25) & =44 \% \\ P\left(Z<\frac{25-\mu}{\sigma}\right) & =0.44 \\ \frac{25-\mu}{\sigma} & =-0.151 \\ 25-\mu & =-0.151 \sigma \ldots(1) \end{aligned} $$
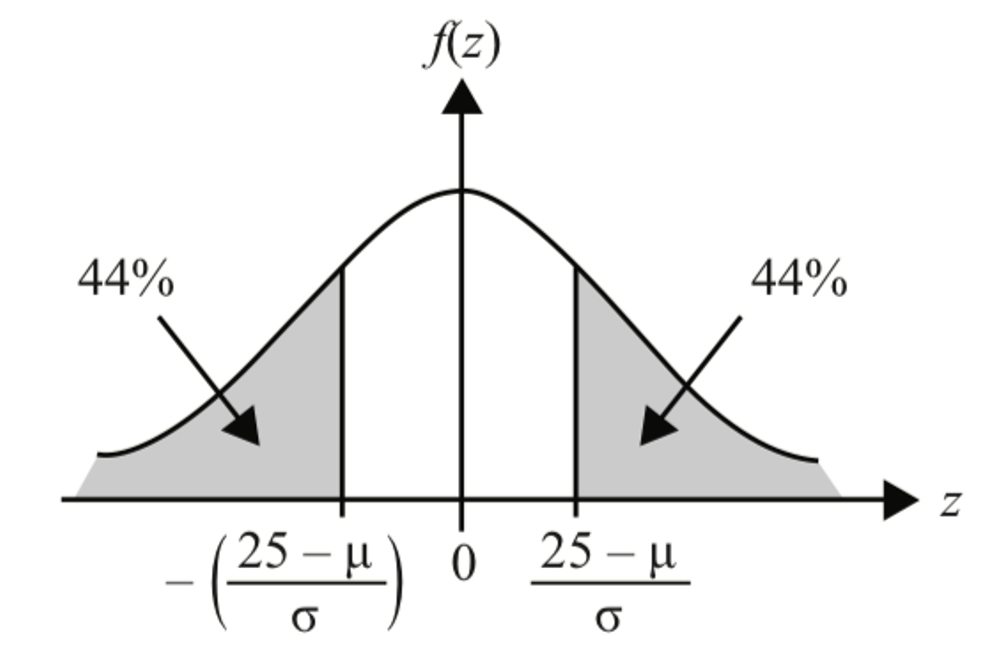
$$ \begin{aligned} P(x \geqslant 30) & =12 \% \\ P\left(Z>\frac{30-\mu}{\sigma}\right) & =0.12 \\ \frac{30-\mu}{\sigma} & =1.175 \\ 30-\mu & =1.175 \sigma \ldots(2) \end{aligned} $$
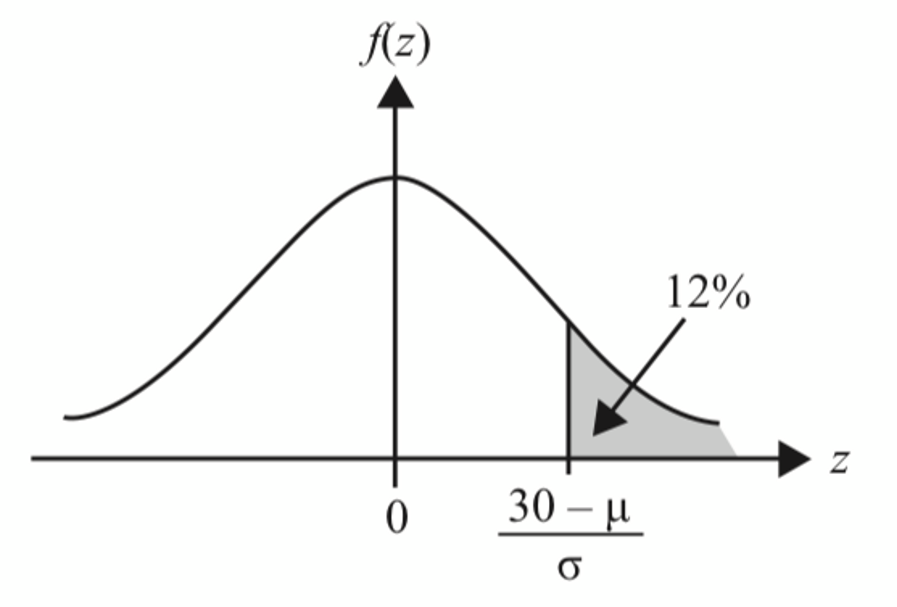
$$ \begin{aligned} &\text { (2) – (1); }\\ &\begin{aligned} (30-\mu)-(25-\mu) & =1.175 \sigma-(-0.151 \sigma) \\ 30-\mu-25+\mu & =1.175 \sigma+0.151 \sigma \\ 5 & =1.326 \sigma \\ \frac{5}{1.326} & =\sigma \\ \sigma & =3.7707 \end{aligned} \end{aligned} $$
$$ \begin{aligned} &\text { Dari (1), }\\ &\begin{aligned} 25-\mu & =-0.151 \sigma \\ 25-\mu & =-0.151(3.7707) \\ -\mu & =-0.5694-25 \\ -\mu & =-25.5694 \\ \mu & =25.5694 \end{aligned} \end{aligned} $$
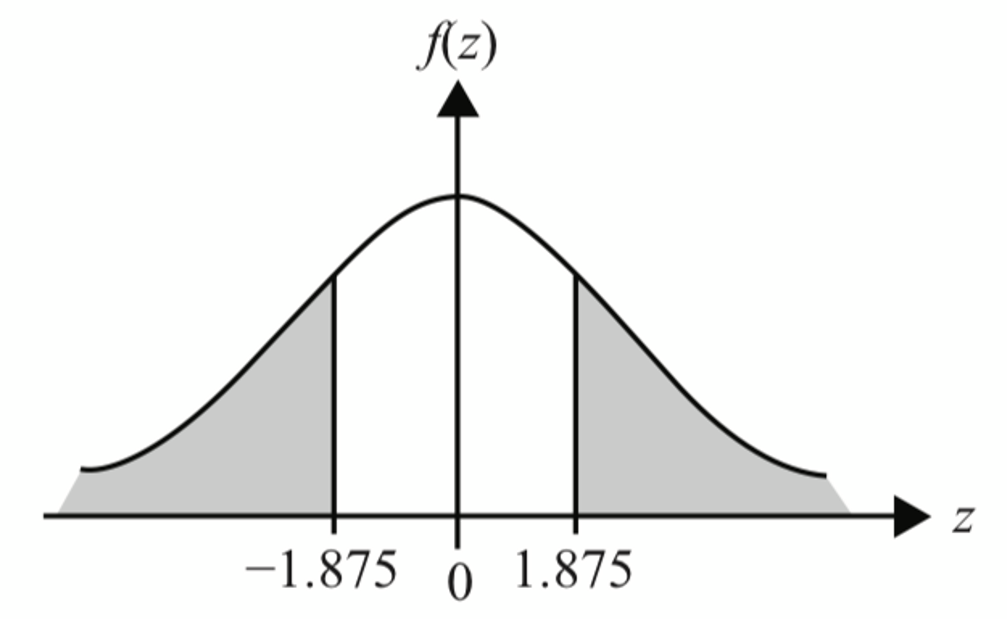
$$ \begin{aligned} P(X<18.5) & =\frac{1}{n} \\ P\left(Z<\frac{18.5-25.57}{3.77}\right) & =\frac{1}{n} \\ P(Z<-1.875) & =\frac{1}{n} \\ 0.0303 & =\frac{1}{n} \\ n & =\frac{1}{0.0303} \\ n & =33 \end{aligned} $$
Jadual 1 menunjukkan kategori bagi indeks jisim tubuh untuk sekumpulan pekerja lelaki sebuah syarikat. Indeks jisim tubuh itu bertabur secara normal.

Diberi bahawa 44% pekerja itu dikategorikan sama ada berat normal atau kurang berat manakala 12% dikategorikan obes. Didapati bahawa, 1 daripada n pekerja berada dalam kategori kurang berat.
Cari nilai n.
[6 markah]
Jawapan:
$$ \begin{aligned} P(x<25) & =44 \% \\ P\left(Z<\frac{25-\mu}{\sigma}\right) & =0.44 \\ \frac{25-\mu}{\sigma} & =-0.151 \\ 25-\mu & =-0.151 \sigma \ldots(1) \end{aligned} $$

$$ \begin{aligned} P(x \geqslant 30) & =12 \% \\ P\left(Z>\frac{30-\mu}{\sigma}\right) & =0.12 \\ \frac{30-\mu}{\sigma} & =1.175 \\ 30-\mu & =1.175 \sigma \ldots(2) \end{aligned} $$

$$ \begin{aligned} &\text { (2) – (1); }\\ &\begin{aligned} (30-\mu)-(25-\mu) & =1.175 \sigma-(-0.151 \sigma) \\ 30-\mu-25+\mu & =1.175 \sigma+0.151 \sigma \\ 5 & =1.326 \sigma \\ \frac{5}{1.326} & =\sigma \\ \sigma & =3.7707 \end{aligned} \end{aligned} $$
$$ \begin{aligned} &\text { Dari (1), }\\ &\begin{aligned} 25-\mu & =-0.151 \sigma \\ 25-\mu & =-0.151(3.7707) \\ -\mu & =-0.5694-25 \\ -\mu & =-25.5694 \\ \mu & =25.5694 \end{aligned} \end{aligned} $$

$$ \begin{aligned} P(X<18.5) & =\frac{1}{n} \\ P\left(Z<\frac{18.5-25.57}{3.77}\right) & =\frac{1}{n} \\ P(Z<-1.875) & =\frac{1}{n} \\ 0.0303 & =\frac{1}{n} \\ n & =\frac{1}{0.0303} \\ n & =33 \end{aligned} $$