Soalan 3:
(a)
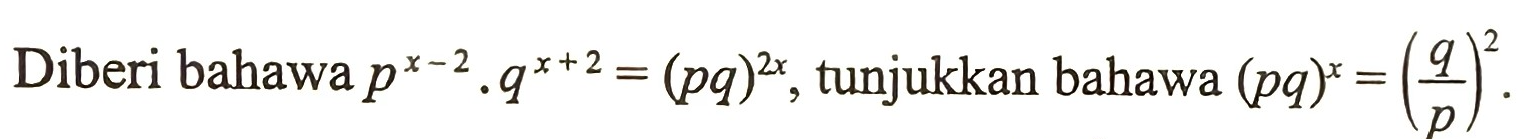
[3 markah]
(b)

Jawapan:
(a)
$$ \begin{aligned} p^{x-2} \cdot q^{x+2} & =(p q)^{2 x} \\ \left(\frac{p^x}{p^2}\right)\left(q^x\right)\left(q^2\right) & =(p q)^{2 x} \\ (p q)^x\left(\frac{q^2}{p^2}\right) & =(p q)^{2 x} \\ \left(\frac{q}{p}\right)^2 & =\frac{(p q)^{2 x}}{(p q)^x} \\ \left(\frac{q}{p}\right)^2 & =(p q)^{2 x-x} \\ \left(\frac{q}{p}\right)^2 & =(p q)^x(\text { Ditunjukkan }) \end{aligned} $$
(b)
$$ \begin{aligned} \frac{k}{4-\sqrt{7}}+\sqrt{28} & =\frac{k}{4-\sqrt{7}}+\sqrt{28}\left(\frac{4-\sqrt{7}}{4-\sqrt{7}}\right) \\ & =\frac{k+\sqrt{28}(4-\sqrt{7})}{4-\sqrt{7}} \\ & =\frac{k+4 \sqrt{28}-\sqrt{196}}{4-\sqrt{7}} \\ & =\frac{k+4(2 \sqrt{7})-14}{4-\sqrt{7}} \\ & =\frac{k-14+8 \sqrt{7}}{4-\sqrt{7}} \times \frac{4+\sqrt{7}}{4+\sqrt{7}} \\ & =\frac{4 k-56+32 \sqrt{7}+k \sqrt{7}-14 \sqrt{7}+56}{16-7} \\ & =\frac{4 k+(18+k) \sqrt{7}}{9} \\ & =\frac{4 k}{9}+\left(\frac{18+k}{9}\right) \sqrt{7} \\ p=\frac{4 k}{9}, q= & \frac{18+k}{9} \end{aligned} $$
(a)
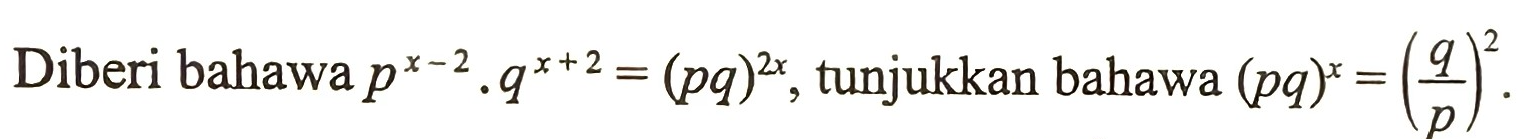
[3 markah]
(b)

Jawapan:
(a)
$$ \begin{aligned} p^{x-2} \cdot q^{x+2} & =(p q)^{2 x} \\ \left(\frac{p^x}{p^2}\right)\left(q^x\right)\left(q^2\right) & =(p q)^{2 x} \\ (p q)^x\left(\frac{q^2}{p^2}\right) & =(p q)^{2 x} \\ \left(\frac{q}{p}\right)^2 & =\frac{(p q)^{2 x}}{(p q)^x} \\ \left(\frac{q}{p}\right)^2 & =(p q)^{2 x-x} \\ \left(\frac{q}{p}\right)^2 & =(p q)^x(\text { Ditunjukkan }) \end{aligned} $$
(b)
$$ \begin{aligned} \frac{k}{4-\sqrt{7}}+\sqrt{28} & =\frac{k}{4-\sqrt{7}}+\sqrt{28}\left(\frac{4-\sqrt{7}}{4-\sqrt{7}}\right) \\ & =\frac{k+\sqrt{28}(4-\sqrt{7})}{4-\sqrt{7}} \\ & =\frac{k+4 \sqrt{28}-\sqrt{196}}{4-\sqrt{7}} \\ & =\frac{k+4(2 \sqrt{7})-14}{4-\sqrt{7}} \\ & =\frac{k-14+8 \sqrt{7}}{4-\sqrt{7}} \times \frac{4+\sqrt{7}}{4+\sqrt{7}} \\ & =\frac{4 k-56+32 \sqrt{7}+k \sqrt{7}-14 \sqrt{7}+56}{16-7} \\ & =\frac{4 k+(18+k) \sqrt{7}}{9} \\ & =\frac{4 k}{9}+\left(\frac{18+k}{9}\right) \sqrt{7} \\ p=\frac{4 k}{9}, q= & \frac{18+k}{9} \end{aligned} $$
Soalan 4:
Rajah 2 menunjukkan segi tiga ABC. AR adalah selari dengan PQ.
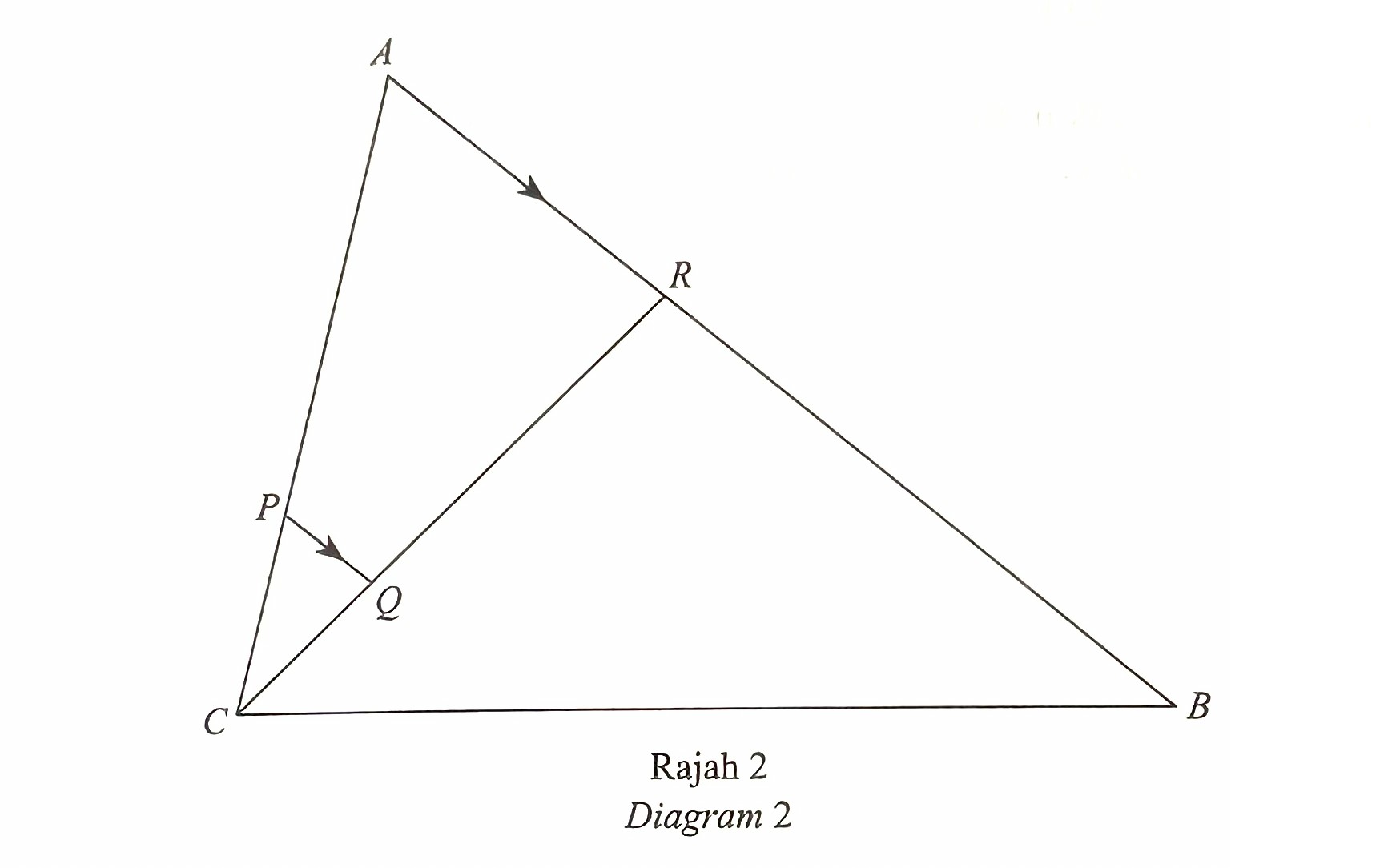
$$ \text { Diberi bahawa } \overrightarrow{C B}=6 \underline{u}, \overrightarrow{C A}=5 \underline{v} \text { dan } \overrightarrow{A R}=\frac{2}{5} \overrightarrow{A B} \text {. } $$
$$ \text { (a) Ungkapkan dalam sebutan } \underline{u} \text { dan } \underline{v} \text { : } $$
$$ \text { (i) } \overrightarrow{A B} \text {, } $$
$$ \text { (ii) } \overrightarrow{C R} \text {. } $$
[3 markah]
(b)(i)
$$ \text { Diberi bahawa } \underline{u}=5 \underline{i} \text { dan } \underline{v}=\underline{i}+4 \underline{j} \text {, cari }|\overrightarrow{C R}| \text {. } $$
(b)(ii)
Seterusnya, cari jarak terdekat dari titik A ke garis lurus CR jika luas Δ CPQ ialah 40/3 unit2 dan CQ : QR = 1 : 2.
[5 markah]
Jawapan:
(a)(i)
$$ \begin{aligned} \overrightarrow{A B} & =\overrightarrow{A C}+\overrightarrow{C B} \\ & =-5 \underline{v}+6 \underline{u} \end{aligned} $$
(a)(ii)
$$ \begin{aligned} \overrightarrow{C R} & =\overrightarrow{C A}+\overrightarrow{A R} \\ & =5 \underline{v}+\frac{2}{5} \overrightarrow{A B} \\ & =5 \underline{v}+\frac{2}{5}(-5 \underline{v}+6 \underline{u}) \\ & =5 \underline{v}-2 \underline{v}+\frac{12}{5} \underline{u} \\ & =3 \underline{v}+\frac{12}{5} \underline{u} \end{aligned} $$
(b)(i)
$$ \begin{aligned} & \overrightarrow{C R}=3(\underline{i}+4 \underline{j})+\frac{12}{5}(5 \underline{i}) \\ & \overrightarrow{C R}=3 \underline{i}+12 \underline{j}+12 \underline{i} \\ & \overrightarrow{C R}=15 \underline{i}+12 \underline{j} \\ & |\overrightarrow{C R}|=\sqrt{15^2+12^2} \\ & |\overrightarrow{C R}|=3 \sqrt{41} \end{aligned} $$
(b)(ii)
$$ \begin{aligned} &\begin{aligned} \text { Luas, } \triangle C A R & =3 \times \triangle C P Q \\ \frac{1}{2} \times C R \times \text { tinggi } & =3\left(\frac{40}{3}\right) \\ \frac{1}{2} \times 3 \sqrt{41} \times x & =40 \\ 3 \sqrt{41} \times x & =80 \\ x & =\frac{80}{3 \sqrt{41}} \\ x & =\frac{80}{3 \sqrt{41}} \times \frac{3 \sqrt{41}}{3 \sqrt{41}} \\ x & =\frac{80 \sqrt{41}}{123} \end{aligned}\\ &\therefore \text { Jarak terdekat } =4.1646 \text { unit } \end{aligned} $$
Rajah 2 menunjukkan segi tiga ABC. AR adalah selari dengan PQ.

$$ \text { Diberi bahawa } \overrightarrow{C B}=6 \underline{u}, \overrightarrow{C A}=5 \underline{v} \text { dan } \overrightarrow{A R}=\frac{2}{5} \overrightarrow{A B} \text {. } $$
$$ \text { (a) Ungkapkan dalam sebutan } \underline{u} \text { dan } \underline{v} \text { : } $$
$$ \text { (i) } \overrightarrow{A B} \text {, } $$
$$ \text { (ii) } \overrightarrow{C R} \text {. } $$
[3 markah]
(b)(i)
$$ \text { Diberi bahawa } \underline{u}=5 \underline{i} \text { dan } \underline{v}=\underline{i}+4 \underline{j} \text {, cari }|\overrightarrow{C R}| \text {. } $$
(b)(ii)
Seterusnya, cari jarak terdekat dari titik A ke garis lurus CR jika luas Δ CPQ ialah 40/3 unit2 dan CQ : QR = 1 : 2.
[5 markah]
Jawapan:
(a)(i)
$$ \begin{aligned} \overrightarrow{A B} & =\overrightarrow{A C}+\overrightarrow{C B} \\ & =-5 \underline{v}+6 \underline{u} \end{aligned} $$
(a)(ii)
$$ \begin{aligned} \overrightarrow{C R} & =\overrightarrow{C A}+\overrightarrow{A R} \\ & =5 \underline{v}+\frac{2}{5} \overrightarrow{A B} \\ & =5 \underline{v}+\frac{2}{5}(-5 \underline{v}+6 \underline{u}) \\ & =5 \underline{v}-2 \underline{v}+\frac{12}{5} \underline{u} \\ & =3 \underline{v}+\frac{12}{5} \underline{u} \end{aligned} $$
(b)(i)
$$ \begin{aligned} & \overrightarrow{C R}=3(\underline{i}+4 \underline{j})+\frac{12}{5}(5 \underline{i}) \\ & \overrightarrow{C R}=3 \underline{i}+12 \underline{j}+12 \underline{i} \\ & \overrightarrow{C R}=15 \underline{i}+12 \underline{j} \\ & |\overrightarrow{C R}|=\sqrt{15^2+12^2} \\ & |\overrightarrow{C R}|=3 \sqrt{41} \end{aligned} $$
(b)(ii)
$$ \begin{aligned} &\begin{aligned} \text { Luas, } \triangle C A R & =3 \times \triangle C P Q \\ \frac{1}{2} \times C R \times \text { tinggi } & =3\left(\frac{40}{3}\right) \\ \frac{1}{2} \times 3 \sqrt{41} \times x & =40 \\ 3 \sqrt{41} \times x & =80 \\ x & =\frac{80}{3 \sqrt{41}} \\ x & =\frac{80}{3 \sqrt{41}} \times \frac{3 \sqrt{41}}{3 \sqrt{41}} \\ x & =\frac{80 \sqrt{41}}{123} \end{aligned}\\ &\therefore \text { Jarak terdekat } =4.1646 \text { unit } \end{aligned} $$