Soalan 1:
Rajah 1 menunjukkan sektor BAC dengan pusat A dan sektor COD dengan pusat O. P berada pada garis lurus OD.
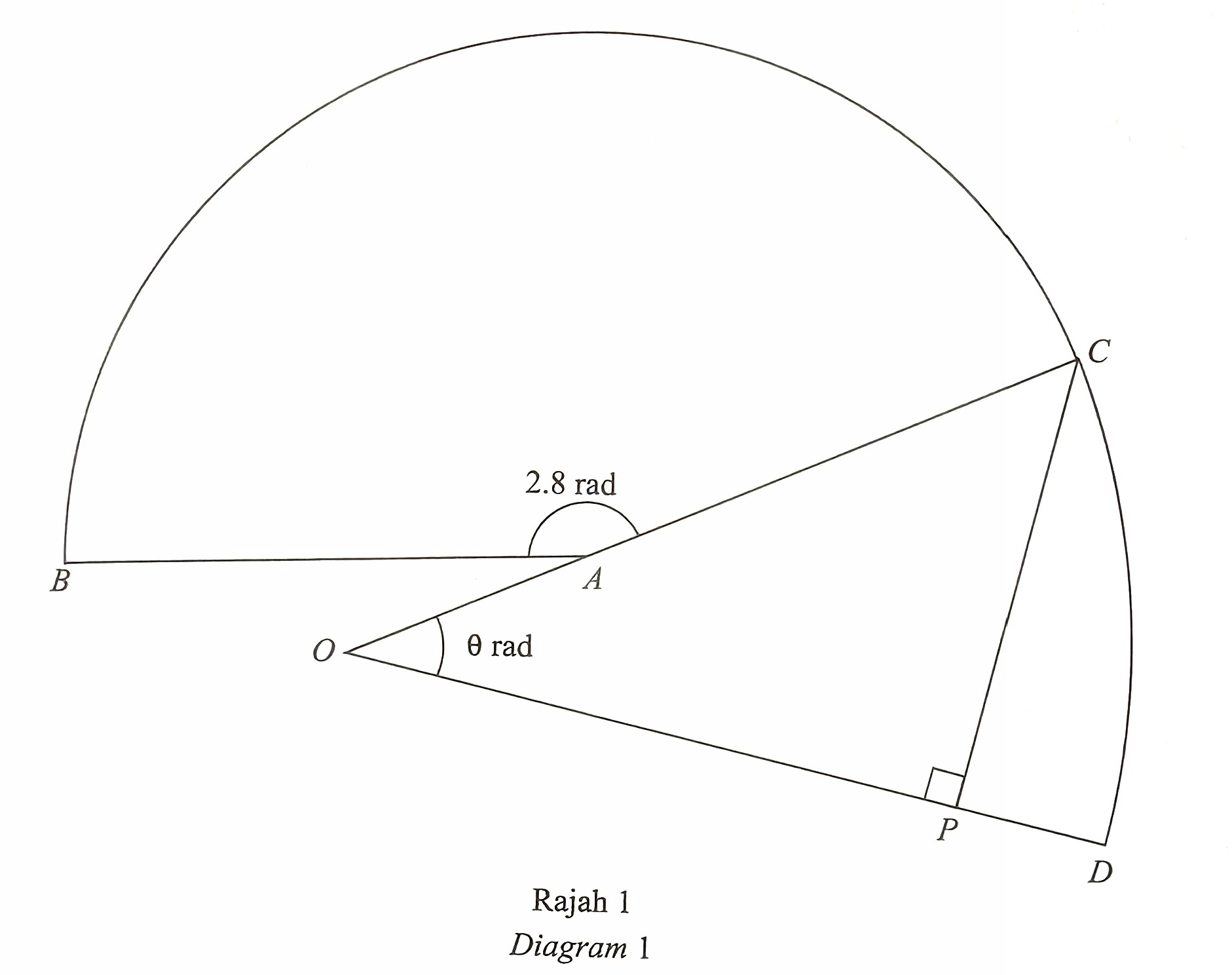
Diberi bahawa luas sektor BAC ialah 113.4 cm2, OA = ½ AC dan CP = 7.74 cm.
[Guna π = 3.142]
(a)(i) Cari panjang AC, dalam cm .
(ii) Tunjukkan bahawa θ = 0.611 apabila dibundarkan kepada tiga angka bererti.
[4 markah]
(b) Seterusnya, cari perimeter, dalam cm, bagi seluruh rajah.
[3 markah]
Jawapan:
(a)(i)
$$ \begin{aligned} \text { Luas } & = \frac{1}{2} j^2 \theta \\ \frac{1}{2}(A C)^2(2.8) & =113.4 \\ (A C)^2 & =\frac{113.4}{(2.8)\left(\frac{1}{2}\right)} \\ (A C)^2 & =81 \\ A C & =\sqrt{81} \\ A C & =9 \mathrm{~cm} \end{aligned} $$
(a)(ii)
$$ \begin{aligned} O A & =\frac{1}{2} A C=4.5 \mathrm{~cm} \\ \therefore O C & =4.5 \mathrm{~cm}+9 \mathrm{~cm} \\ & =13.5 \mathrm{~cm} \\ \sin \theta & =\frac{C P}{O C} \\ \sin \theta & =\frac{7.74}{13.5} \\ \theta & =\sin ^{-1}\left(\frac{7.74}{13.5}\right) \\ \theta & =34.98^{\circ} \\ \theta & =0.6106 \mathrm{rad} \\ \theta & =0.611 \mathrm{rad} \end{aligned} $$
(b)
$$ \begin{aligned} S_{C D} & =(13.5)(0.611) \\ & =8.2485 \mathrm{~cm} \\ S_{B C} & =(9)(2.8) \\ & =25.2 \mathrm{~cm} \\ \text { Perimeter } & =A B+B C+C D+D O+O A \\ & =9+25.2+8.2485+13.5+4.5 \\ & =60.4485 \mathrm{~cm} \end{aligned} $$
Rajah 1 menunjukkan sektor BAC dengan pusat A dan sektor COD dengan pusat O. P berada pada garis lurus OD.

Diberi bahawa luas sektor BAC ialah 113.4 cm2, OA = ½ AC dan CP = 7.74 cm.
[Guna π = 3.142]
(a)(i) Cari panjang AC, dalam cm .
(ii) Tunjukkan bahawa θ = 0.611 apabila dibundarkan kepada tiga angka bererti.
[4 markah]
(b) Seterusnya, cari perimeter, dalam cm, bagi seluruh rajah.
[3 markah]
Jawapan:
(a)(i)
$$ \begin{aligned} \text { Luas } & = \frac{1}{2} j^2 \theta \\ \frac{1}{2}(A C)^2(2.8) & =113.4 \\ (A C)^2 & =\frac{113.4}{(2.8)\left(\frac{1}{2}\right)} \\ (A C)^2 & =81 \\ A C & =\sqrt{81} \\ A C & =9 \mathrm{~cm} \end{aligned} $$
(a)(ii)
$$ \begin{aligned} O A & =\frac{1}{2} A C=4.5 \mathrm{~cm} \\ \therefore O C & =4.5 \mathrm{~cm}+9 \mathrm{~cm} \\ & =13.5 \mathrm{~cm} \\ \sin \theta & =\frac{C P}{O C} \\ \sin \theta & =\frac{7.74}{13.5} \\ \theta & =\sin ^{-1}\left(\frac{7.74}{13.5}\right) \\ \theta & =34.98^{\circ} \\ \theta & =0.6106 \mathrm{rad} \\ \theta & =0.611 \mathrm{rad} \end{aligned} $$
(b)
$$ \begin{aligned} S_{C D} & =(13.5)(0.611) \\ & =8.2485 \mathrm{~cm} \\ S_{B C} & =(9)(2.8) \\ & =25.2 \mathrm{~cm} \\ \text { Perimeter } & =A B+B C+C D+D O+O A \\ & =9+25.2+8.2485+13.5+4.5 \\ & =60.4485 \mathrm{~cm} \end{aligned} $$
Soalan 2:
Fungsi kuadratik f(x) = 3x2 + 3px + p, dengan keadaan p ialah pemalar, mempunyai nilai minimum -1 .
(a) Menggunakan kaedah penyempurnaan kuasa dua, cari nilai-nilai p. [4 markah]
(b) Lakar graf bagi f(x) menggunakan nilai p yang paling besar daripada (a). [2 markah]
Answer:
(a)
$$ \begin{aligned} & f(x)=3 x^2+3 p x+p \\ & f(x)=3\left(x^2+p x+\frac{p}{3}\right) \\ & f(x)=3\left[x^2+p x+\left(\frac{p}{2}\right)^2-\left(\frac{p}{2}\right)^2+\frac{p}{3}\right] \\ & f(x)=3\left[\left(x+\frac{p}{2}\right)^2-\frac{p^2}{4}+\frac{p}{3}\right] \\ & f(x)=3\left(x+\frac{p}{2}\right)^2-\frac{3 p^2}{4}+p \end{aligned} $$
$$ \begin{aligned} &\text { Nilai minimum }=-1\\ &\begin{aligned} -\frac{3 p^2}{4}+p & =-1 \\ -3 p^2+4 p & =-4 \\ -3 p^2+4 p+4 & =0 \\ 3 p^2-4 p-4 & =0 \\ (3 p+2)(p-2) & =0 \\ 3 p+2=0, p-2 & =0 \\ p=-\frac{2}{3}, p=2 & \end{aligned} \end{aligned} $$
(b)
$$ \begin{aligned} & p=2 ; f(x)=3\left(x+\frac{2}{2}\right)^2-\frac{3(2)^2}{4}+2 \\ & f(x)=3(x+1)^2-1 \end{aligned} $$
$$ \begin{aligned} &\text { Apabila } f(x)=0 \text {; }\\ &\begin{aligned} 3(x+1)^2-1 & =0 \\ (x+1)^2 & =\frac{1}{3} \\ x+1 & = \pm \sqrt{\frac{1}{3}} \\ x & =-1 \pm \sqrt{\frac{1}{3}} \end{aligned} \end{aligned} $$
$$ \begin{aligned} & \text { Apabila } x=0 \text {; } \\ & f(x)=3(0+1)^2-1 \\ & \begin{aligned} f(x)=2 & \\ \text { Apabila } x+1 & =0 \\ x & =-1 \end{aligned} \end{aligned} $$
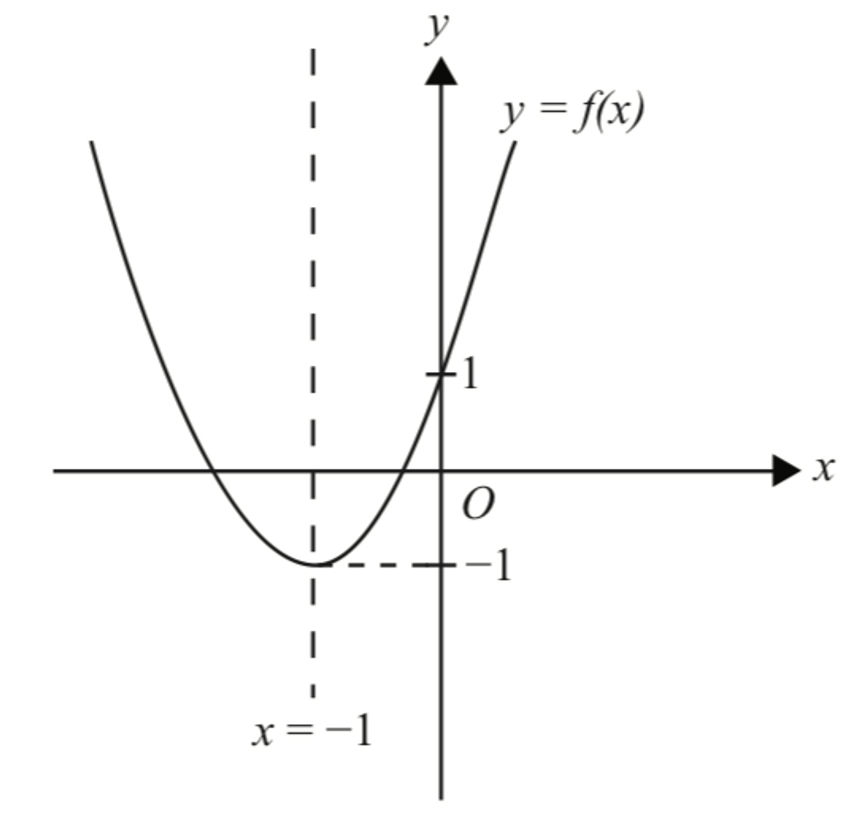
Fungsi kuadratik f(x) = 3x2 + 3px + p, dengan keadaan p ialah pemalar, mempunyai nilai minimum -1 .
(a) Menggunakan kaedah penyempurnaan kuasa dua, cari nilai-nilai p. [4 markah]
(b) Lakar graf bagi f(x) menggunakan nilai p yang paling besar daripada (a). [2 markah]
Answer:
(a)
$$ \begin{aligned} & f(x)=3 x^2+3 p x+p \\ & f(x)=3\left(x^2+p x+\frac{p}{3}\right) \\ & f(x)=3\left[x^2+p x+\left(\frac{p}{2}\right)^2-\left(\frac{p}{2}\right)^2+\frac{p}{3}\right] \\ & f(x)=3\left[\left(x+\frac{p}{2}\right)^2-\frac{p^2}{4}+\frac{p}{3}\right] \\ & f(x)=3\left(x+\frac{p}{2}\right)^2-\frac{3 p^2}{4}+p \end{aligned} $$
$$ \begin{aligned} &\text { Nilai minimum }=-1\\ &\begin{aligned} -\frac{3 p^2}{4}+p & =-1 \\ -3 p^2+4 p & =-4 \\ -3 p^2+4 p+4 & =0 \\ 3 p^2-4 p-4 & =0 \\ (3 p+2)(p-2) & =0 \\ 3 p+2=0, p-2 & =0 \\ p=-\frac{2}{3}, p=2 & \end{aligned} \end{aligned} $$
(b)
$$ \begin{aligned} & p=2 ; f(x)=3\left(x+\frac{2}{2}\right)^2-\frac{3(2)^2}{4}+2 \\ & f(x)=3(x+1)^2-1 \end{aligned} $$
$$ \begin{aligned} &\text { Apabila } f(x)=0 \text {; }\\ &\begin{aligned} 3(x+1)^2-1 & =0 \\ (x+1)^2 & =\frac{1}{3} \\ x+1 & = \pm \sqrt{\frac{1}{3}} \\ x & =-1 \pm \sqrt{\frac{1}{3}} \end{aligned} \end{aligned} $$
$$ \begin{aligned} & \text { Apabila } x=0 \text {; } \\ & f(x)=3(0+1)^2-1 \\ & \begin{aligned} f(x)=2 & \\ \text { Apabila } x+1 & =0 \\ x & =-1 \end{aligned} \end{aligned} $$
