Soalan 7:
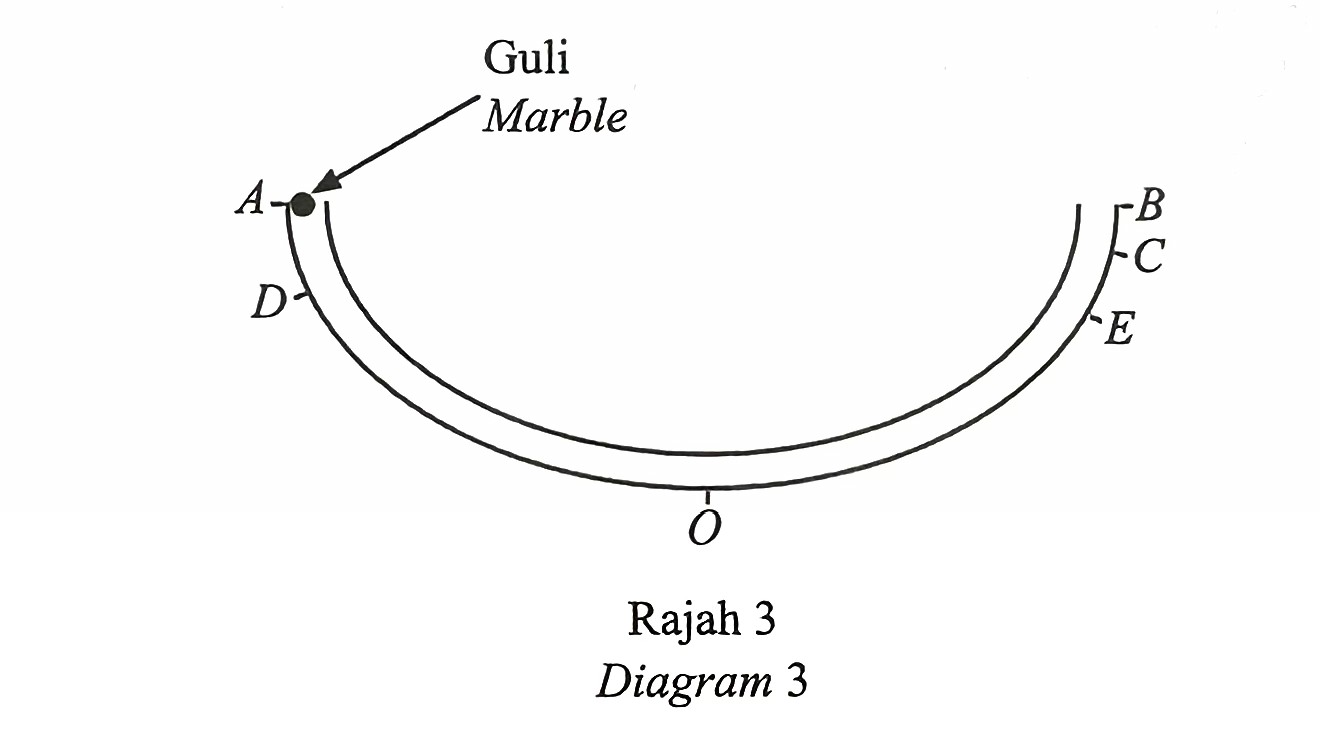
Rajah 3 menunjukkan sebuah tiub yang simetri dengan keadaan titik A dan titik B berada pada aras yang sama.
Sebiji guli dilepaskan dari titik A dan bergerak melalui tiub menuju ke arah titik B sehingga ia berhenti seketika buat kali pertama di titik C.
Guli itu akan bergerak secara ulang alik melalui tiub sehingga ia berhenti sepenuhnya di titik O.
Guli itu berhenti seketika buat kali kedua di titik D dan berhenti seketika buat kali ketiga di titik E.
Jarak yang dilalui oleh guli itu dari titik A ke titik C, titik C ke titik D dan jarak seterusnya adalah dalam nisbah yang sama.
Jumlah jarak yang dilalui oleh guli tersebut dari titik A ke titik C dan kemudian dari titik C ke titik D ialah 629/4 cm. Jarak yang dilalui dari titik D ke titik E ialah 4913/80 cm.
Jika guli itu mengambil masa selama 1 minit untuk berhenti sepenuhnya di titik O, tentukan sama ada laju purata guli itu adalah melebihi 10 cm s-1 atau tidak. Tunjukkan pengiraan anda.
[10 markah]
Jawapan:
Jarak yang dilalui dalam nisbah sama → Janjang geometri
$$ \begin{aligned} & T_1: A \rightarrow C \\ & T_2: C \rightarrow D \\ & T_3: D \rightarrow E \end{aligned} $$
$$ \begin{gathered} T_1+T_2=\frac{629}{4} \\ a+a r^{2-1}=\frac{629}{4} \\ a+a r=\frac{629}{4} \\ a(1+r)=\frac{629}{4} \ldots \text { (1) } \\ T_3=\frac{4913}{80} \\ a r^{3-1}=\frac{4913}{80} \\ a r^2=\frac{4913}{80} \ldots \text { (2) } \end{gathered} $$
$$ \frac{(2)}{(1)} ; \quad \frac{a r^2}{a(1+r)}=\frac{\left(\frac{4913}{80}\right)}{\left(\frac{629}{4}\right)} $$
$$ \begin{aligned} \frac{r^2}{1+r} & =\frac{289}{740} & \\ 740 r^2 & =289+289 r & \\ 740 r^2-289 r-289 & =0 & \\ (20 r-17)(37 r+17) & =0 & \\ 20 r-17=0 \quad, \quad 37 r+17 & =0 & \\ r=\frac{17}{20} \quad ; \quad r & =-\frac{17}{37}(\text { abai } ) & \end{aligned} $$
$$ \begin{aligned} &\text { Dari (1), }\\ &\begin{aligned} a(1+r) & =\frac{629}{4} \\ a\left(1+\frac{17}{20}\right) & =\frac{629}{4} \\ \frac{37}{20} a & =\frac{629}{4} \\ a & =\frac{\left(\frac{629}{4}\right)}{\left(\frac{37}{20}\right)} \\ a & =85 \end{aligned} \end{aligned} $$
$$ \begin{aligned} \text { Jumlah jarak } & =S_{\infty} \\ & =\frac{85}{1-\frac{17}{20}} \\ & =566 \frac{2}{3} \mathrm{~cm} \\ \text { Purata laju } & =\frac{566 \frac{2}{3} \mathrm{~cm}}{60 \mathrm{~s}} \\ & =9.44 \mathrm{~cm} \mathrm{~s}^{-1} \end{aligned} $$
$$ 9.44 \mathrm{~cm} \mathrm{~s}^{-1}<10 \mathrm{~cm} \mathrm{~s}^{-1} $$
Purata laju guli adalah tidak melebihi 10 cm s-1.
Rajah 3 menunjukkan sebuah tiub yang simetri dengan keadaan titik A dan titik B berada pada aras yang sama.
Sebiji guli dilepaskan dari titik A dan bergerak melalui tiub menuju ke arah titik B sehingga ia berhenti seketika buat kali pertama di titik C.
Guli itu akan bergerak secara ulang alik melalui tiub sehingga ia berhenti sepenuhnya di titik O.
Guli itu berhenti seketika buat kali kedua di titik D dan berhenti seketika buat kali ketiga di titik E.
Jarak yang dilalui oleh guli itu dari titik A ke titik C, titik C ke titik D dan jarak seterusnya adalah dalam nisbah yang sama.

Jumlah jarak yang dilalui oleh guli tersebut dari titik A ke titik C dan kemudian dari titik C ke titik D ialah 629/4 cm. Jarak yang dilalui dari titik D ke titik E ialah 4913/80 cm.
Jika guli itu mengambil masa selama 1 minit untuk berhenti sepenuhnya di titik O, tentukan sama ada laju purata guli itu adalah melebihi 10 cm s-1 atau tidak. Tunjukkan pengiraan anda.
[10 markah]
Jawapan:
Jarak yang dilalui dalam nisbah sama → Janjang geometri
$$ \begin{aligned} & T_1: A \rightarrow C \\ & T_2: C \rightarrow D \\ & T_3: D \rightarrow E \end{aligned} $$
$$ \begin{gathered} T_1+T_2=\frac{629}{4} \\ a+a r^{2-1}=\frac{629}{4} \\ a+a r=\frac{629}{4} \\ a(1+r)=\frac{629}{4} \ldots \text { (1) } \\ T_3=\frac{4913}{80} \\ a r^{3-1}=\frac{4913}{80} \\ a r^2=\frac{4913}{80} \ldots \text { (2) } \end{gathered} $$
$$ \frac{(2)}{(1)} ; \quad \frac{a r^2}{a(1+r)}=\frac{\left(\frac{4913}{80}\right)}{\left(\frac{629}{4}\right)} $$
$$ \begin{aligned} \frac{r^2}{1+r} & =\frac{289}{740} & \\ 740 r^2 & =289+289 r & \\ 740 r^2-289 r-289 & =0 & \\ (20 r-17)(37 r+17) & =0 & \\ 20 r-17=0 \quad, \quad 37 r+17 & =0 & \\ r=\frac{17}{20} \quad ; \quad r & =-\frac{17}{37}(\text { abai } ) & \end{aligned} $$
$$ \begin{aligned} &\text { Dari (1), }\\ &\begin{aligned} a(1+r) & =\frac{629}{4} \\ a\left(1+\frac{17}{20}\right) & =\frac{629}{4} \\ \frac{37}{20} a & =\frac{629}{4} \\ a & =\frac{\left(\frac{629}{4}\right)}{\left(\frac{37}{20}\right)} \\ a & =85 \end{aligned} \end{aligned} $$
$$ \begin{aligned} \text { Jumlah jarak } & =S_{\infty} \\ & =\frac{85}{1-\frac{17}{20}} \\ & =566 \frac{2}{3} \mathrm{~cm} \\ \text { Purata laju } & =\frac{566 \frac{2}{3} \mathrm{~cm}}{60 \mathrm{~s}} \\ & =9.44 \mathrm{~cm} \mathrm{~s}^{-1} \end{aligned} $$
$$ 9.44 \mathrm{~cm} \mathrm{~s}^{-1}<10 \mathrm{~cm} \mathrm{~s}^{-1} $$
Purata laju guli adalah tidak melebihi 10 cm s-1.
Soalan 8:
(a)(i)
$$ \text { Buktikan bahawa kos } 2 \theta=\operatorname{kos}^2 \theta-\sin ^2 \theta \text {. } $$
(a)(ii)
$$ \text { Seterusnya, selesaikan persamaan } 3 \operatorname{kos}^2 \theta=2+3 \sin ^2 \theta \text { untuk } 180^{\circ} \leqslant \theta \leqslant 360^{\circ} \text {. } $$
[5 markah]
(b)(i)
$$ \text { Lakar graf } y=-\left|\operatorname{kos}^2 \theta-\sin ^2 \theta\right|+\frac{4}{5} \text { untuk } 0 \leqslant \theta \leqslant 2 \pi \text {. } $$
(b)(ii)
Terdapat 8 penyelesaian apabila y = h, dengan keadaan h ialah pemalar. Nyatakan julat nilai bagi h.
[5 markah]
Jawapan:
(a)(i)
$$ \begin{aligned} & \mathrm{kos} \ 2 \theta=\mathrm{kos} (\theta+\theta) \\ & \mathrm{kos} \ 2 \theta=\mathrm{kos} \ \theta \mathrm{kos} \ \theta-\sin \theta \sin \theta \\ & \mathrm{kos} \ 2 \theta=\mathrm{kos}^2 \theta-\sin ^2 \theta(\text { Terbukti }) \ \end{aligned} $$
(a)(ii)
$$ \begin{aligned} &\begin{aligned} 3 \mathrm{kos}^2 \theta & =2+3 \sin ^2 \theta \\ 3 \mathrm{kos}^2 \theta-3 \sin ^2 \theta & =2 \\ 3\left(\mathrm{kos}^2 \theta-\sin ^2 \theta\right) & =2 \\ 3 \mathrm{kos} \ 2 \theta & =2 \\ \mathrm{kos} \ 2 \theta & =\frac{2}{3}(\mathrm{I}, \mathrm{IV}) \end{aligned}\\ &\text { Sudut rujukan : }\\ &\mathrm{kos}^{-1 /} \left(\frac{2}{3}\right)=48.19^{\circ} \quad ; \quad \begin{aligned} & 180^{\circ} \leqslant \theta \leqslant 360^{\circ} \\ & 360^{\circ} \leqslant 2 \theta \leqslant 720^{\circ} \end{aligned} \end{aligned} $$
$$ \begin{aligned} 2 \theta & =48.19^{\circ}, 360^{\circ}-48.19^{\circ}, 360^{\circ}+48.19^{\circ}, 360^{\circ}+311.81^{\circ} \\ & =48.19^{\circ}, 311.81^{\circ}, 408.19^{\circ}, 671.81^{\circ} \\ \theta & =24.10^{\circ}, 155.91^{\circ}, 204.10^{\circ}, 335.91^{\circ} \\ \therefore \theta & =204.10^{\circ}, 335.91^{\circ} \end{aligned} $$
(b)(i)
$$ \begin{aligned} & y=-\left|\mathrm{kos}^2 \theta-\sin ^2 \theta\right|+\frac{4}{5} \\ & y=-|\mathrm{kos} \ 2 \theta|+\frac{4}{5}, 0 \leqslant \theta \leqslant 2 \pi \end{aligned} $$
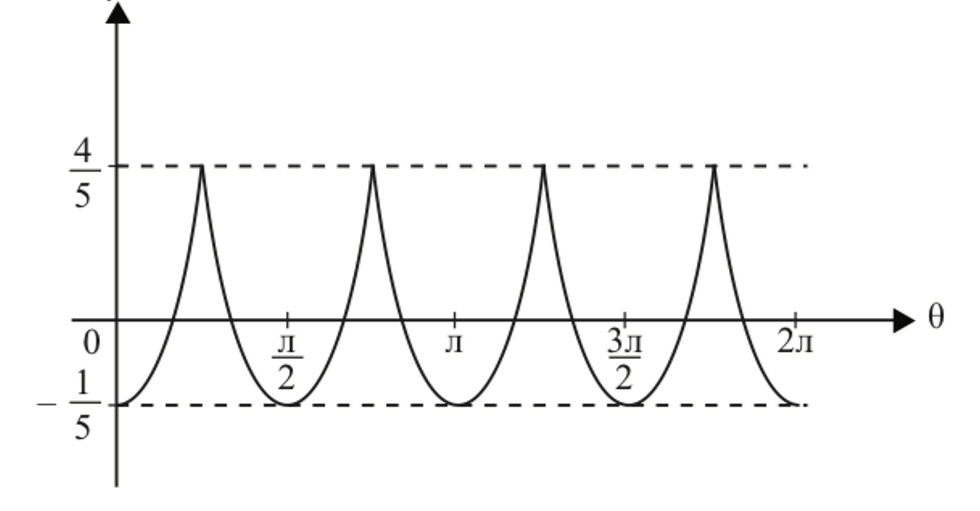
(b)(ii)
$$ -\frac{1}{5}<h<\frac{4}{5} $$
(a)(i)
$$ \text { Buktikan bahawa kos } 2 \theta=\operatorname{kos}^2 \theta-\sin ^2 \theta \text {. } $$
(a)(ii)
$$ \text { Seterusnya, selesaikan persamaan } 3 \operatorname{kos}^2 \theta=2+3 \sin ^2 \theta \text { untuk } 180^{\circ} \leqslant \theta \leqslant 360^{\circ} \text {. } $$
[5 markah]
(b)(i)
$$ \text { Lakar graf } y=-\left|\operatorname{kos}^2 \theta-\sin ^2 \theta\right|+\frac{4}{5} \text { untuk } 0 \leqslant \theta \leqslant 2 \pi \text {. } $$
(b)(ii)
Terdapat 8 penyelesaian apabila y = h, dengan keadaan h ialah pemalar. Nyatakan julat nilai bagi h.
[5 markah]
Jawapan:
(a)(i)
$$ \begin{aligned} & \mathrm{kos} \ 2 \theta=\mathrm{kos} (\theta+\theta) \\ & \mathrm{kos} \ 2 \theta=\mathrm{kos} \ \theta \mathrm{kos} \ \theta-\sin \theta \sin \theta \\ & \mathrm{kos} \ 2 \theta=\mathrm{kos}^2 \theta-\sin ^2 \theta(\text { Terbukti }) \ \end{aligned} $$
(a)(ii)
$$ \begin{aligned} &\begin{aligned} 3 \mathrm{kos}^2 \theta & =2+3 \sin ^2 \theta \\ 3 \mathrm{kos}^2 \theta-3 \sin ^2 \theta & =2 \\ 3\left(\mathrm{kos}^2 \theta-\sin ^2 \theta\right) & =2 \\ 3 \mathrm{kos} \ 2 \theta & =2 \\ \mathrm{kos} \ 2 \theta & =\frac{2}{3}(\mathrm{I}, \mathrm{IV}) \end{aligned}\\ &\text { Sudut rujukan : }\\ &\mathrm{kos}^{-1 /} \left(\frac{2}{3}\right)=48.19^{\circ} \quad ; \quad \begin{aligned} & 180^{\circ} \leqslant \theta \leqslant 360^{\circ} \\ & 360^{\circ} \leqslant 2 \theta \leqslant 720^{\circ} \end{aligned} \end{aligned} $$
$$ \begin{aligned} 2 \theta & =48.19^{\circ}, 360^{\circ}-48.19^{\circ}, 360^{\circ}+48.19^{\circ}, 360^{\circ}+311.81^{\circ} \\ & =48.19^{\circ}, 311.81^{\circ}, 408.19^{\circ}, 671.81^{\circ} \\ \theta & =24.10^{\circ}, 155.91^{\circ}, 204.10^{\circ}, 335.91^{\circ} \\ \therefore \theta & =204.10^{\circ}, 335.91^{\circ} \end{aligned} $$
(b)(i)
$$ \begin{aligned} & y=-\left|\mathrm{kos}^2 \theta-\sin ^2 \theta\right|+\frac{4}{5} \\ & y=-|\mathrm{kos} \ 2 \theta|+\frac{4}{5}, 0 \leqslant \theta \leqslant 2 \pi \end{aligned} $$

(b)(ii)
$$ -\frac{1}{5}<h<\frac{4}{5} $$