Soalan 8:
Menyenaraikan semua sebutan bagi jujukan adalah tidak diterima.
Bongkah kayu berbentuk silinder dipotong kepada bahagian-bahagian untuk dijadikan perhiasan. Rajah 7 menunjukkan tiga bahagian pertama yang telah dipotong dan bahagian yang tinggal.
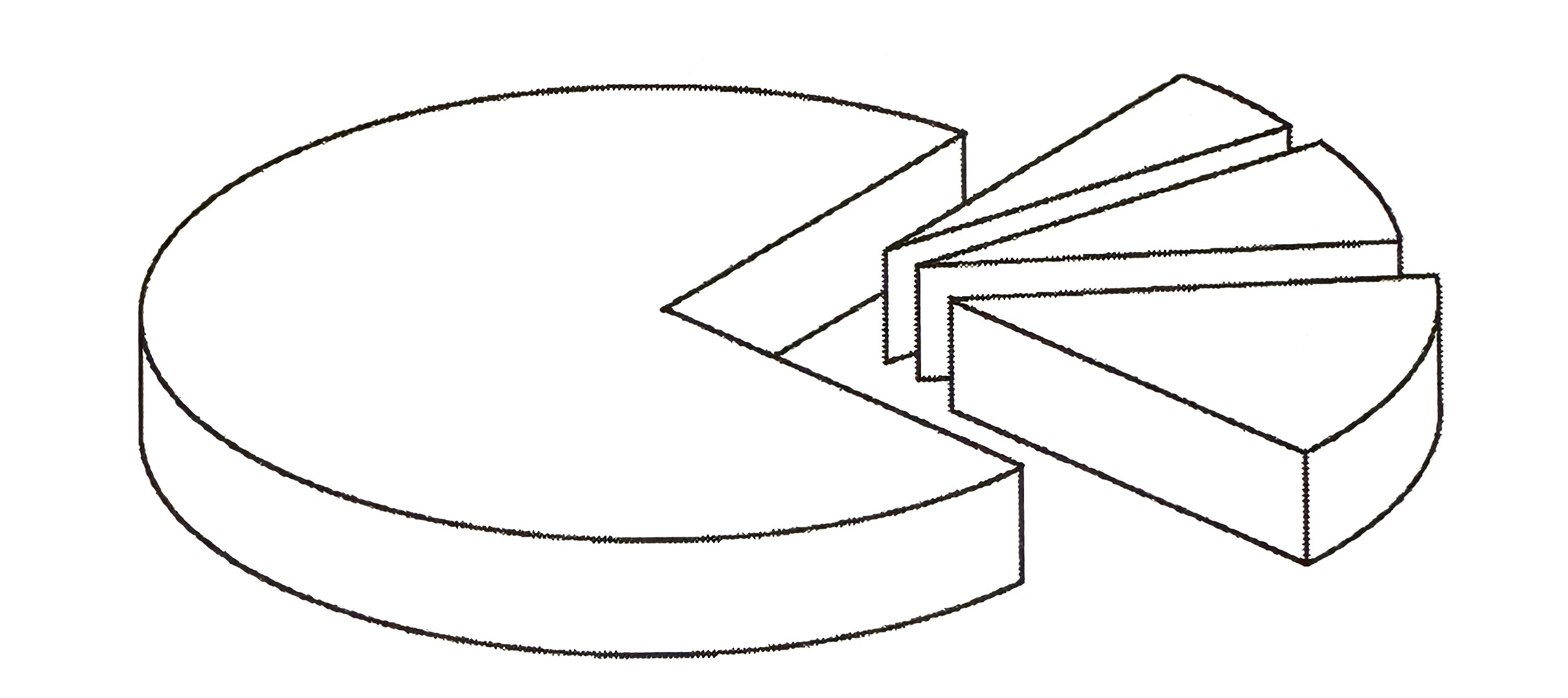
Sudut sektor meningkat dengan nilai malar untuk setiap bahagian berikutnya. Sejumlah n bahagian boleh dipotong daripada bongkah itu. Sudut sektor bahagian ke-4 adalah 3 kali sudut sektor bahagian terkecil. Jumlah sudut sektor bagi 4 bahagian pertama ialah 72∘.
(a) sudut sektor, dalam darjah, bahagian terkecil, [4 markah]
(b) nilai n. [3 markah]
Penyelesaian:
(a)
$$ \begin{aligned} &\text { Janjang Aritmetik, }\\ &\begin{aligned} T_n & =a+(n-1) d \\ S_n & =\frac{n}{2}[2 a+(n-1) d] \end{aligned} \end{aligned} $$
$$ \begin{aligned} T_4 & =3 T_1 \\ a+(4-1)(d) & =3 a \\ a+3 d & =3 a \\ 3 d & =2 a \ldots(1) \end{aligned} $$
$$ \begin{aligned} S_4 & =72^{\circ} \\ \frac{4}{2}[2 a+(4-1)(d)] & =72^{\circ} \\ 2(2 a+3 d) & =72^{\circ} \\ 2(2 a+2 a) & =72^{\circ} \\ 8 a & =72^{\circ} \\ a & =9^{\circ} \\ \text { Bahagian terkecil }=T_1 & =a=9^{\circ} \end{aligned} $$
(b)
$$ \text { Dari (1), } \begin{aligned} 3 d & =2(9) \\ 3 d & =18 \\ d & =6 \end{aligned} $$
$$ \begin{aligned} & S_n=360^{\circ} \\ & \frac{n}{2}[2(9)+(n-1)(6)]=360^{\circ} \\ & \frac{n}{2}(18+6 n-6)=360^{\circ} \\ & n(6 n+12)=720^{\circ} \\ & 6 n^2+12 n-720^{\circ}=0 \\ & n^2+2 n-120^{\circ}=0 \\ &(n-10)(n+12)=0 \\ & n-10=0, n+12=0 \\ & n=10, n=-12 \text { (abaikan) } \\ & \therefore n=10 \end{aligned} $$
Menyenaraikan semua sebutan bagi jujukan adalah tidak diterima.
Bongkah kayu berbentuk silinder dipotong kepada bahagian-bahagian untuk dijadikan perhiasan. Rajah 7 menunjukkan tiga bahagian pertama yang telah dipotong dan bahagian yang tinggal.

Sudut sektor meningkat dengan nilai malar untuk setiap bahagian berikutnya. Sejumlah n bahagian boleh dipotong daripada bongkah itu. Sudut sektor bahagian ke-4 adalah 3 kali sudut sektor bahagian terkecil. Jumlah sudut sektor bagi 4 bahagian pertama ialah 72∘.
(a) sudut sektor, dalam darjah, bahagian terkecil, [4 markah]
(b) nilai n. [3 markah]
Penyelesaian:
(a)
$$ \begin{aligned} &\text { Janjang Aritmetik, }\\ &\begin{aligned} T_n & =a+(n-1) d \\ S_n & =\frac{n}{2}[2 a+(n-1) d] \end{aligned} \end{aligned} $$
$$ \begin{aligned} T_4 & =3 T_1 \\ a+(4-1)(d) & =3 a \\ a+3 d & =3 a \\ 3 d & =2 a \ldots(1) \end{aligned} $$
$$ \begin{aligned} S_4 & =72^{\circ} \\ \frac{4}{2}[2 a+(4-1)(d)] & =72^{\circ} \\ 2(2 a+3 d) & =72^{\circ} \\ 2(2 a+2 a) & =72^{\circ} \\ 8 a & =72^{\circ} \\ a & =9^{\circ} \\ \text { Bahagian terkecil }=T_1 & =a=9^{\circ} \end{aligned} $$
(b)
$$ \text { Dari (1), } \begin{aligned} 3 d & =2(9) \\ 3 d & =18 \\ d & =6 \end{aligned} $$
$$ \begin{aligned} & S_n=360^{\circ} \\ & \frac{n}{2}[2(9)+(n-1)(6)]=360^{\circ} \\ & \frac{n}{2}(18+6 n-6)=360^{\circ} \\ & n(6 n+12)=720^{\circ} \\ & 6 n^2+12 n-720^{\circ}=0 \\ & n^2+2 n-120^{\circ}=0 \\ &(n-10)(n+12)=0 \\ & n-10=0, n+12=0 \\ & n=10, n=-12 \text { (abaikan) } \\ & \therefore n=10 \end{aligned} $$