Soalan 7:
(a) Rajah menunjukkan satu lengkung dan tangen kepada lengkung itu.
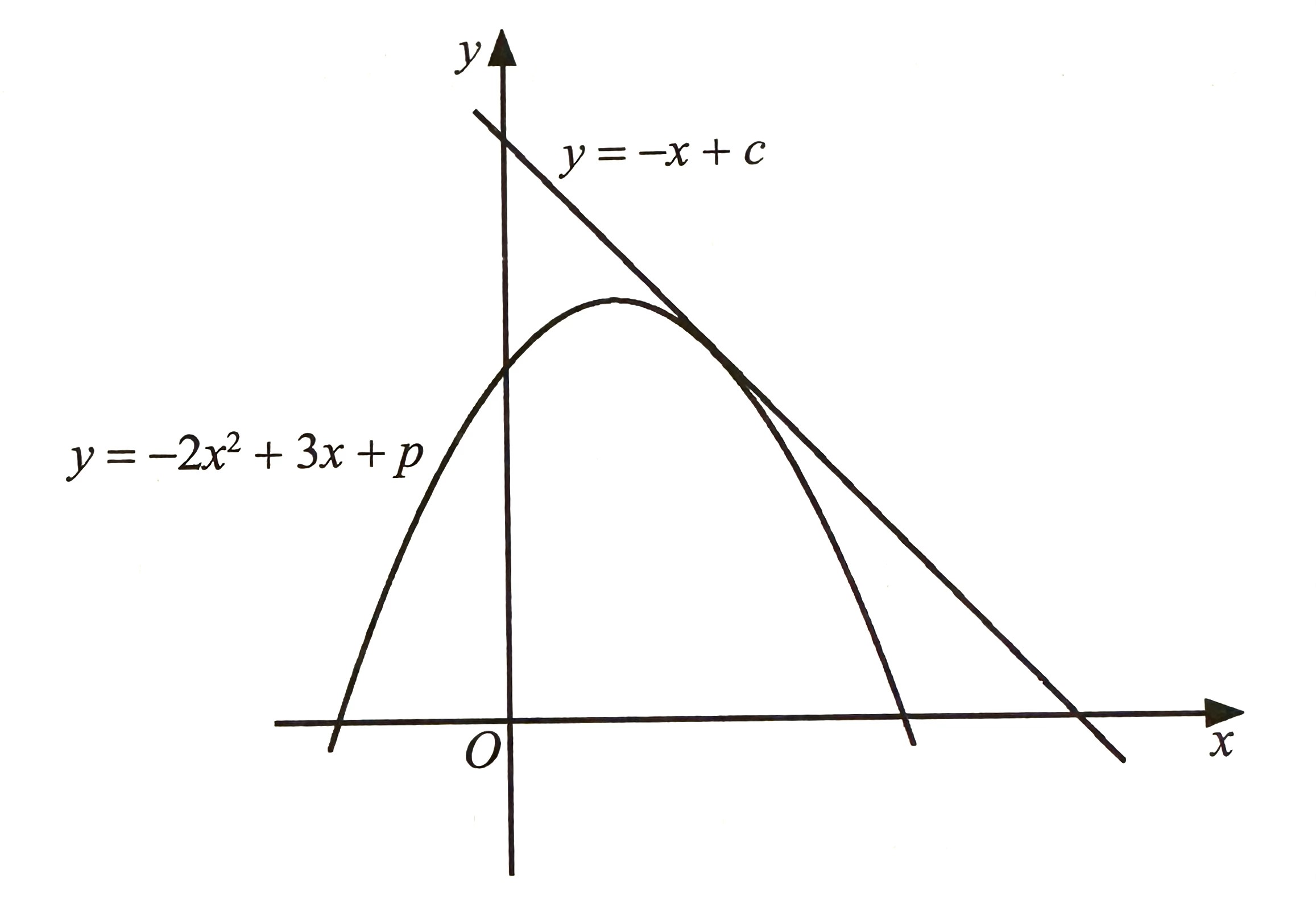Ungkapkan p dalam sebutan c.
[3 markah]
(b) Cari julat nilai x bagi (x + 1)(-3x – 3) < (x – 1) dengan menggunakan kaedah jadual.
[2 markah]
(c) Diberi bahawa p dan 2p ialah punca-punca bagi persamaan kuadratik 2x2 + 6x + 4p2 = 0.
Cari persamaan kuadratik yang mempunyai punca (p – 1) dan (p + 1).
[3 markah]
Penyelesaian:
(a)
$$ \begin{aligned} &\begin{aligned} & y=-x+c \ldots(1) \\ & y=-2 x^2+3 x+p \ldots(2) \end{aligned}\\ &\begin{aligned} (1)=(2):-2 x^2+3 x+p & =-x+c \\ -2 x^2+3 x+p+x-c & =0 \\ 2 x^2-4 x-p+c & =0 \\ a=2, \quad b=-4, \quad c & =-p+c \end{aligned} \end{aligned} $$
$$ \begin{aligned} &\text { Tangen kepada lengkung, }\\ &\begin{aligned} b^2-4 a c & =0 \\ (-4)^2-4(2)(-p+c) & =0 \\ 16-8(-p+c) & =0 \\ 16+8 p-8 c & =0 \\ 8 p & =8 c-16 \\ p & =c-2 \end{aligned} \end{aligned} $$
(b)
(x + 1)(-3x – 3) < x – 1
-3x2 – 3x – 3x – 3 – x + 1 < 0
-3x2 – 7x -2 < 0
3x2 – 7x – 2 > 0
(3x + 1)(x + 2) > 0
Apabila (3x + 1)(x + 2) = 0,
x = -1/3 atau -2
(c)
$$ \begin{aligned} & 2 x^2+6 x+4 p^2=0 \\ & \text { Punca-punca }=p, 2 p \\ & \text { HTP: } p+2 p=-\frac{6}{2} \\ & 3 p=-3 \\ & p=-1 \end{aligned} $$
$$ \begin{aligned} &\text { Punca baru: }\\ &\begin{aligned} p-1 & =-1-1, \\ & =-2 \\ p+1 & =-1+1 \\ & =0 \end{aligned} \end{aligned} $$
$$ \begin{aligned} & \text { HTP: }-2+0=-2 \\ & \text { HDP: }(-2)(0)=0 \end{aligned} $$
$$ \begin{aligned} & x^2-(\mathrm{HTP}) x+(\mathrm{HDP})=0 \\ & x^2-(-2) x+0=0 \\ & x^2+4 x=0 \end{aligned} $$
(a) Rajah menunjukkan satu lengkung dan tangen kepada lengkung itu.
Ungkapkan p dalam sebutan c. [3 markah]
(b) Cari julat nilai x bagi (x + 1)(-3x – 3) < (x – 1) dengan menggunakan kaedah jadual.
[2 markah]
(c) Diberi bahawa p dan 2p ialah punca-punca bagi persamaan kuadratik 2x2 + 6x + 4p2 = 0.
Cari persamaan kuadratik yang mempunyai punca (p – 1) dan (p + 1).
[3 markah]
Penyelesaian:
(a)
$$ \begin{aligned} &\begin{aligned} & y=-x+c \ldots(1) \\ & y=-2 x^2+3 x+p \ldots(2) \end{aligned}\\ &\begin{aligned} (1)=(2):-2 x^2+3 x+p & =-x+c \\ -2 x^2+3 x+p+x-c & =0 \\ 2 x^2-4 x-p+c & =0 \\ a=2, \quad b=-4, \quad c & =-p+c \end{aligned} \end{aligned} $$
$$ \begin{aligned} &\text { Tangen kepada lengkung, }\\ &\begin{aligned} b^2-4 a c & =0 \\ (-4)^2-4(2)(-p+c) & =0 \\ 16-8(-p+c) & =0 \\ 16+8 p-8 c & =0 \\ 8 p & =8 c-16 \\ p & =c-2 \end{aligned} \end{aligned} $$
(b)
(x + 1)(-3x – 3) < x – 1
-3x2 – 3x – 3x – 3 – x + 1 < 0
-3x2 – 7x -2 < 0
3x2 – 7x – 2 > 0
(3x + 1)(x + 2) > 0
Apabila (3x + 1)(x + 2) = 0,
x = -1/3 atau -2
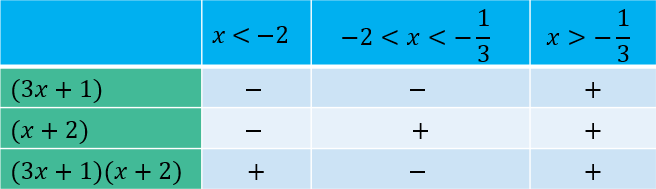
Daripada jadual,
(3x + 1)(x + 2) > 0 apabila x < -2 atau x > -1/3
∴ x < -2 atau x > -1/3
(c)
$$ \begin{aligned} & 2 x^2+6 x+4 p^2=0 \\ & \text { Punca-punca }=p, 2 p \\ & \text { HTP: } p+2 p=-\frac{6}{2} \\ & 3 p=-3 \\ & p=-1 \end{aligned} $$
$$ \begin{aligned} &\text { Punca baru: }\\ &\begin{aligned} p-1 & =-1-1, \\ & =-2 \\ p+1 & =-1+1 \\ & =0 \end{aligned} \end{aligned} $$
$$ \begin{aligned} & \text { HTP: }-2+0=-2 \\ & \text { HDP: }(-2)(0)=0 \end{aligned} $$
$$ \begin{aligned} & x^2-(\mathrm{HTP}) x+(\mathrm{HDP})=0 \\ & x^2-(-2) x+0=0 \\ & x^2+4 x=0 \end{aligned} $$