Soalan 1:
Diberi bahawa empat sebutan berturutan bagi suatu jujukan ialah 50, 45, x dan y. Nyatakan nilai bagi
(a) y – x jika jujukan itu ialah janjang aritmetik,
(b) y/x jika jujukan itu ialah janjang geometri.
[2 markah]
Penyelesaian:
(a)Diberi bahawa empat sebutan berturutan bagi suatu jujukan ialah 50, 45, x dan y. Nyatakan nilai bagi
(a) y – x jika jujukan itu ialah janjang aritmetik,
(b) y/x jika jujukan itu ialah janjang geometri.
[2 markah]
Penyelesaian:
$$ \begin{aligned} & y-x=45-50 \\ & y-x=-5 \end{aligned} $$
(b)
$$ \begin{aligned} & \frac{y}{x}=\frac{45}{50} \\ & \frac{y}{x}=\frac{9}{10} \end{aligned} $$
Soalan 2:
Rajah 1 menunjukkan dua garis lurus.
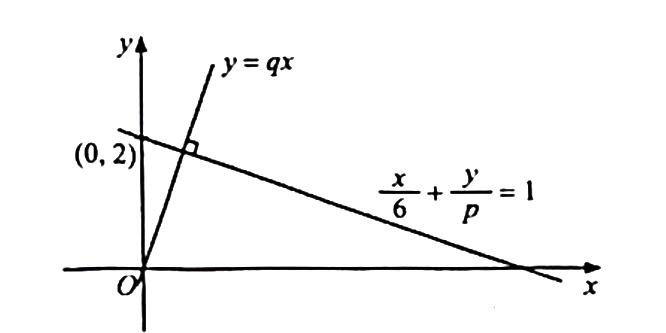
Cari nilai q?
[3 markah]
Penyelesaian:
$$ \begin{aligned} &p \text { ialah pintasan paksi- } y \\ &\begin{aligned} & \therefore p=2 \\ & \frac{x}{6}+\frac{y}{2}=1 \\ & \frac{y}{2}=-\frac{x}{6}+1 \\ & y=-\frac{1}{3} x+2 \\ & \therefore m_1=-\frac{1}{3} \\ & y=q x \\ & \therefore m_2=q \end{aligned} \end{aligned} $$
$$ \begin{aligned} &\frac{x}{6}+\frac{y}{2}=1 \text { berserenjang dengan } y=q x\\ &\begin{aligned} m_1 m_2 & =-1 \\ \left(-\frac{1}{3}\right) \times(q) & =-1 \\ q & =3 \end{aligned} \end{aligned} $$
Rajah 1 menunjukkan dua garis lurus.

Cari nilai q?
[3 markah]
Penyelesaian:
$$ \begin{aligned} &p \text { ialah pintasan paksi- } y \\ &\begin{aligned} & \therefore p=2 \\ & \frac{x}{6}+\frac{y}{2}=1 \\ & \frac{y}{2}=-\frac{x}{6}+1 \\ & y=-\frac{1}{3} x+2 \\ & \therefore m_1=-\frac{1}{3} \\ & y=q x \\ & \therefore m_2=q \end{aligned} \end{aligned} $$
$$ \begin{aligned} &\frac{x}{6}+\frac{y}{2}=1 \text { berserenjang dengan } y=q x\\ &\begin{aligned} m_1 m_2 & =-1 \\ \left(-\frac{1}{3}\right) \times(q) & =-1 \\ q & =3 \end{aligned} \end{aligned} $$
Soalan 3:
$$ \text { Rajah } 2 \text { menunjukkan dua garis lurus, } \mathrm{L}_1 \text { dan } \mathrm{L}_2 \text {, yang dilukis berdasarkan lima titik yang diplotkan pada satah } \frac{1}{y} \text { melawan } x^2 \text {. } $$
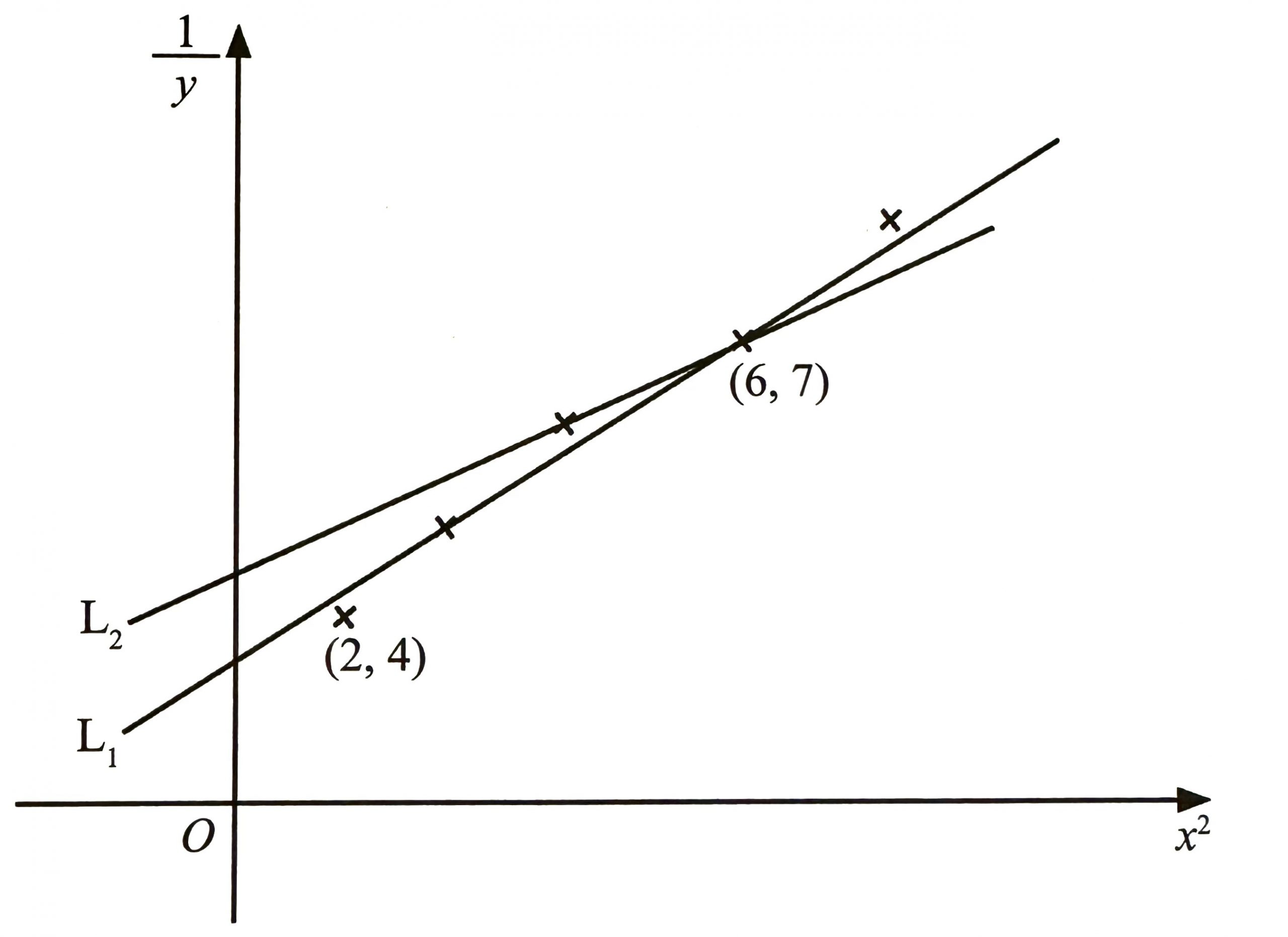
(a) Garis lurus manakah merupakan garis lurus penyuaian terbaik yang sesuai?
Beri sebab kepada jawapan anda.
[1 markah]
(b) Diberi bahawa (10, 9) terletak pada garis lurus penyuaian terbaik itu, ungkapkan y dalam sebutan x.
[3 markah]
Penyelesaian:
(a)
L1 lebih sesuai kerana garis lurus tersebut melalui sebanyak mungkin titik dan terdapat jumlah titik yang sama di kedua-dua belah garis lurus.
(b)
$$ \begin{aligned} Y & =m X+C \\ \frac{1}{y} & =\frac{(7-4)}{(6-2)}\left(x^2\right)+C \\ \frac{1}{y} & =\frac{3}{4} x^2+C \end{aligned} $$
$$ \begin{aligned} & \text Pada (10,9), \\ & 9=\frac{3}{4}(10)+C \\ & 9=\frac{15}{2}+C \\ & \frac{3}{2}=C \end{aligned} $$
$$ \begin{aligned} & \frac{1}{y}=\frac{3}{4} x^2+\frac{3}{2} \\ & \frac{1}{y}=\frac{3 x^2+6}{4} \\ & \frac{y}{1}=\frac{4}{3 x^2+6} \\ & y=\frac{3}{4 x^2+6} \end{aligned} $$
$$ \text { Rajah } 2 \text { menunjukkan dua garis lurus, } \mathrm{L}_1 \text { dan } \mathrm{L}_2 \text {, yang dilukis berdasarkan lima titik yang diplotkan pada satah } \frac{1}{y} \text { melawan } x^2 \text {. } $$

(a) Garis lurus manakah merupakan garis lurus penyuaian terbaik yang sesuai?
Beri sebab kepada jawapan anda.
[1 markah]
(b) Diberi bahawa (10, 9) terletak pada garis lurus penyuaian terbaik itu, ungkapkan y dalam sebutan x.
[3 markah]
Penyelesaian:
(a)
L1 lebih sesuai kerana garis lurus tersebut melalui sebanyak mungkin titik dan terdapat jumlah titik yang sama di kedua-dua belah garis lurus.
(b)
$$ \begin{aligned} Y & =m X+C \\ \frac{1}{y} & =\frac{(7-4)}{(6-2)}\left(x^2\right)+C \\ \frac{1}{y} & =\frac{3}{4} x^2+C \end{aligned} $$
$$ \begin{aligned} & \text Pada (10,9), \\ & 9=\frac{3}{4}(10)+C \\ & 9=\frac{15}{2}+C \\ & \frac{3}{2}=C \end{aligned} $$
$$ \begin{aligned} & \frac{1}{y}=\frac{3}{4} x^2+\frac{3}{2} \\ & \frac{1}{y}=\frac{3 x^2+6}{4} \\ & \frac{y}{1}=\frac{4}{3 x^2+6} \\ & y=\frac{3}{4 x^2+6} \end{aligned} $$