2.7.2 Pembezaan, SPM Praktis (Kertas 1 Soalan 11 - 20)

Soalan 11:

Diberi fungsi graf

f (x) = h x^{3} + \frac{k}{x^{2}}

mempunyai fungsi kecerunan

f ‘ (x) = 12 x^{2} - \frac{258}{x^{3}}

dengan h dan k ialah pemalar. Cari nilai h dan k.

Penyelesaian:

\begin{array}{l} f (x) = h x^{3} + \frac{k}{x^{2}} = h x^{3} + k x^{- 2} \\ f ‘ (x) = 3 h x^{2} - 2 k x^{- 3} \\ f ‘ (x) = 3 h x^{2} - \frac{2 k}{x^{3}} \end{array}

Tetapi, diberi

f ‘ (x) = 12 x^{2} - \frac{258}{x^{3}}

dengan perbandingan,

3h = 12 atau 2k = 258

h = 4 atau k = 129

Soalan 12:

\begin{array}{l} Diberi y = \frac{x^{2}}{x + 3}, tunjukkan \frac{d y}{d x} = \frac{x^{2} + 6 x}{{(x + 3)}^{2}} . \\ Cari \frac{d^{2} y}{d x^{2}} dalam bentuk paling ringkas . \end{array}

Penyelesaian

\begin{array}{l} y = \frac{x^{2}}{x + 3} \\ \frac{d y}{d x} = \frac{(x + 3) (2 x) - x^{2} .1}{{(x + 3)}^{2}} = \frac{2 x^{2} + 6 x - x^{2}}{{(x + 3)}^{2}} \\ \frac{d y}{d x} = \frac{x^{2} + 6 x}{{(x + 3)}^{2}} (tertunjuk) \end{array}

\begin{array}{l} \frac{d^{2} y}{d x^{2}} = \frac{{(x + 3)}^{2} (2 x + 6) - (x^{2} + 6 x) .2 (x + 3)}{{(x + 3)}^{4}} \\ \frac{d^{2} y}{d x^{2}} = \frac{(x + 3) [(x + 3) (2 x + 6) - 2 (x^{2} + 6 x)]}{{(x + 3)}^{4}} \\ \frac{d^{2} y}{d x^{2}} = \frac{[2 x^{2} + 6 x + 6 x + 18 - 2 x^{2} - 12 x]}{{(x + 3)}^{3}} \\ \frac{d^{2} y}{d x^{2}} = \frac{18}{{(x + 3)}^{3}} \end{array}

Soalan 13:

Jika y = x² + 4x, tunjukkan

x^{2} \frac{d^{2} y}{d x^{2}} - 2 x \frac{d y}{d x} + 2 y = 0.

Penyelesaian

\begin{array}{l} y = x^{2} + 4 x \\ \frac{d y}{d x} = 2 x + 4 \\ \frac{d^{2} y}{d x^{2}} = 2 \\ x^{2} \frac{d^{2} y}{d x^{2}} - 2 x \frac{d y}{d x} + 2 y \\ = x^{2} (2) - 2 x (2 x + 4) + 2 (x^{2} + 4 x) \\ = 2 x^{2} - 4 x^{2} - 8 x + 2 x^{2} + 8 x \\ = 0 (tertunjuk) \end{array}

Soalan 14:

Diberi y = x (6 – x), ungkapkan

y \frac{d^{2} y}{d x^{2}} + x \frac{d y}{d x} + 18

dalam sebutan x yang paling ringkas.

Seterusnya, cari nilai x yang memuaskan persamaan

y \frac{d^{2} y}{d x^{2}} + x \frac{d y}{d x} + 18 = 0.

Penyelesaian:

\begin{array}{l} y = x (6 - x) = 6 x - x^{2} \\ \frac{d y}{d x} = 6 - 2 x \\ \frac{d^{2} y}{d x^{2}} = - 2 \\ ∴ y \frac{d^{2} y}{d x^{2}} + x \frac{d y}{d x} + 18 = (6 x - x^{2}) (- 2) + x (6 - 2 x) + 18 \\ = - 12 x + 2 x^{2} + 6 x - 2 x^{2} + 18 \\ = - 6 x + 18 \\ y \frac{d^{2} y}{d x^{2}} + x \frac{d y}{d x} + 18 = 0 \\ - 6 x + 18 = 0 \\ x = 3 \end{array}

Soalan 15:

Cari koordinat bagi titik pada lengkung, y = (4x – 5)² supaya kecerunan normal lengkung itu ialah ⅛.

Penyelesaian:

y = (4x – 5)²

dy/dx = 2 (4x – 5). 4 = 32x – 40

Diberi normal ialah ⅛, maka kecerunan tangen ialah –8.

dy/dx = –8

32x – 40 = –8

32x = 32

x = 1

y = [4 (1) – 5]²= 1

Hence, the coordinates of the point on the curve, y= (4x – 5)² is (1, 1).

Soalan 16:

Suatu lengkung mempunyai fungsi kecerunan kx² – 7x, dengan keadaan k ialah pemalar. Tangen kepada lengkung di titik (1, 4) adalah selari dengan garis lurus y + 2x –1 = 0.
Cari nilai k.

Penyelesaian:

Diberi fungsi kecerunan kx² – 7x selari dengan garis lurus y + 2x –1 = 0

dy/dx = kx²– 7x

y + 2x –1 = 0, y = –2x + 1, kecerunan garis lurus = –2

Maka kx²– 7x = –2

Di titik (1, 4),

k (1)²– 7(1) = –2

k – 7 = –2

k = 5

Soalan 17:

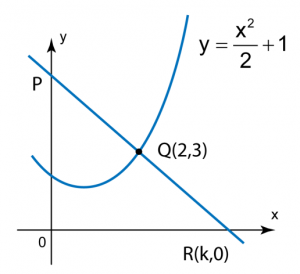
Dalam rajah di atas, garis lurus PR adalah normal kepada lengkung

y = \frac{x^{2}}{2} + 1

at Q.
Cari nilai k.

Penyelesaian:

\begin{array}{l} y = \frac{x^{2}}{2} + 1 \\ \frac{d y}{d x} = x \\ Di titik Q, koordinat- x = 2, \\ Kecerunan lengkung, \frac{d y}{d x} = 2 \\ Maka, kecerunan normal lengkung itu, \\ P R = - \frac{1}{2} \\ \frac{3 - 0}{2 - k} = - \frac{1}{2} \\ 6 = - 2 + k \\ k = 8 \end{array}

Soalan 18:

Garis normal kepada lengkung y = x² + 3x pada titik P adalah selari dengan garis lurus y = –x + 12. Cari persamaan garis normal kepada lengkung itu pada titik P.

Penyelesaian:

Diberi normal kepada lengkung di titik P adalah selari kepada garis lurus y = –x + 12. Maka, kecerunan normal lengkung itu = –1.

Seterusnya, kecerunan tangen kepada lengkung = 1

y = x² + 3x

dydx = 2x + 3

2x + 3 = 1

2x = –2

x = –1

y = (–1)²+ 3 (–1)

y = –2

Titik P = (–1, –2).

Persamaan garis normal kepada lengkung itu pada titik P ialah,

y – (–2) = –1 (x – (–1))

y + 2 = – x – 1

y = – x – 3

Soalan 19:

Diberi

y = \frac{3}{4} x^{2}

, cari perubahan kecil dalam x yang akan menyebabkan y menyusut daripada 48 kepada 47.7.

Penyelesaian:

\begin{array}{l} y = \frac{3}{4} x^{2} \\ \frac{d y}{d x} = (2) \frac{3}{4} x = \frac{3}{2} x \\ δ y = 47.7 - 48 = - 0.3 \\ perubahan kecil dalam x kepada y \\ \frac{δ x}{δ y} \approx \frac{d x}{d y} \\ δ x = \frac{d x}{d y} \times δ y \\ δ x = \frac{2}{3 x} \times (- 0.3) \\ δ x = \frac{2}{3 (8)} \times (- 0.3) \leftarrow \begin{array}{l} y = 48 \\ \frac{3}{4} x^{2} = 48 \\ x^{2} = 64 \\ x = 8 \end{array} \\ δ x = - 0.025 \end{array}

Soalan 20:

Isipada air, Icm³, dalam satu bekas diberi oleh

I = \frac{1}{5} h^{3} + 7 h

, dengan keadaan h cm ialah tinggi air dalam bekas itu. Air dituang ke dalam bekas itu dengan kadar 15cm³s^-1. Cari kadar perubahan tinggi air, dalam cms^-1, pada ketika tingginya ialah 3cm.

Penyelesaian:

\begin{array}{l} I = \frac{1}{5} h^{3} + 7 h \\ \frac{d I}{d h} = \frac{3}{5} h^{2} + 7 \\ = \frac{3 h^{2} + 35}{5} \end{array}

\begin{array}{l} Diberi \frac{d I}{d t} = 15, h = 3 \\ Kadar perubahan tinggi air = \frac{d h}{d t} \\ \frac{d h}{d t} = \frac{d h}{d I} \times \frac{d I}{d t} \leftarrow Petua rantai \\ \frac{d h}{d t} = \frac{5}{3 h^{2} + 35} \times 15 \\ \frac{d h}{d t} = \frac{75}{62} {cms}^{- 1} \end{array}

2.7.2 Pembezaan, SPM Praktis (Kertas 1 Soalan 11 – 20)

Leave a Comment Cancel reply