Soalan 11 (SPM 2019):
Rajah 1 menunjukkan sektor POQ dengan pusat O.
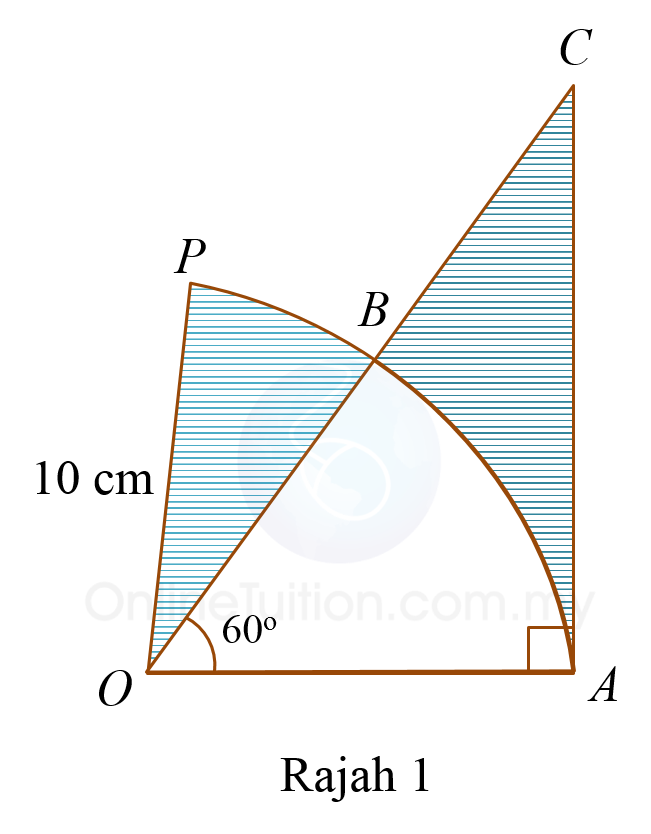
Diberi bahawa panjang lengkok PB ialah 2.56 cm. [Guna π = 3.142]
Hitung
(a) ∠ POB dalam radian, [2 markah]
(b) luas, dalam cm2, kawasan berlorek. [4 markah]
Penyelesaian:
(a)
\(\begin{array}{l} s=j \theta \\ 2.56=10 \theta \\ \theta=0.256 \text { radian } \end{array}\)
(b)
\(\begin{array}{l}\text{Luas }OBP\\=\frac12j^2\theta\\=\frac12\times10^2\times0.256\\=12.8\text{ cm}^2\\\\\frac{AC}{10}=\tan60^o\\AC=17.32\\\\\text{Luas kawasan berlorek }ABC\\={(\frac12\times10\times17.32)}-{(\frac12\times10^2\times\frac\pi3)}\\=34.233\text{ cm}^2\\\\\text{Jumlah luas kawasan berlorek}\\=12.8+34.233\\=47.033\text{ cm}^2\end{array}\)
Rajah 1 menunjukkan sektor POQ dengan pusat O.

Diberi bahawa panjang lengkok PB ialah 2.56 cm. [Guna π = 3.142]
Hitung
(a) ∠ POB dalam radian, [2 markah]
(b) luas, dalam cm2, kawasan berlorek. [4 markah]
Penyelesaian:
(a)
\(\begin{array}{l} s=j \theta \\ 2.56=10 \theta \\ \theta=0.256 \text { radian } \end{array}\)
(b)
\(\begin{array}{l}\text{Luas }OBP\\=\frac12j^2\theta\\=\frac12\times10^2\times0.256\\=12.8\text{ cm}^2\\\\\frac{AC}{10}=\tan60^o\\AC=17.32\\\\\text{Luas kawasan berlorek }ABC\\={(\frac12\times10\times17.32)}-{(\frac12\times10^2\times\frac\pi3)}\\=34.233\text{ cm}^2\\\\\text{Jumlah luas kawasan berlorek}\\=12.8+34.233\\=47.033\text{ cm}^2\end{array}\)
Soalan 12 (SPM 2020 – 6 markah):
Rajah 4 menunjukkan sebuah bekas berbentuk silinder dengan panjang 20 cm yang diletak di atas lantai dan rapat pada dinding. W ialah satu titik pada tepi tapak bekas itu. Diberi bahawa jarak titik W adalah 2 cm dari dinding dan 1 cm dari lantai.
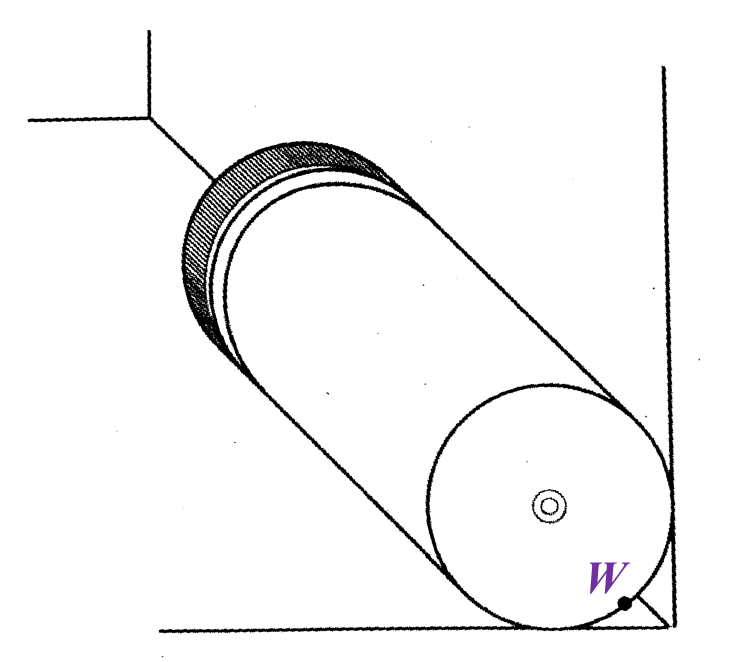
Karen ingin menyimpan bekas itu ke dalam sebuah kotak yang berukuran 21 cm × 7 cm × 7 cm.
Tentukan sama ada bekas itu boleh disimpan ke dalam kotak itu atau sebaliknya. Berikan sebab kepada jawapan anda.
Penyelesaian:

Rajah 4 menunjukkan sebuah bekas berbentuk silinder dengan panjang 20 cm yang diletak di atas lantai dan rapat pada dinding. W ialah satu titik pada tepi tapak bekas itu. Diberi bahawa jarak titik W adalah 2 cm dari dinding dan 1 cm dari lantai.

Karen ingin menyimpan bekas itu ke dalam sebuah kotak yang berukuran 21 cm × 7 cm × 7 cm.
Tentukan sama ada bekas itu boleh disimpan ke dalam kotak itu atau sebaliknya. Berikan sebab kepada jawapan anda.
Penyelesaian:

Soalan 13 (SPM 2005):
Rajah 6 menunjukkan sektor POQ bagi sebuah bulatan berpusat O. Titik A terletak pada OP, titik B terletak pada OQ dan AB berserenjang dengan OQ.
$$ \text { Panjang } O A=8 \mathrm{~cm} \text { dan } \angle P O Q=\frac{\pi}{6} \text { radian. } $$
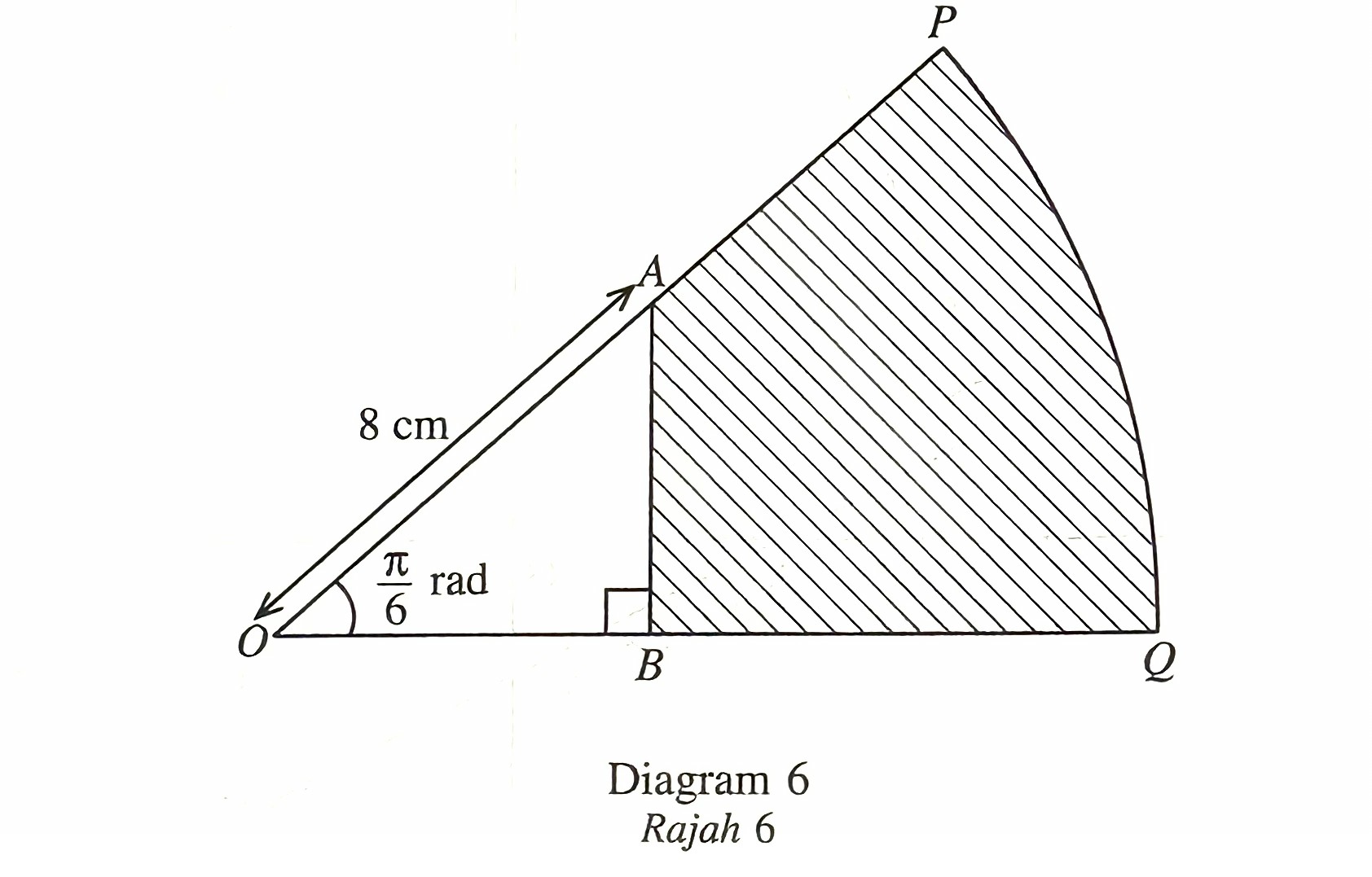
Diberi bahawa OA : OP = 4 : 7.
[Guna π = 3.142]
Hitungkan
(a) panjang, dalam cm, AP. [1 markah]
(b) perimeter, dalam cm, kawasan berlorek. [5 markah]
(c) luas, dalam cm2, kawasan berlorek. [4 markah]
Penyelesaian:
(a)
$$ A P=\frac{3}{4} \times 8 \mathrm{~cm}=6 \mathrm{~cm} $$
(b)
$$ \begin{aligned} & A B=8 \sin \frac{\pi}{6}=4 \mathrm{~cm} \\ & O Q=O P=14 \mathrm{~cm} \\ & B Q=14-8 \cos \frac{\pi}{6} \end{aligned} $$
$$ \begin{aligned} &\text { Perimeter kawasan berlorek }\\ &\begin{aligned} & =A P+A B+B Q+\operatorname{Lengkung} P Q \\ & =6+4+\left(14-8 \cos \frac{\pi}{6}\right)+14\left(\frac{\pi}{6}\right) \\ & =6+4+7.072+7.331 \\ & =24.40 \mathrm{~cm} \end{aligned} \end{aligned} $$
(c)
$$ \begin{aligned} & \text { Luas kawasan berlorek } \\ & =\text { Luas sektor } P O Q-\text { Luas } \triangle O A B \\ & =\frac{1}{2}\left(14^2\right)\left(\frac{\pi}{6}\right)-\frac{1}{2}(4)\left(8 \cos \frac{\pi}{6}\right) \\ & =37.46 \mathrm{~cm}^2 \end{aligned} $$
Rajah 6 menunjukkan sektor POQ bagi sebuah bulatan berpusat O. Titik A terletak pada OP, titik B terletak pada OQ dan AB berserenjang dengan OQ.
$$ \text { Panjang } O A=8 \mathrm{~cm} \text { dan } \angle P O Q=\frac{\pi}{6} \text { radian. } $$

Diberi bahawa OA : OP = 4 : 7.
[Guna π = 3.142]
Hitungkan
(a) panjang, dalam cm, AP. [1 markah]
(b) perimeter, dalam cm, kawasan berlorek. [5 markah]
(c) luas, dalam cm2, kawasan berlorek. [4 markah]
Penyelesaian:
(a)
$$ A P=\frac{3}{4} \times 8 \mathrm{~cm}=6 \mathrm{~cm} $$
(b)
$$ \begin{aligned} & A B=8 \sin \frac{\pi}{6}=4 \mathrm{~cm} \\ & O Q=O P=14 \mathrm{~cm} \\ & B Q=14-8 \cos \frac{\pi}{6} \end{aligned} $$
$$ \begin{aligned} &\text { Perimeter kawasan berlorek }\\ &\begin{aligned} & =A P+A B+B Q+\operatorname{Lengkung} P Q \\ & =6+4+\left(14-8 \cos \frac{\pi}{6}\right)+14\left(\frac{\pi}{6}\right) \\ & =6+4+7.072+7.331 \\ & =24.40 \mathrm{~cm} \end{aligned} \end{aligned} $$
(c)
$$ \begin{aligned} & \text { Luas kawasan berlorek } \\ & =\text { Luas sektor } P O Q-\text { Luas } \triangle O A B \\ & =\frac{1}{2}\left(14^2\right)\left(\frac{\pi}{6}\right)-\frac{1}{2}(4)\left(8 \cos \frac{\pi}{6}\right) \\ & =37.46 \mathrm{~cm}^2 \end{aligned} $$
Soalan 14 (SPM 2006):
Rajah 4 menunjukkan pelan bagi sebuah taman.
PCQ ialah semibulatan berpusat O dan mempunyai jejari 8 m.
RAQ ialah sektor bulatan berpusat A dan mempunyai jejari 14 m.
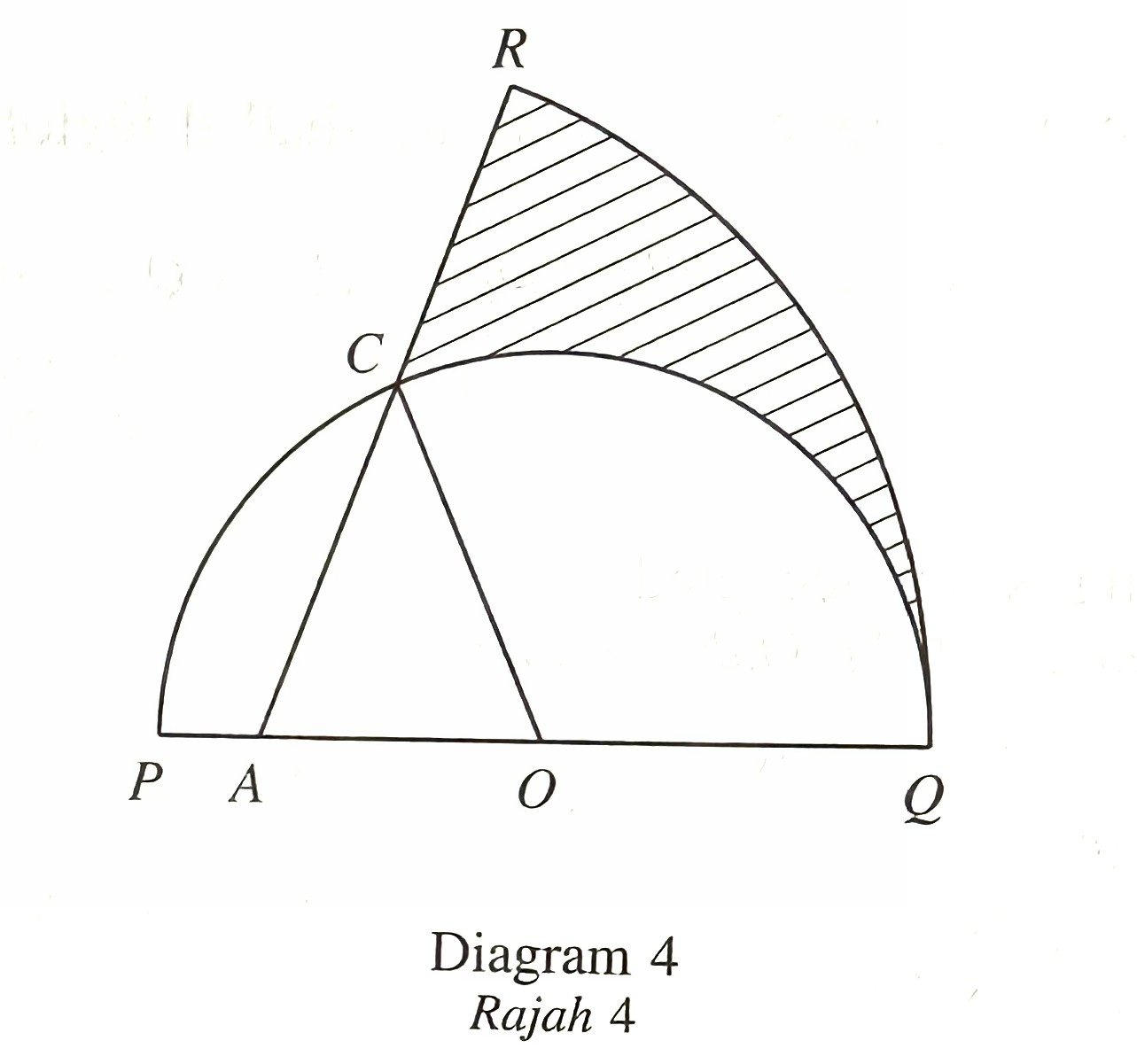
Sektor COQ ialah halaman. Kawasan berlorek ialah tapak pokok bunga dan perlu dipagar. Diberi bahawa AC = 8 m dan ∠COQ = 1.956 radian.
[Guna π = 3.142]
Hitung
(a) luas, dalam m2, halaman itu. [2 markah]
(b) panjang, dalam m, pagar yang diperlukan untuk memagari kawasan tapak pokok bunga. [4 markah]
(c) luas, dalam m2, kawasan tapak pokok bunga. [4 markah]
Penyelesaian:
(a)
$$ \begin{aligned} & \text { Luas halaman } \\ & =\text { Luas sektor } C O Q \\ & =\frac{1}{2}\left(8^2\right)(1.956) \\ & =62.59 \mathrm{~m}^2 \end{aligned} $$
(b)
$$ \begin{aligned} & A C=O C=8 \mathrm{~m} \\ & \begin{aligned} \angle C A O & =\angle C O A \\ & =3.142-1.956 \\ & =1.186 \text { radians } \end{aligned} \end{aligned} $$
$$ \begin{aligned} &R C=14-8=6 \mathrm{~m}\\ &\text { Panjang pagar yang diperlukan }\\ &\begin{aligned} & =R C+\operatorname{Lengkung} C Q+\operatorname{Lengkung} R Q \\ & =6+8(1.956)+14(1.186) \\ & =38.25 \mathrm{~m} \end{aligned} \end{aligned} $$
(c)
Luas kawasan tapak pokok bunga
= Luas sektor RAQ – Luas sektor COQ – Luas Δ CAO
$$ \begin{aligned} = & \frac{1}{2}\left(14^2\right)(1.186)-\frac{1}{2}\left(8^2\right)(1.956) \\ & -\frac{1}{2}(8)(6) \sin 1.186 \\ = & 31.39 \mathrm{~m}^2 \end{aligned} $$
Rajah 4 menunjukkan pelan bagi sebuah taman.
PCQ ialah semibulatan berpusat O dan mempunyai jejari 8 m.
RAQ ialah sektor bulatan berpusat A dan mempunyai jejari 14 m.

Sektor COQ ialah halaman. Kawasan berlorek ialah tapak pokok bunga dan perlu dipagar. Diberi bahawa AC = 8 m dan ∠COQ = 1.956 radian.
[Guna π = 3.142]
Hitung
(a) luas, dalam m2, halaman itu. [2 markah]
(b) panjang, dalam m, pagar yang diperlukan untuk memagari kawasan tapak pokok bunga. [4 markah]
(c) luas, dalam m2, kawasan tapak pokok bunga. [4 markah]
Penyelesaian:
(a)
$$ \begin{aligned} & \text { Luas halaman } \\ & =\text { Luas sektor } C O Q \\ & =\frac{1}{2}\left(8^2\right)(1.956) \\ & =62.59 \mathrm{~m}^2 \end{aligned} $$
(b)
$$ \begin{aligned} & A C=O C=8 \mathrm{~m} \\ & \begin{aligned} \angle C A O & =\angle C O A \\ & =3.142-1.956 \\ & =1.186 \text { radians } \end{aligned} \end{aligned} $$
$$ \begin{aligned} &R C=14-8=6 \mathrm{~m}\\ &\text { Panjang pagar yang diperlukan }\\ &\begin{aligned} & =R C+\operatorname{Lengkung} C Q+\operatorname{Lengkung} R Q \\ & =6+8(1.956)+14(1.186) \\ & =38.25 \mathrm{~m} \end{aligned} \end{aligned} $$
(c)
Luas kawasan tapak pokok bunga
= Luas sektor RAQ – Luas sektor COQ – Luas Δ CAO
$$ \begin{aligned} = & \frac{1}{2}\left(14^2\right)(1.186)-\frac{1}{2}\left(8^2\right)(1.956) \\ & -\frac{1}{2}(8)(6) \sin 1.186 \\ = & 31.39 \mathrm{~m}^2 \end{aligned} $$
Soalan 15 (SPM 2009):
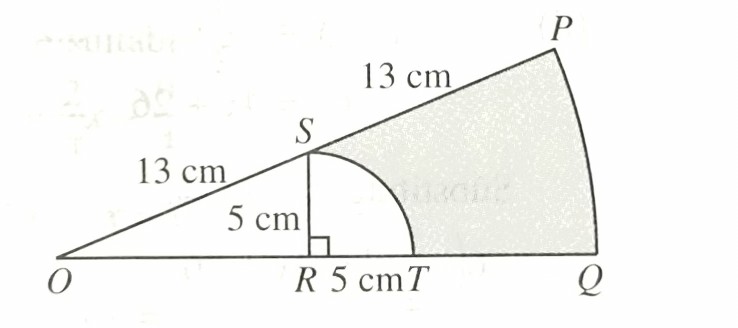
Dalam Rajah 10, POQ ialah sektor sebuah bulatan berpusat O dan berjejari 26 cm. SRT ialah suku sebuah bulatan berpusat R dan berjejari 5 cm.
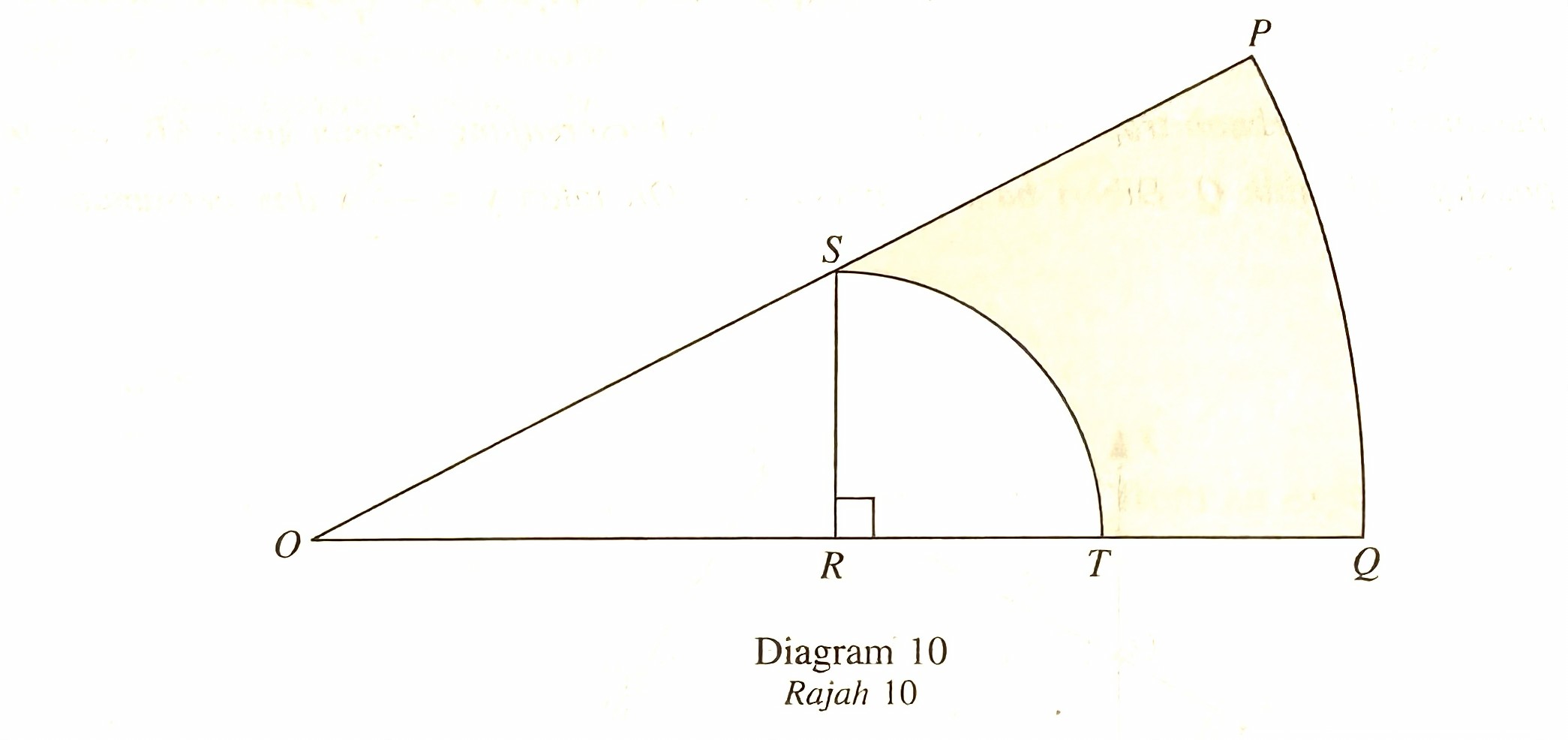
Diberi bahawa S ialah titik tengah OP.
Guna π = 3.142 dan beri jawapan betul kepada dua tempat perpuluhan.
Hitung
(a) ∠POQ, dalam radian. [2 markah]
(b) perimeter, dalam cm, kawasan berwarna. [4 markah]
(c) luas, dalam cm2, kawasan berwarna. [4 markah]
Penyelesaian:
(a)
$$ \text { Dalam } \begin{aligned} \triangle S O R, \sin \angle P O Q & =\frac{5}{13} \\ \angle P O Q & =0.39 \text { radian } \end{aligned} $$
(b)
$$ \begin{aligned} &\begin{aligned} & O R=\sqrt{13^2-5^2}=12 \mathrm{~cm} \\ & T Q=26-12-5=9 \mathrm{~cm} \end{aligned}\\ &\text { Perimeter kawasan berwarna }\\ &\begin{aligned} & =13+9+\frac{1}{4} \times 2 \pi(5)+26(0.39) \\ & =40.00 \mathrm{~cm} \end{aligned} \end{aligned} $$
(c)
$$ \begin{aligned} &\text { Luas kawasan berwarna }\\ &\begin{aligned} = & \text { Luas sektor } P O Q-\text { Luas sukuan } S R T \\ & – \text { Luas } \triangle S O R \\ = & \frac{1}{2}\left(26^2\right)(0.39)-\frac{1}{4} \times \pi\left(5^2\right)-\frac{1}{2}(12)(5) \\ = & 82.18 \mathrm{~cm}^2 \end{aligned} \end{aligned} $$
Dalam Rajah 10, POQ ialah sektor sebuah bulatan berpusat O dan berjejari 26 cm. SRT ialah suku sebuah bulatan berpusat R dan berjejari 5 cm.

Diberi bahawa S ialah titik tengah OP.
Guna π = 3.142 dan beri jawapan betul kepada dua tempat perpuluhan.
Hitung
(a) ∠POQ, dalam radian. [2 markah]
(b) perimeter, dalam cm, kawasan berwarna. [4 markah]
(c) luas, dalam cm2, kawasan berwarna. [4 markah]
Penyelesaian:

(a)
$$ \text { Dalam } \begin{aligned} \triangle S O R, \sin \angle P O Q & =\frac{5}{13} \\ \angle P O Q & =0.39 \text { radian } \end{aligned} $$
(b)
$$ \begin{aligned} &\begin{aligned} & O R=\sqrt{13^2-5^2}=12 \mathrm{~cm} \\ & T Q=26-12-5=9 \mathrm{~cm} \end{aligned}\\ &\text { Perimeter kawasan berwarna }\\ &\begin{aligned} & =13+9+\frac{1}{4} \times 2 \pi(5)+26(0.39) \\ & =40.00 \mathrm{~cm} \end{aligned} \end{aligned} $$
(c)
$$ \begin{aligned} &\text { Luas kawasan berwarna }\\ &\begin{aligned} = & \text { Luas sektor } P O Q-\text { Luas sukuan } S R T \\ & – \text { Luas } \triangle S O R \\ = & \frac{1}{2}\left(26^2\right)(0.39)-\frac{1}{4} \times \pi\left(5^2\right)-\frac{1}{2}(12)(5) \\ = & 82.18 \mathrm{~cm}^2 \end{aligned} \end{aligned} $$