Soalan 11:
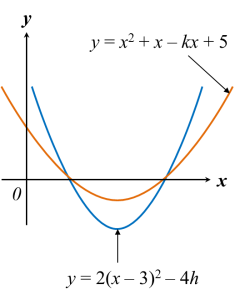
Rajah di atas menunjukkan graf lengkung y = x2 + x – kx + 5 dan y = 2(x – 3) – 4h yang bersilang pada dua titik pada paksi-x. Cari
(a) nilai k dan nilai h,
(b) nilai minimum bagi kedua-dua lengkung itu.
Penyelesaian:
(a)
(b)

Rajah di atas menunjukkan graf lengkung y = x2 + x – kx + 5 dan y = 2(x – 3) – 4h yang bersilang pada dua titik pada paksi-x. Cari
(a) nilai k dan nilai h,
(b) nilai minimum bagi kedua-dua lengkung itu.
Penyelesaian:
(a)
(b)
Soalan 12:
Fungsi kuadratik f(x) = x2 – 4px + 5p2 + 1 mempunyai nilai minimum m2 + 2p, dengan keadaan m dan p adalah pemalar.
(a) Dengan menggunakan kaedah menyempurnakan kuasa dua, tunjukkan bahawa m = p – 1.
(b) Seterusnya, atau dengan cara lain, carikan nilai p dan nilai m jika graf bagi fungsi itu bersimetri pada x = m2 – 1.
Penyelesaian:
(a)
(b)
Fungsi kuadratik f(x) = x2 – 4px + 5p2 + 1 mempunyai nilai minimum m2 + 2p, dengan keadaan m dan p adalah pemalar.
(a) Dengan menggunakan kaedah menyempurnakan kuasa dua, tunjukkan bahawa m = p – 1.
(b) Seterusnya, atau dengan cara lain, carikan nilai p dan nilai m jika graf bagi fungsi itu bersimetri pada x = m2 – 1.
Penyelesaian:
(a)
(b)
Soalan 13 (SPM 2009):
Persamaan kuadratik x2 – 5x + 6 = 0 mempunyai punca-punca h dan k, dengan keadaan h > k.
(a) Cari
(i) nilai h dan nilai k.
(ii) julat nilai x jika x2 – 5x + 6 > 0.
[5 markah]
(b) Dengan menggunakan nilai h dan nilai k dari 2 (a)(i), bentukkan persamaan kuadratik yang mempunyai punca-punca h + 2 dan 3k – 2.
[2 markah]
Penyelesaian:
(a)(i)
$$ \begin{aligned} &\begin{array}{r} x^2-5 x+6=0 \\ (x-2)(x-3)=0 \\ x=2 \text { atau } x=3 \end{array}\\ &\text { Sejak } h>k, h=3 \text { dan } k=2 \text {. } \end{aligned} $$
(a)(ii)
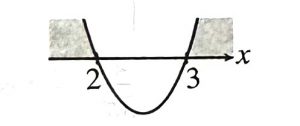
$$ \begin{array}{r} x^2-5 x+6>0 \\ (x-2)(x-3)>0 \end{array} $$ Julat adalah x < 2 atau x > 3.
(b)
$$ \begin{aligned} &\begin{aligned} & h+2=3+2=5 \\ & 3 k-2=3(2)-2=4 \end{aligned}\\ &\text { Persamaan kuadratik ialah }\\ &\begin{array}{r} x^2-(5+4) x+5(4)=0 \\ x^2-9 x+20=0 \end{array} \end{aligned} $$
Persamaan kuadratik x2 – 5x + 6 = 0 mempunyai punca-punca h dan k, dengan keadaan h > k.
(a) Cari
(i) nilai h dan nilai k.
(ii) julat nilai x jika x2 – 5x + 6 > 0.
[5 markah]
(b) Dengan menggunakan nilai h dan nilai k dari 2 (a)(i), bentukkan persamaan kuadratik yang mempunyai punca-punca h + 2 dan 3k – 2.
[2 markah]
Penyelesaian:
(a)(i)
$$ \begin{aligned} &\begin{array}{r} x^2-5 x+6=0 \\ (x-2)(x-3)=0 \\ x=2 \text { atau } x=3 \end{array}\\ &\text { Sejak } h>k, h=3 \text { dan } k=2 \text {. } \end{aligned} $$
(a)(ii)
$$ \begin{array}{r} x^2-5 x+6>0 \\ (x-2)(x-3)>0 \end{array} $$ Julat adalah x < 2 atau x > 3.

(b)
$$ \begin{aligned} &\begin{aligned} & h+2=3+2=5 \\ & 3 k-2=3(2)-2=4 \end{aligned}\\ &\text { Persamaan kuadratik ialah }\\ &\begin{array}{r} x^2-(5+4) x+5(4)=0 \\ x^2-9 x+20=0 \end{array} \end{aligned} $$