7.4 Kebarangkalian Peristiwa Tak Bersandar


7.4 Kebarangkalian Peristiwa Tak Bersandar
1.   Dua peristiwa A dan B adalah saling tak bersandar, jika kemungkinan peristiwa B berlaku tidak dipengaruhi oleh kejadian peristiwa A dan sebaliknya.

2. Jika peristiwa A dan B adalah saling tak bersandar, maka kebarangkalian peristiwa A dan B berlaku ialah

P (A ∩ B) = P (A) × P (B)

3.   Konsep kebarangkalian dua peristiwa yang tak bersandar boleh dilanjutkan kepada tiga atau lebih peristiwa yang tak bersandar. Jika A, B dan C adalah saling tak bersandar, maka
kebarangkalian peristiwa A, B dan C berlaku ialah

P (A ∩ B ∩ C) = P (A) × P (B) × P (C)

4. Masalah kebarangkalian yang melibatkan lebih daripada dua peristiwa bergabung dapat diselesaikan dengan menggunakan gambar rajah pokok.


Contoh:
Fatimah, Emily dan Rani menduduki suatu ujian lisan Bahasa Inggeris. Kebarangkalian bahawa mereka lurus ujian lisan adalah ½, ⅔  dan ¾ masing-masing. Hitung kebarangkalian bahawa 
(a) hanya seorang lurus ujian lisan,
(b) sekurang-kurangnya dua orang lurus ujian lisan,
(c) sekurang-kurangnya seorang lurus ujian lisan.

Penyelesaian:
(a)
Katakan P = Lurus dan F = Gagal
Gambar rajah pokok adalah seperti berikut.



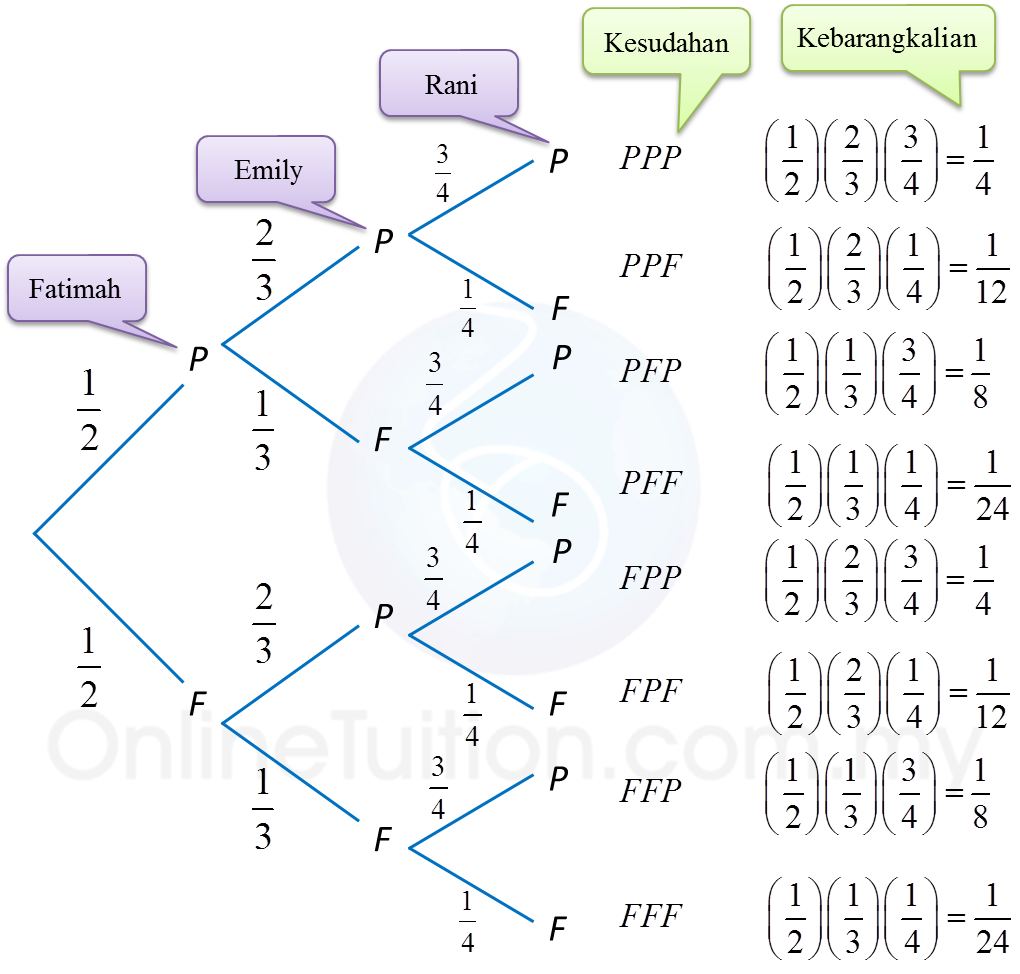
P (hanya seorang  lurus ujian lisan)
= P (PFFatau FPF atau FFP)
= P (PFF) + P (FPF) + P (FFP)
= 1 24 + 1 12 + 1 8 = 1 4  

(b)
P (sekurang-kurangnya dua orang lurus ujian lisan)
= P (PPPatau PPF atau PFP atau FPP)
= P (PPP) + P (PPF) + P (PFP) + P (FPP)
= 1 4 + 1 12 + 1 8 + 1 4 = 17 24

(c)
P (sekurang-kurangnya seorang lurus ujian lisan)
= 1 – P (semua gagal)
= 1 – P (FFF)
= 1 − 1 24 = 23 24

2 thoughts on “7.4 Kebarangkalian Peristiwa Tak Bersandar”

  1. Boleh to long selesaikan?
    Sebuah beg mengandungi 5 biji bola kuning Dan X biji bola merah. Dua biji bola dipilih secara rawak daripada beg itu. Jika kebarangkalian memilih kedua-dua bola warns merah ialah 1/6, carikan nilai X

Leave a Comment