Matematik Tambahan SPM 2017, Kertas 1 (Soalan 8 – 10)

Soalan 8 (3 markah):
Diberi bahawa hasil tambah n sebutan pertama bagi suatu janjang aritmetik ialah $S_n=\frac{n}{2}\left[13-3n\right]$  
Cari sebutan ke-n.

Penyelesaian:
$\begin{array}{l}{S}_n=\frac{n}{2}\left[13-3n\right]\\ S_{n-1}=\frac{n-1}{2}\left[13-3\left(n-1\right)\right]\\ =\frac{1}{2}\left(n-1\right)\left(13-3n+3\right)\\ =\frac{1}{2}\left(n-1\right)\left(16-3n\right)\\ \\ T_n=S_n-S_{n-1}\\ =\frac{n}{2}\left(13-3n\right)-\frac{1}{2}\left(n-1\right)\left(16-3n\right)\\ =\frac{13n}{2}-\frac{3n^2}{2}-\frac{1}{2}\left(16n-3n^2-16+3n\right)\\ =\frac{13n}{2}-\frac{3n^2}{2}-\frac{1}{2}\left(19n-3n^2-16\right)\\ =\frac{13n}{2}-\frac{3n^2}{2}-\frac{19n}{2}+\frac{3n^2}{2}+8\\ =\frac{-6n}{2}+8\\ =8-3n\end{array}$

Soalan 9 (3 markah):
Rajah 5 menunjukkan graf bagi fungsi f : x → |1 – 2x| untuk domain –2 ≤ x ≤ 4.

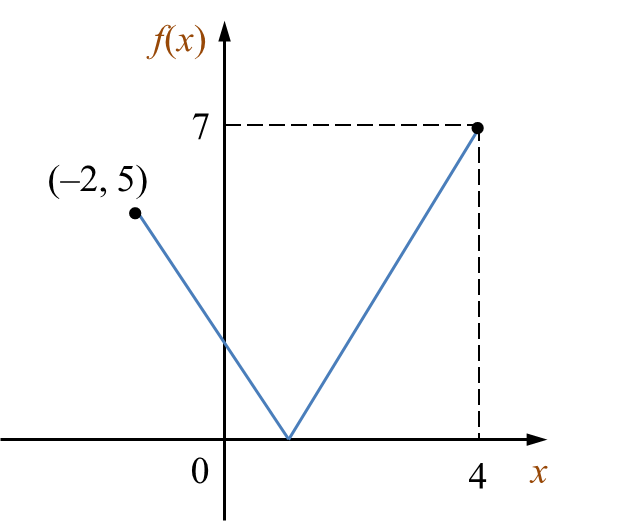Rajah 5

Nyatakan
(a) objek bagi 7,
(b) imej bagi 3,
(c) domain bagi 0 ≤ f(x) ≤ 5.


Penyelesaian:
(a)
Objek bagi 7 ialah 4.

(b)
f (x) = |1 – 2x|
f (3) = |1 – 2(3)|
= |1 – 6|
= |–5|
= 5

Imej bagi 3 ialah 5.

(c)
|1 – 2x| = 5
1 – 2x = ±5
Diberi apabila f(x) = 5, x = –2.

Apabila f(x) = –5
1 – 2x = –5
2x = 6
x = 3

Domain: –2 ≤ x ≤ 3.

Soalan 10 (4 markah):
Diberi fungsi g : x → 2x – 8, cari
$\begin{array}{l}\left(\text{a}\right)g^{-1}\left(x\right),\\ \left(\text{b}\right)\text{ nilai }p\text{ dengan keadaan }{g}^2\left(\frac{3p}{2}\right)=30.\end{array}$

Penyelesaian:
(a)
$\begin{array}{l}\text{Katakan }y=g\left(x\right)\\ =2x-8\\ 2x-8=y\\ 2x=y+8\\ x=\frac{y+8}{2}\\ \text{Maka, }{g}^{-1}\left(x\right)=\frac{x+8}{2}\end{array}$

(b)
$\begin{array}{l}g\left(x\right)=2x-8\\ g^2\left(x\right)=g\left[g\left(x\right)\right]\\ =g\left(2x-8\right)\\ =2\left(2x-8\right)-8\\ =4x-16-8\\ =4x-24\\ g^2\left(\frac{3p}{2}\right)=30\\ 4\left(\frac{3p}{2}\right)-24=30\\ 6p=54\\ p=9\end{array}$