Matematik Tambahan SPM 2017, Kertas 1 (Soalan 11 – 13)


Soalan 11 (4 markah):
Fungsi kuadratik f ditakrifkan oleh f(x) = x2 + 4x + h, dengan keadaan h ialah pemalar.
(a) Ungkapkan f(x) dalam bentuk (x + m)2 + n, dengan keadaan m dan n ialah pemalar.

(b) Diberi nilai minimum bagi f(x) ialah 8, cari nilai h.

Penyelesaian:
(a)
f(x) = x2 + 4x + h
   = x2 + 4x + (2)2 – (2)2 + h
   = (x + 2)2 – 4 + h

(b)
Diberi nilai minimum bagi f(x) = 8
– 4 + h = 8
h = 12


Soalan 12 (3 markah):
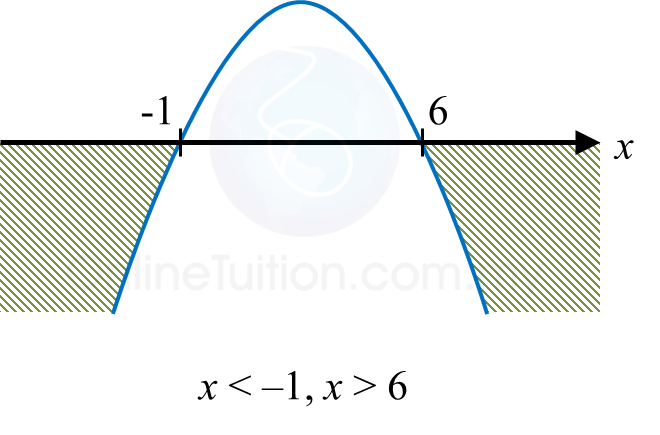
Cari julat nilai x dengan keadaan fungsi kuadratik f(x) = 6 + 5x – x2 ialah negatif.

Penyelesaian:
(a)
f(x) < 0
6 + 5x – x2 < 0
(6 – x)(x + 1) < 0
x < –1, x > 6




Soalan 13 (4 markah):
(a) Diberi bahawa satu dari punca-punca bagi persamaan kuadratik x2 + (p +3)x – p2 = 0, dengan keadaan p ialah pemalar, adalah negatif kepada yang satu lagi.
Cari nilai bagi hasil darab punca.

(b) Diberi bahawa persamaan kuadratik mx2 – 5nx + 4m = 0, dengan keadaan m dan n ialah pemalar, mempunyai dua punca yang sama.
Cari m : n.


Penyelesaian:
(a)
x2+(p+3)x–p2=0a=1, b=p+3, c=−p2Punca 1=α, Punca 2=−αHTP=−baα+(−α)=−(p+3)1−(p+3)=0p+3=0p=−3HDP=ca=−p21=−(−3)2=−9

(b)
mx2−5nx+4m=0a=m, b=−5n, c=4mb2=4ac(−5n)2=4(m)(4m)25n2=16m2m2n2=2516(mn)2=(54)2mn=54m:n=5:4

Leave a Comment