2.4 Pembezaan Peringkat Kedua, Titik Pusingan: Titik Maksimum dan Titik Minimum
(A) Pembezaan Peringkat Kedua
1. Apabila suatu fungsi y = x3 + x2 – 3x + 6 dibezakan terhadap x, terbitannya
2. Fungsi yang kedua boleh dibeza lagi terhadap x. Proses pembezaan dua kali berturut-turut ini dikenali sebagai pembezaan peringkat kedua dan ditulis sebagai .
3. Ambil perhatian bahawa .
Misalnya,
Jika y = 4x3 – 7x2 + 5x – 1,
Terbitan pertama
Terbitan kedua
(B) Titik Pusingan: Titik Maksimum dan Titik Minimum
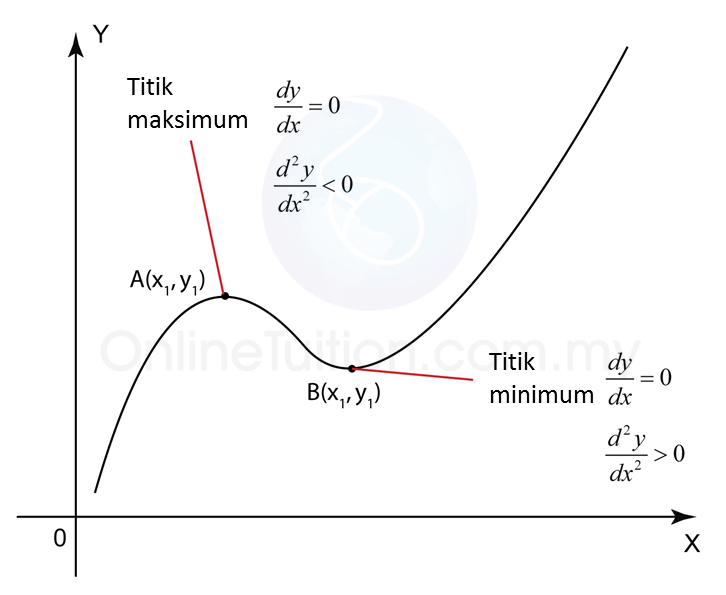

(a) Di titik pusingan A dan B,
(b) Di titik maksimum A,
(c) Di titik minimum B,
Contoh 1 (Nilai Maksimum suatu fungsi kuadratik)
Diberi bahawa y = 3x (4 – x), hitungkan
(a) nilai x apabila y adalah maksimum,
(b) nilai maksimum y.
Penyelesaian:
y = 3x (4 – x)
y = 12x – 3x2
0 = 12 – 6x
x = 2
y = 12x – 3x2
apabila x = 2,
y = 12 (2) – 3 (2)2
y = 12
Contoh 2 (Menentukan titik pusingan dan ujian terbitan kedua)
Cari koordinat titik-titik pusingan bagi lengkung y = 2x3 + 3x2 – 12x + 7 dan tentukan jenis titik itu.
Penyelesaian:
6x2 + 6x – 12 = 0
x2 + x – 2 = 0
(x – 1) (x + 2) = 0
x = 1 atau x = –2
apabila x = 1
y = 2 (1)3 + 3 (1)2 – 12 (11) + 7
y = 0
(1, 0) ialah suatu titik pusingan.
apabila x = –2
y = 2 (–2)3 + 3 (–2)2 – 12 (–2) + 7
y = 27
(-2, 27) ialah suatu titik pusingan.
ia sangat mudah untuk difahami…teruskan membuat nota seperti ini…good job…