7.8.1 Geometri Koordinat, SPM Praktis (Kertas 2)

7.8.1 Geometri Koordinat, SPM Praktis (Kertas 2)

Soalan 1:

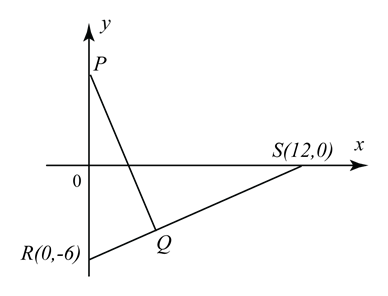
Rajah menunjukkan garis lurus PQ bertemu dengan garis lurus RS di titik Q. Titik P terletak
pada paksi-y.

(a) Tuliskan persamaan RS dalam bentuk pintasan.

(b) Diberi 2RQ = QS, cari koordinat Q.

(c) Diberi PQ berserenjang dengan RS, cari pintasan-y bagi PQ.

Penyelesaian:

(a)

\begin{array}{l} \frac{x}{12} + \frac{y}{- 6} = 1 \\ \frac{x}{12} - \frac{y}{6} = 1 \end{array}

(b)

Diberi 2RQ = QS

\begin{array}{l} \frac{R Q}{Q S} = \frac{1}{2} \\ Katakan koordinat Q = (x, y) \\ (\frac{(0) (2) + (12) (1)}{1 + 2}, \frac{(- 6) (2) + (0) (1)}{1 + 2}) = (x, y) \\ x = \frac{12}{3} = 4 \\ y = - \frac{12}{3} = - 4 \\ Q = (4, - 4) \end{array}

(c)

\begin{array}{l} Kecerunan R S, m_{R S} \\ = - (\frac{- 6}{12}) = \frac{1}{2} \\ m_{P Q} = - \frac{1}{m_{R S}} = - \frac{1}{\frac{1}{2}} = - 2 \end{array}

Titik Q = (4, –4), m = –2

Guna y = mx+ c

–4 = –2 (4) + c

c = 4

Maka, pintasan-y bagi PQ = 4

Soalan 2:

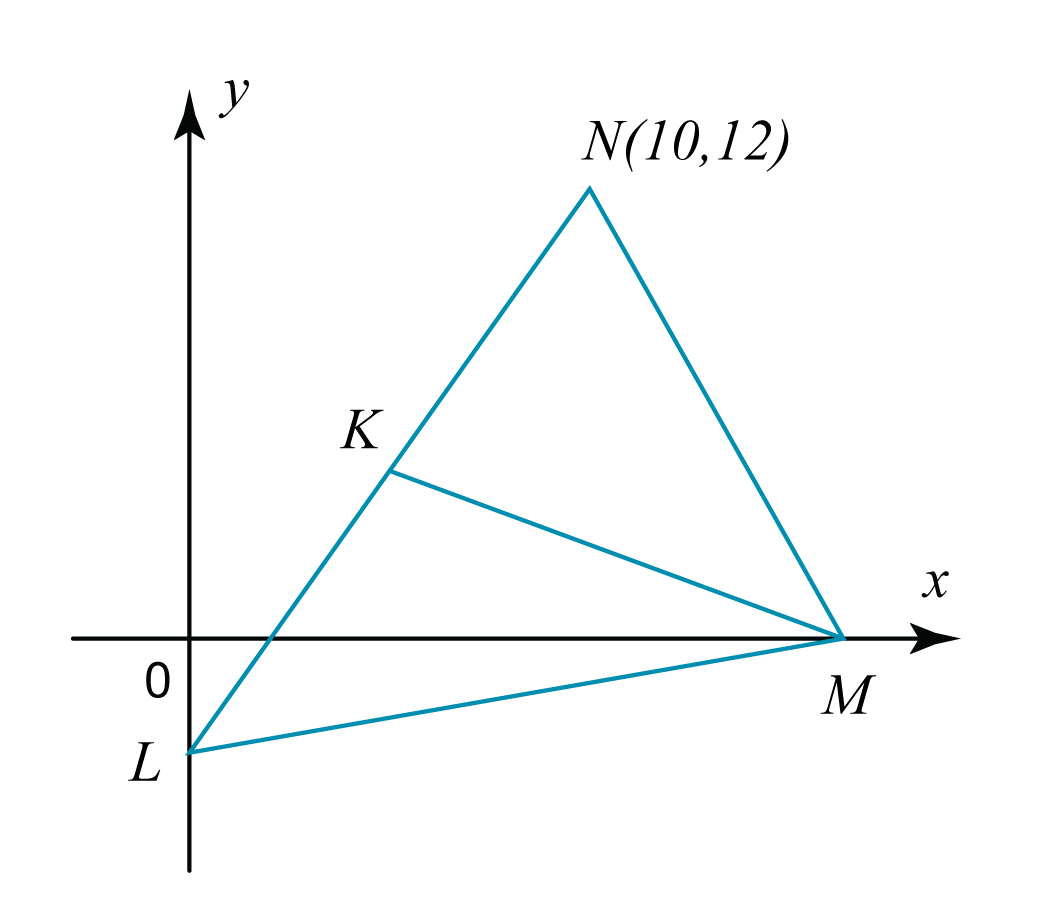
Rajah di atas menunjukkan segitiga LMN dengan keadaan L terletak di paksi-y. Persamaan garis lurus LKN dan MK adalah 2y – 3x + 6 = 0 dan 3y + x – 13 = 0 masing-masing. Cari

(a) koordinat titik K

(b) nisbah LK : KN

Penyelesaian:

(a)

2y – 3x + 6 = 0 ----(1)

3y + x – 13 = 0 ----(2)

x = 13 – 3y ----(3)

Gantikan persamaan (3) ke dalam (1),

2y – 3 (13 – 3y) + 6 = 0

2y – 39 + 9y + 6 = 0

11y = 33

y = 3

Gantikan y = 3 ke dalam persamaan (3),

x = 13 – 3 (3)

x = 4

Koordinat titik K = (4, 3).

(b)

Diberi persamaan LKN ialah 2y – 3x + 6 = 0

Di paksi-y, x = 0,

2y – 3(0) + 6 = 0

2y = –6

y = –3

koordinat titik L = (0, –3).

Nisbah LK:KN

Samakan koordinat x,

\begin{array}{l} \frac{L K (10) + K N (0)}{L K + K N} = 4 \\ 10 L K = 4 L K + 4 K N \\ 6 L K = 4 K N \\ \frac{L K}{K N} = \frac{4}{6} \\ \frac{L K}{K N} = \frac{2}{3} \end{array}

Nisbah LK : KN = 2 : 3

Leave a Comment Cancel reply