Soalan 3:
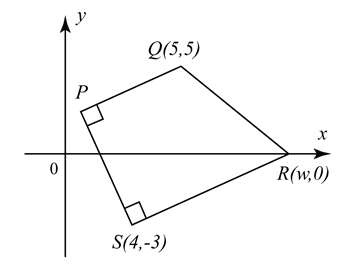
Rajah menunjukkan trapezium PQRS. Diberi persamaan PQ ialah 2y – x – 5 = 0, cari
(a) nilai w,
(b) persamaan PS dan seterusnya cari koordinat P,
(c) lokus M supaya segitiga QMS adalah sentiasa berserenjang di M.
Penyelesaian:
(a)
Persamaan PQ,
2y – x – 5 = 0
2y = x + 5
(b)
Titik S = (4, –3), m = –2
y – y1 = m (x– x1)
y – (–3) = –2 (x – 4)
y + 3 = –2x + 8
y = –2x + 5
Persamaan PS ialah y = –2x + 5
PS is y = –2x + 5-----(1)
PQ is 2y = x + 5-----(2)
Gantikan (1) ke dalam (2)
2 (–2x + 5) = x + 5
–4x + 10 = x + 5
–5x = –5
x = 1
Dari (1), y = –2(1) + 5
y = 3
Koordinat titik P = (1, 3).
(c)
Katakan M = (x, y)
Diberi ∆QMS berserenjang di M
Oleh itu, ∆QMS = 90o
(mQM) (mMS) = –1
(y – 5) (y + 3) = –1 (x– 5) (x – 4)
y2 + 3y – 5y – 15 = –1 (x2 – 4x – 5x + 20)
y2 – 2y – 15 = –x2 + 9x – 20
x2 + y2 – 9x – 2y + 5 = 0
Jadi, persamaan lokus titik M ialah
x2 + y2 – 9x – 2y + 5 = 0.
Soalan 4:
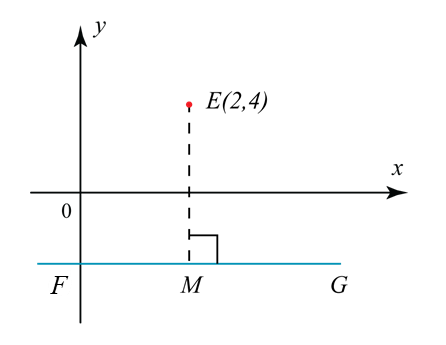
Dalam rajah di atas, persamaan bagi garis lurus FMG ialah y = – 4. Satu titik P bergerak dengan keadaan jaraknya dari E adalah sentiasa separah jarak bagi E dari garis lurus FG. Cari
(a) persamaan bagi lokus P,
(b) koordinat-x bagi titik persilangan antara lokus dengan paksi-x.
Penyelesaian:
(a)
Kecerunan garis lurus FMG = 0
EM adalah berserenjang dengan FMG, jadi kecerunan EM adalah juga = 0, persamaan EM adalah x = 2
Koordinat bagi titik M = (2, –4).
Katakan koordinat bagi titik P = (x, y).
Diberi PE = ½ EM
2PE = EM
4 (x2– 4x + 4 + y2 – 8y +16) = (0 + 64) → (Kuasa duakan kedua-dua belah)
4x2 – 16x + 16 + 4y2 – 32y + 64 = 64
4x2 + 4y2 – 16x – 32y + 16 = 0
x2 + y2 – 4x – 8y + 4 = 0
(b)
x2 + y2 – 4x – 8y + 4 = 0
pada paksi-x, y = 0.
x2 + 0 – 4x – 8(0) + 4 = 0
x2 – 4x+ 4 = 0
(x – 2) (x – 2) = 0
x = 2
Jadi, koordinat-x bagi titik persilangan antara lokus dengan paksi-x ialah 2.