Soalan 13:
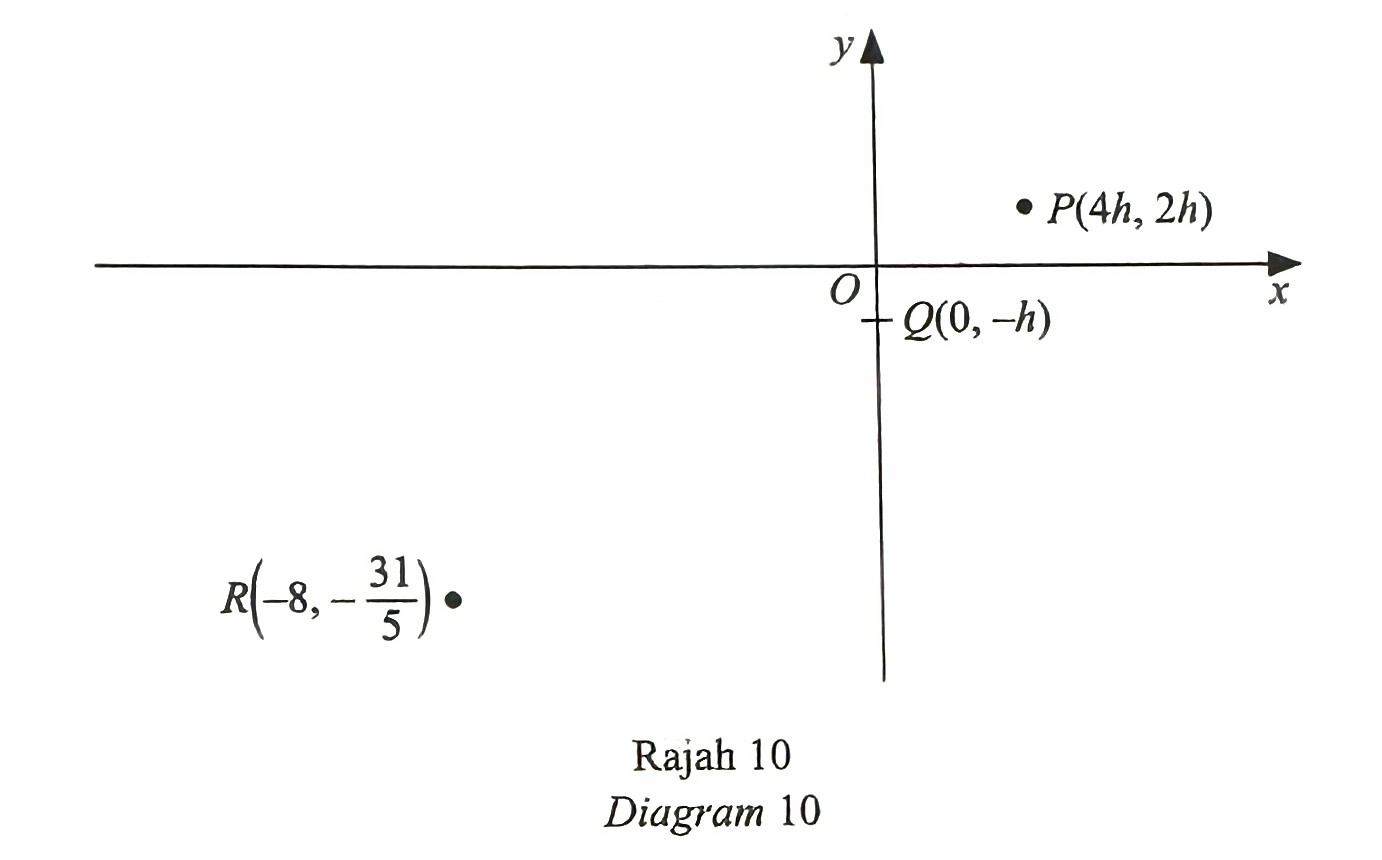
Rajah 10 menunjukkan titik-titik P, Q dan R pada suatu satah Cartes.
(a)(i)
$$ \text { Cari } \stackrel{\rightharpoonup}{P Q} \text { dalam sebutan } h \text {. } $$
(a)(ii)
$$ \text { Diberi bahawa } \stackrel{\rightharpoonup}{P Q} \text { ialah vektor unit, cari nilai } h \text {. } $$
[4 markah]
(b) Seterusnya, dengan menggunakan vektor, tunjukkan bahawa titik-titik P, Q dan R adalah segaris. [4 markah]
Jawapan:
(a)(i)
$$ \begin{aligned} & \stackrel{\rightharpoonup}{P Q}=\stackrel{\rightharpoonup}{P O}+\stackrel{\rightharpoonup}{O Q} \\ & \stackrel{\rightharpoonup}{P Q}=-\stackrel{\rightharpoonup}{O P}+\stackrel{\rightharpoonup}{O Q} \\ & \stackrel{\rightharpoonup}{P Q}=-(4 h \underline{i}+2 h \underline{j})+(-h \underline{j}) \\ & \stackrel{\rightharpoonup}{P Q}=-4 h \underline{i}-2 h \underline{j}-h \underline{j} \\ & \stackrel{\rightharpoonup}{P Q}=-4 h \underline{i}-3 h \underline{j} \end{aligned} $$
(a)(ii)
$$ \begin{aligned} \stackrel{\rightharpoonup}{P Q} & =-4 h \underline{i}-3 h \underline{j} \\ \sqrt{(-4 h)^2+(-3 h)^2} & =1 \\ \sqrt{16 h^2+9 h^2} & =1 \\ \sqrt{25 h^2} & =1 \\ h^2 & =\frac{1}{25} \\ h & = \pm \frac{1}{5} \\ \therefore h=\frac{1}{5} & \end{aligned} $$
(b)
$$ \begin{aligned} & P\left(\frac{4}{5}, \frac{2}{5}\right), Q\left(0,-\frac{1}{5}\right), R\left(-8,-\frac{31}{5}\right) \\ & \overrightarrow{Q R}=\overrightarrow{Q O}+\overrightarrow{O R} \\ & \overrightarrow{Q R}=-\overrightarrow{O Q}+\overrightarrow{O R} \\ & \overrightarrow{Q R}=-\left(-\frac{1}{5} \underline{j}\right)+\left(-8 \underline{i}-\frac{31}{5} \underline{j}\right) \\ & \overrightarrow{Q R}=\frac{1}{5} \underline{j}-8 \underline{i}-\frac{31}{5} \underline{j} \\ & \overrightarrow{Q R}=-8 \underline{i}-6 \underline{j} \end{aligned} $$
$$ \begin{aligned} & \stackrel{\rightharpoonup}{P Q}=-4 h \underline{i}-3 h \underline{j} \\ & \stackrel{\rightharpoonup}{P Q}=-\frac{4}{5} \underline{i}-\frac{3}{5} \underline{j} \\ & \stackrel{\rightharpoonup}{P Q}=\frac{1}{10}(-8 \underline{i}-6 \underline{j}) \\ & \stackrel{\rightharpoonup}{P Q}=\frac{1}{10} \stackrel{\rightharpoonup}{Q R} \end{aligned} $$
$$ \therefore \stackrel{\rightharpoonup}{P Q} \text { dan } \stackrel{\rightharpoonup}{Q R} \text { adalah selari dan } Q \text { ialah titik sepunya. Maka, } P, Q \text {, dan R adalah segaris } $$
Rajah 10 menunjukkan titik-titik P, Q dan R pada suatu satah Cartes.

(a)(i)
$$ \text { Cari } \stackrel{\rightharpoonup}{P Q} \text { dalam sebutan } h \text {. } $$
(a)(ii)
$$ \text { Diberi bahawa } \stackrel{\rightharpoonup}{P Q} \text { ialah vektor unit, cari nilai } h \text {. } $$
[4 markah]
(b) Seterusnya, dengan menggunakan vektor, tunjukkan bahawa titik-titik P, Q dan R adalah segaris. [4 markah]
Jawapan:
(a)(i)
$$ \begin{aligned} & \stackrel{\rightharpoonup}{P Q}=\stackrel{\rightharpoonup}{P O}+\stackrel{\rightharpoonup}{O Q} \\ & \stackrel{\rightharpoonup}{P Q}=-\stackrel{\rightharpoonup}{O P}+\stackrel{\rightharpoonup}{O Q} \\ & \stackrel{\rightharpoonup}{P Q}=-(4 h \underline{i}+2 h \underline{j})+(-h \underline{j}) \\ & \stackrel{\rightharpoonup}{P Q}=-4 h \underline{i}-2 h \underline{j}-h \underline{j} \\ & \stackrel{\rightharpoonup}{P Q}=-4 h \underline{i}-3 h \underline{j} \end{aligned} $$
(a)(ii)
$$ \begin{aligned} \stackrel{\rightharpoonup}{P Q} & =-4 h \underline{i}-3 h \underline{j} \\ \sqrt{(-4 h)^2+(-3 h)^2} & =1 \\ \sqrt{16 h^2+9 h^2} & =1 \\ \sqrt{25 h^2} & =1 \\ h^2 & =\frac{1}{25} \\ h & = \pm \frac{1}{5} \\ \therefore h=\frac{1}{5} & \end{aligned} $$
(b)
$$ \begin{aligned} & P\left(\frac{4}{5}, \frac{2}{5}\right), Q\left(0,-\frac{1}{5}\right), R\left(-8,-\frac{31}{5}\right) \\ & \overrightarrow{Q R}=\overrightarrow{Q O}+\overrightarrow{O R} \\ & \overrightarrow{Q R}=-\overrightarrow{O Q}+\overrightarrow{O R} \\ & \overrightarrow{Q R}=-\left(-\frac{1}{5} \underline{j}\right)+\left(-8 \underline{i}-\frac{31}{5} \underline{j}\right) \\ & \overrightarrow{Q R}=\frac{1}{5} \underline{j}-8 \underline{i}-\frac{31}{5} \underline{j} \\ & \overrightarrow{Q R}=-8 \underline{i}-6 \underline{j} \end{aligned} $$
$$ \begin{aligned} & \stackrel{\rightharpoonup}{P Q}=-4 h \underline{i}-3 h \underline{j} \\ & \stackrel{\rightharpoonup}{P Q}=-\frac{4}{5} \underline{i}-\frac{3}{5} \underline{j} \\ & \stackrel{\rightharpoonup}{P Q}=\frac{1}{10}(-8 \underline{i}-6 \underline{j}) \\ & \stackrel{\rightharpoonup}{P Q}=\frac{1}{10} \stackrel{\rightharpoonup}{Q R} \end{aligned} $$
$$ \therefore \stackrel{\rightharpoonup}{P Q} \text { dan } \stackrel{\rightharpoonup}{Q R} \text { adalah selari dan } Q \text { ialah titik sepunya. Maka, } P, Q \text {, dan R adalah segaris } $$