Soalan 11:
(a) Terdapat (n + 1) titik pada lilitan sebuah bulatan. Jika setiap titik disambungkan dengan garis lurus ke semua titik-titik yang lain, terdapat 4n garis lurus yang terbentuk.
Poligon boleh dibentuk dengan menyambungkan titik-titik pada lilitan bulatan itu.
Cari jumlah bilangan poligon yang mungkin.
[4 markah]
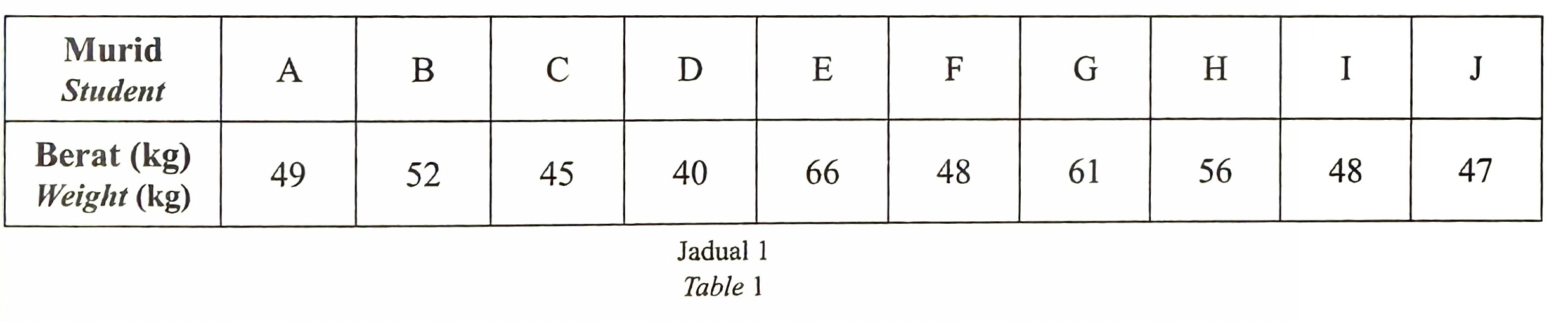
(b) Sebuah dormitori mempunyai 5 buah katil dua tingkat. Setiap katil dua tingkat mempunyai satu katil atas dan satu katil bawah. Jadual 1 menunjukkan berat bagi 10 orang murid lelaki yang akan ditempatkan di dalam dormitori itu. Murid A dan murid B adalah pasangan kembar.
Cari bilangan cara berbeza untuk menyusun jika
(i) tiada syarat dikenakan,
(ii) murid-murid dengan berat melebihi 50 kg ditempatkan di katil bawah dan pasangan kembar ditempatkan di sebuah katil dua tingkat yang sama.
[4 markah]
Jawapan:
(a)
$$ \begin{aligned} { }^{n+1} C_2 & =4 n \\ \frac{(n+1)!}{2![(n+1)-2]!} & =4 n \\ \frac{(n+1)!}{2!(n-1)!} & =4 n \\ \frac{(n+1)(n)(n-1)!}{2!(n-1)!} & =4 n \\ \frac{n(n+1)}{2} & =4 n \\ n^2+n & =8 n \\ n^2+n-8 n & =0 \\ n^2-7 n & =0 \\ n(n-7) & =0 \\ n=0 \quad ; \quad n-7 & =0 \\ n & =7 \\ \therefore n=7 \quad & \end{aligned} $$
$$ \begin{aligned} &\text { Jumlah bilangan poligon }\\ &\begin{aligned} & ={ }^7 C_3+{ }^7 C_4+{ }^7 C_5+{ }^7 C_6+{ }^7 C_7 \\ & =35+35+21+7+1 \\ & =99 \end{aligned} \end{aligned} $$
(b)(i)
$$ \begin{aligned} \text { Bilangan cara } & ={ }^{10} P_{10} \\ & =3628800 \end{aligned} $$
(b)(ii)
$$ \begin{aligned} & >50 \rightarrow B, E, G, H \\ & <50 \rightarrow A, C, D, F, I, J \end{aligned} $$
$$ \begin{aligned} \text { Bilangan cara } & ={ }^5 P_1 \times{ }^4 P_3 \times{ }^5 P_5 \\ & =5 \times 24 \times 120 \\ & =14400 \end{aligned} $$
(a) Terdapat (n + 1) titik pada lilitan sebuah bulatan. Jika setiap titik disambungkan dengan garis lurus ke semua titik-titik yang lain, terdapat 4n garis lurus yang terbentuk.
Poligon boleh dibentuk dengan menyambungkan titik-titik pada lilitan bulatan itu.
Cari jumlah bilangan poligon yang mungkin.
[4 markah]
(b) Sebuah dormitori mempunyai 5 buah katil dua tingkat. Setiap katil dua tingkat mempunyai satu katil atas dan satu katil bawah. Jadual 1 menunjukkan berat bagi 10 orang murid lelaki yang akan ditempatkan di dalam dormitori itu. Murid A dan murid B adalah pasangan kembar.

Cari bilangan cara berbeza untuk menyusun jika
(i) tiada syarat dikenakan,
(ii) murid-murid dengan berat melebihi 50 kg ditempatkan di katil bawah dan pasangan kembar ditempatkan di sebuah katil dua tingkat yang sama.
[4 markah]
Jawapan:
(a)
$$ \begin{aligned} { }^{n+1} C_2 & =4 n \\ \frac{(n+1)!}{2![(n+1)-2]!} & =4 n \\ \frac{(n+1)!}{2!(n-1)!} & =4 n \\ \frac{(n+1)(n)(n-1)!}{2!(n-1)!} & =4 n \\ \frac{n(n+1)}{2} & =4 n \\ n^2+n & =8 n \\ n^2+n-8 n & =0 \\ n^2-7 n & =0 \\ n(n-7) & =0 \\ n=0 \quad ; \quad n-7 & =0 \\ n & =7 \\ \therefore n=7 \quad & \end{aligned} $$
$$ \begin{aligned} &\text { Jumlah bilangan poligon }\\ &\begin{aligned} & ={ }^7 C_3+{ }^7 C_4+{ }^7 C_5+{ }^7 C_6+{ }^7 C_7 \\ & =35+35+21+7+1 \\ & =99 \end{aligned} \end{aligned} $$
(b)(i)
$$ \begin{aligned} \text { Bilangan cara } & ={ }^{10} P_{10} \\ & =3628800 \end{aligned} $$
(b)(ii)
$$ \begin{aligned} & >50 \rightarrow B, E, G, H \\ & <50 \rightarrow A, C, D, F, I, J \end{aligned} $$
$$ \begin{aligned} \text { Bilangan cara } & ={ }^5 P_1 \times{ }^4 P_3 \times{ }^5 P_5 \\ & =5 \times 24 \times 120 \\ & =14400 \end{aligned} $$
Soalan 12:
Rajah 9 menunjukkan enam keping kad huruf yang digunakan dalam suatu eksperimen Binomial.

Satu kad akan dipilih secara rawak dalam setiap percubaan Bernoulli. Kad itu kemudiannya dikembalikan.
(a) Jika terdapat 120 percubaan, cari nilai jangkaan bilangan kad huruf konsonan yang akan dipilih. [2 markah]
(b) Jika terdapat 5 percubaan, cari kebarangkalian bahawa bilangan kad huruf konsonan yang terpilih adalah melebihi bilangan kad huruf vokal yang terpilih. [4 markah]
Jawapan:
(a)
$$ \begin{aligned} & \text { Konsonan } =C, R, D, K \\ & \text { Vokal } =E, I \end{aligned} $$
$$ \begin{aligned} P(\text { Konsonan } ) & =\frac{4}{6} \\ & =\frac{2}{3} \end{aligned} $$
$$ \begin{aligned} \text { Jangkaan bilangan } & =(120)\left(\frac{2}{3}\right) \\ & =80 \end{aligned} $$
(b)
$$ \begin{aligned} & \text { Katakan } X=\text { Konsonan } \\ & \begin{aligned} P(X>2) & =P(X=3)+P(X=4)+P(X=5) \\ & ={ }^5 C_3\left(\frac{2}{3}\right)^3\left(\frac{1}{3}\right)^2+{ }^5 C_4\left(\frac{2}{3}\right)^4\left(\frac{1}{3}\right)^1+{ }^5 C_5\left(\frac{2}{3}\right)^5\left(\frac{1}{3}\right)^0 \\ & =0.3292+0.3292+0.1317 \\ & =0.7901 \end{aligned} \end{aligned} $$
Rajah 9 menunjukkan enam keping kad huruf yang digunakan dalam suatu eksperimen Binomial.

Satu kad akan dipilih secara rawak dalam setiap percubaan Bernoulli. Kad itu kemudiannya dikembalikan.
(a) Jika terdapat 120 percubaan, cari nilai jangkaan bilangan kad huruf konsonan yang akan dipilih. [2 markah]
(b) Jika terdapat 5 percubaan, cari kebarangkalian bahawa bilangan kad huruf konsonan yang terpilih adalah melebihi bilangan kad huruf vokal yang terpilih. [4 markah]
Jawapan:
(a)
$$ \begin{aligned} & \text { Konsonan } =C, R, D, K \\ & \text { Vokal } =E, I \end{aligned} $$
$$ \begin{aligned} P(\text { Konsonan } ) & =\frac{4}{6} \\ & =\frac{2}{3} \end{aligned} $$
$$ \begin{aligned} \text { Jangkaan bilangan } & =(120)\left(\frac{2}{3}\right) \\ & =80 \end{aligned} $$
(b)
$$ \begin{aligned} & \text { Katakan } X=\text { Konsonan } \\ & \begin{aligned} P(X>2) & =P(X=3)+P(X=4)+P(X=5) \\ & ={ }^5 C_3\left(\frac{2}{3}\right)^3\left(\frac{1}{3}\right)^2+{ }^5 C_4\left(\frac{2}{3}\right)^4\left(\frac{1}{3}\right)^1+{ }^5 C_5\left(\frac{2}{3}\right)^5\left(\frac{1}{3}\right)^0 \\ & =0.3292+0.3292+0.1317 \\ & =0.7901 \end{aligned} \end{aligned} $$