Soalan 1:
Rajah 1 menunjukkan graf garis lurus yang diperoleh apabila y = 4x2 – 5 ditukarkan dalam bentuk linear.

Ungkapkan X dan Y dalam sebutan x dan / atau y.
[2 markah]
Jawapan:
$$ \begin{aligned} & \left(y=4 x^2-5\right) \div x^2 \\ & \frac{y}{x^2}=4-\frac{5}{x^2} \\ & \frac{y}{x^2}=-5\left(\frac{1}{x^2}\right)+4 \\ & \boldsymbol{Y}=\boldsymbol{m} \quad \boldsymbol{X}+\boldsymbol{C} \\ & Y=\frac{y}{x^2} \\ & X=\frac{1}{x^2} \end{aligned} $$
Rajah 1 menunjukkan graf garis lurus yang diperoleh apabila y = 4x2 – 5 ditukarkan dalam bentuk linear.

Ungkapkan X dan Y dalam sebutan x dan / atau y.
[2 markah]
Jawapan:
$$ \begin{aligned} & \left(y=4 x^2-5\right) \div x^2 \\ & \frac{y}{x^2}=4-\frac{5}{x^2} \\ & \frac{y}{x^2}=-5\left(\frac{1}{x^2}\right)+4 \\ & \boldsymbol{Y}=\boldsymbol{m} \quad \boldsymbol{X}+\boldsymbol{C} \\ & Y=\frac{y}{x^2} \\ & X=\frac{1}{x^2} \end{aligned} $$
Soalan 2:
(a) Rajah 2 menunjukkan hubungan bagi dua set.
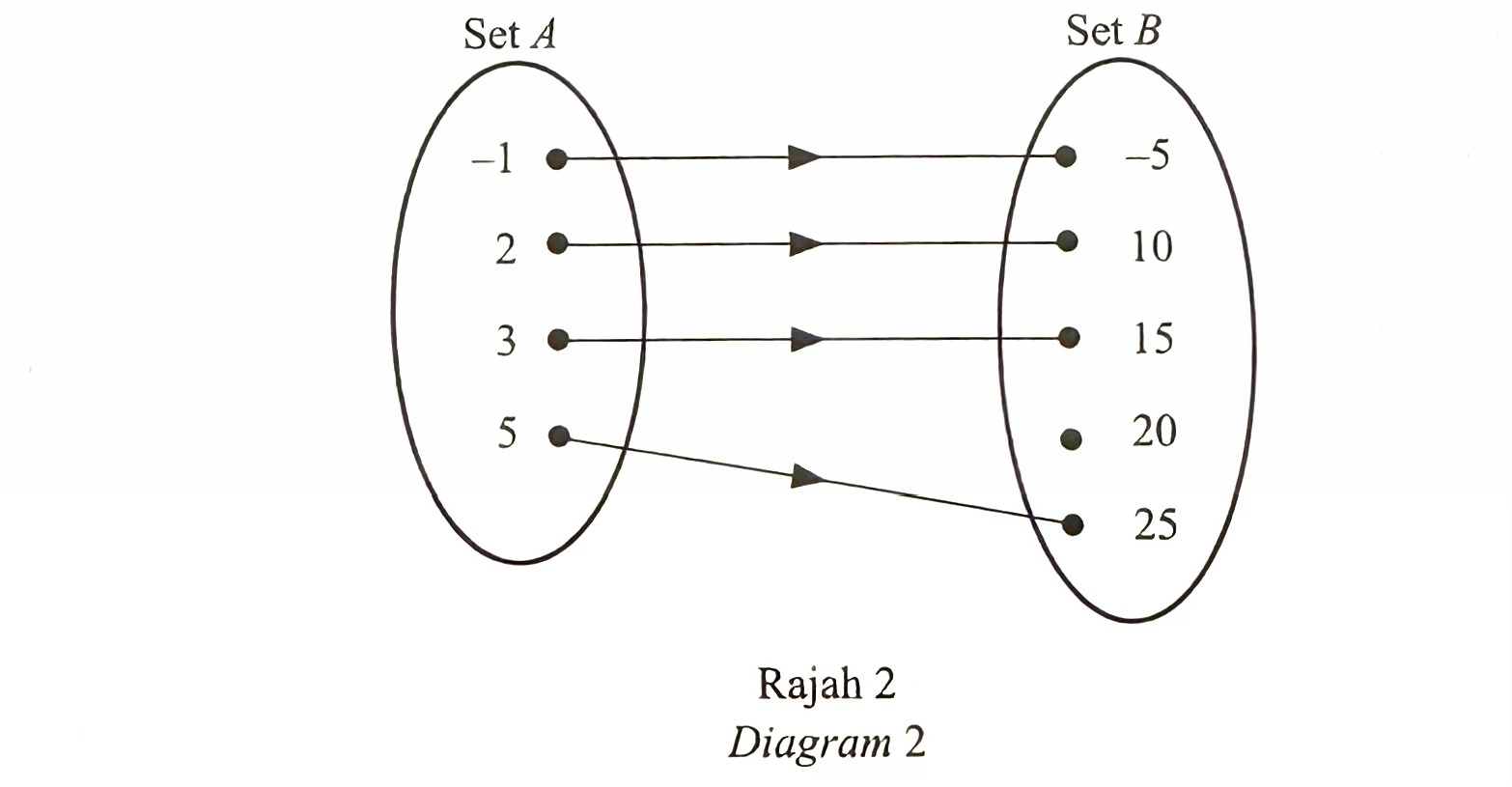
Nyatakan julat hubungan itu. [1 markah]
(b) Fungsi g(x) = 3 – x diungkapkan dalam bentuk pasangan tertib seperti di bawah:
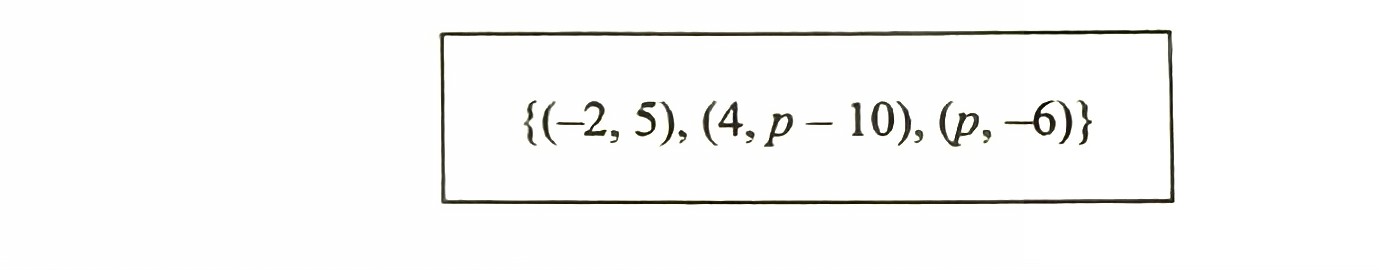 Cari nilai p.
Cari nilai p.
[2 markah]
Jawapan:
(a) {-5, 10, 15, 25}
(b)
$$ \begin{aligned} g(x) & =3-x \\ g(4) & =p-10 \\ 3-4 & =p-10 \\ -1 & =p-10 \\ -1+10 & =p \\ p & =9 \end{aligned} $$
(a) Rajah 2 menunjukkan hubungan bagi dua set.

Nyatakan julat hubungan itu. [1 markah]
(b) Fungsi g(x) = 3 – x diungkapkan dalam bentuk pasangan tertib seperti di bawah:
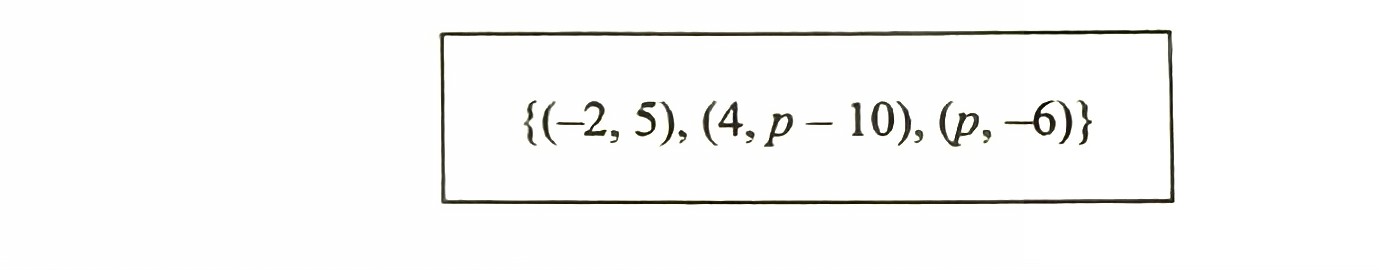 Cari nilai p.
Cari nilai p.[2 markah]
Jawapan:
(a) {-5, 10, 15, 25}
(b)
$$ \begin{aligned} g(x) & =3-x \\ g(4) & =p-10 \\ 3-4 & =p-10 \\ -1 & =p-10 \\ -1+10 & =p \\ p & =9 \end{aligned} $$