Soalan 3:
(a)
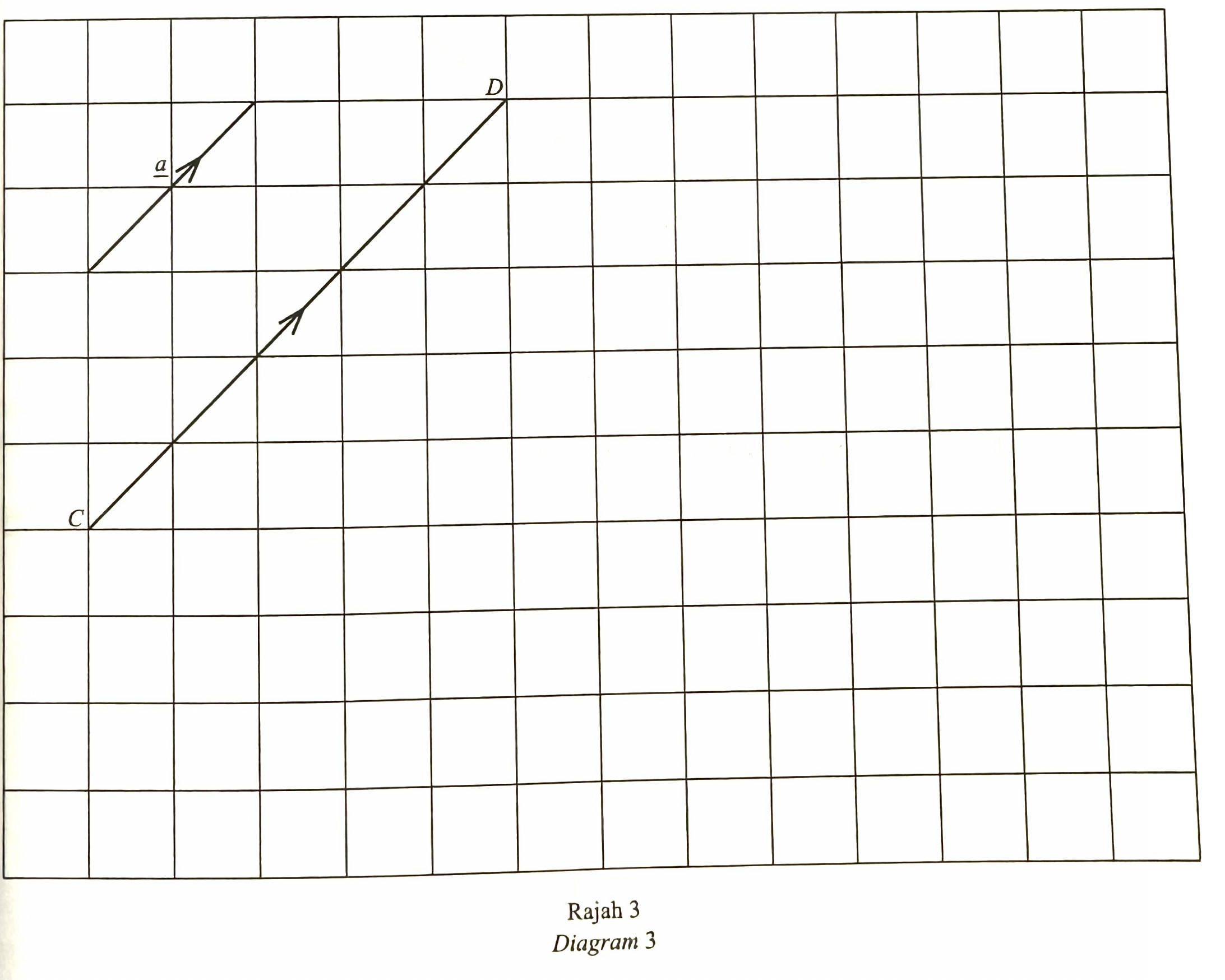
$$ \text { Rajah } 3 \text { menunjukkan } \underline{a} \text { dan } \stackrel{\rightharpoonup}{C D} \text { pada grid segi empat sama. } $$
 (i)
(i)
$$ \text { Ungkapkan } \stackrel{\rightharpoonup}{C D} \text { dalam sebutan } \underline{a} \text {. } $$
(ii)
$$ \text { Lukis }-4 \underline{a} \text { pada Rajah } 3 . $$
[2 markah]
(b) Penyelesaian secara lukisan berskala dan / atau vektor tidak diterima.
Rajah 4 menunjukkan garis lurus AB.
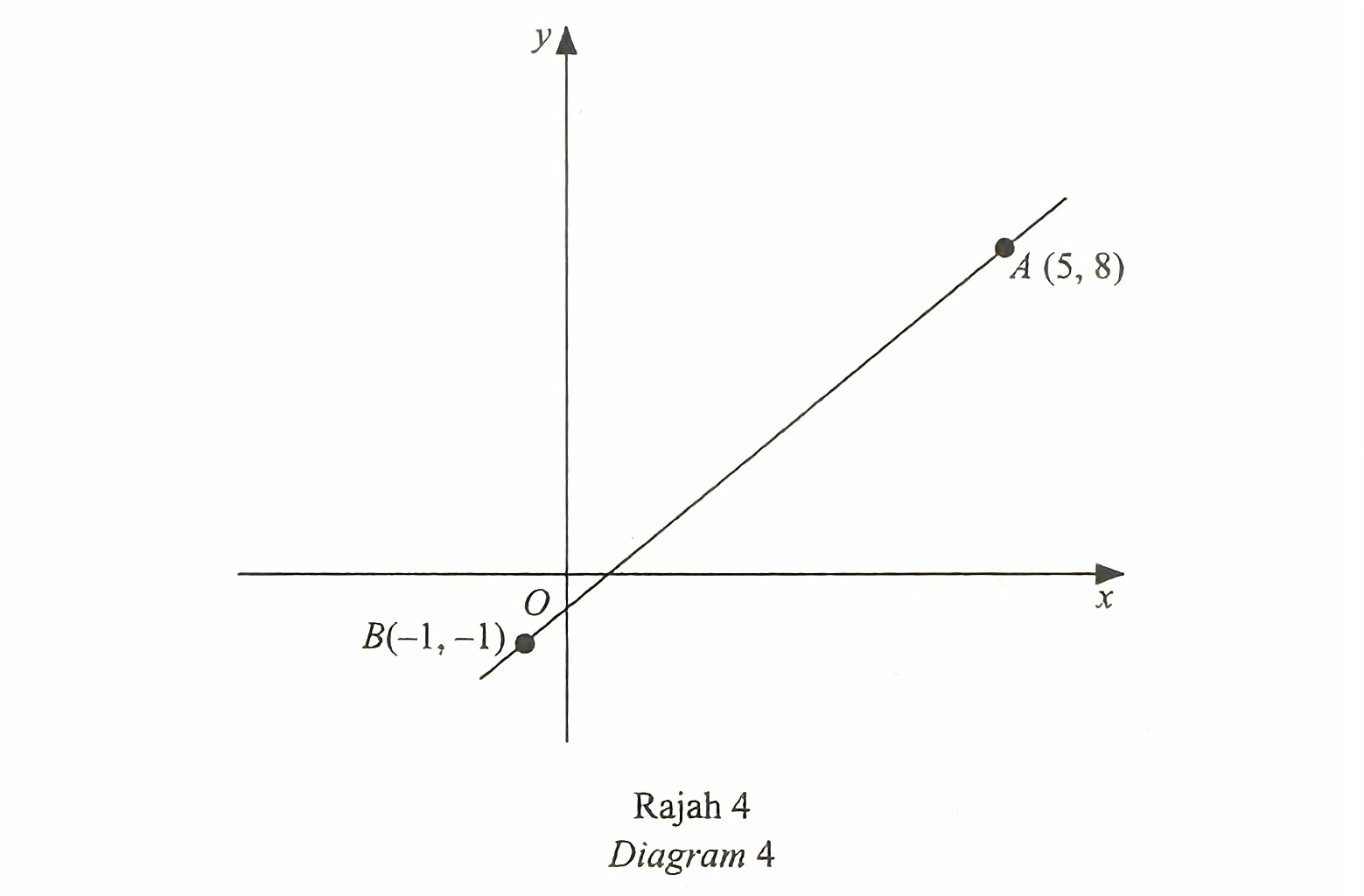
Diberi bahawa titik C terletak pada AB dengan keadaan AC : CB = 2 : 1, cari koordinat C.
[2 markah]
(c) Penyelesaian secara lukisan berskala tidak diterima.
Diberi bahawa P(4, 5) dan Q(2, 1) terletak pada suatu satah Cartes.
Cari persamaan garis lurus yang berserenjang dengan garis lurus PQ dan melalui titik P.
[3 markah]
Jawapan:
(a)(i)
$$ \begin{aligned} & \overrightarrow{C D}=\underline{a}+\underline{a}+\frac{1}{2} \underline{a} \\ & \overrightarrow{C D}=\frac{5}{2} \underline{a} \end{aligned} $$
(a)(ii)
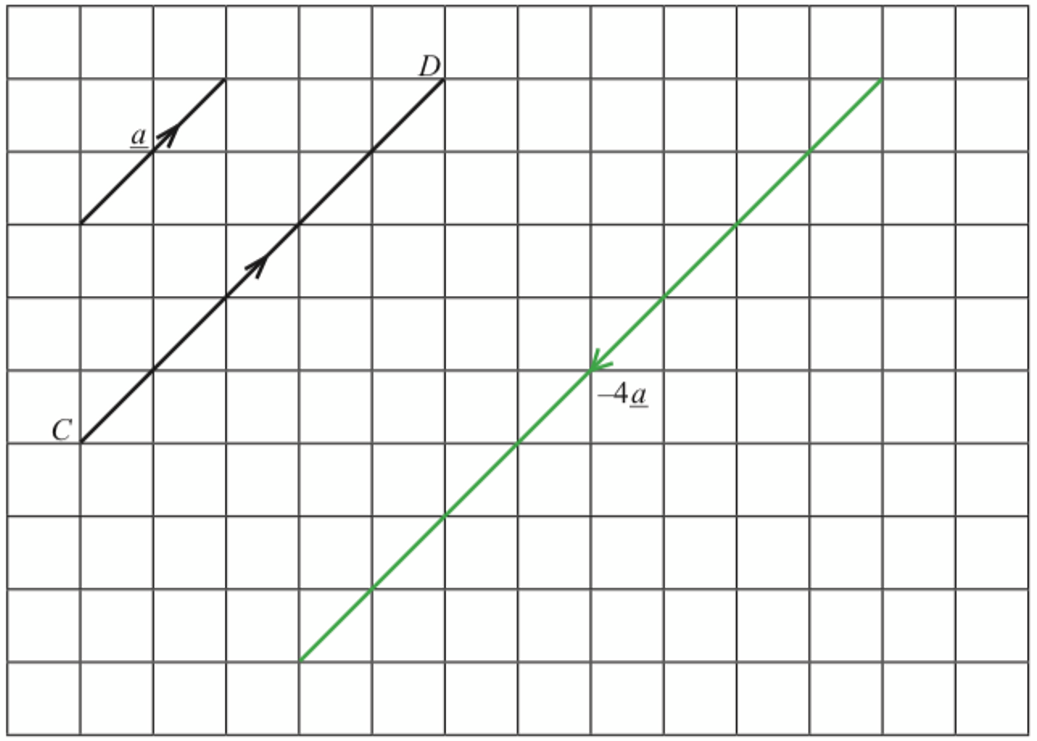
(b)
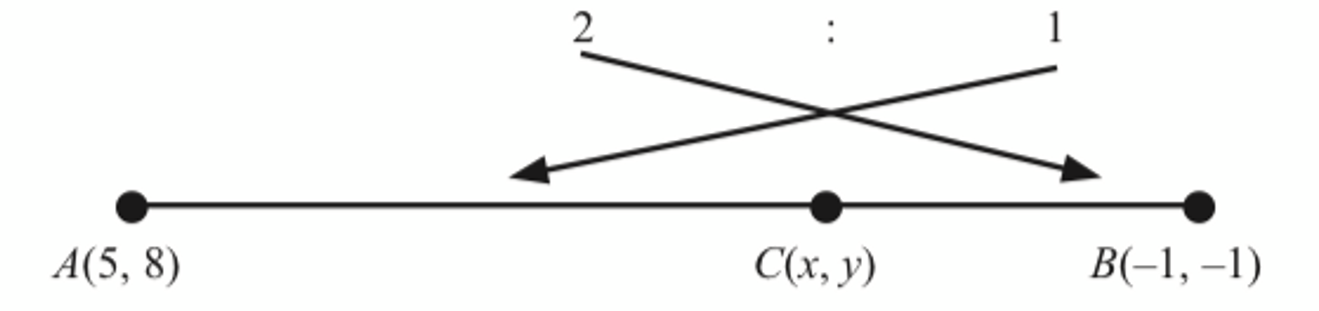
$$ \begin{aligned} C(x, y) & =\left(\frac{2(-1)+(1)(5)}{2+1}, \frac{(2)(-1)+(1)(8)}{2+1}\right) \\ & =(1,2) \end{aligned} $$
(c)
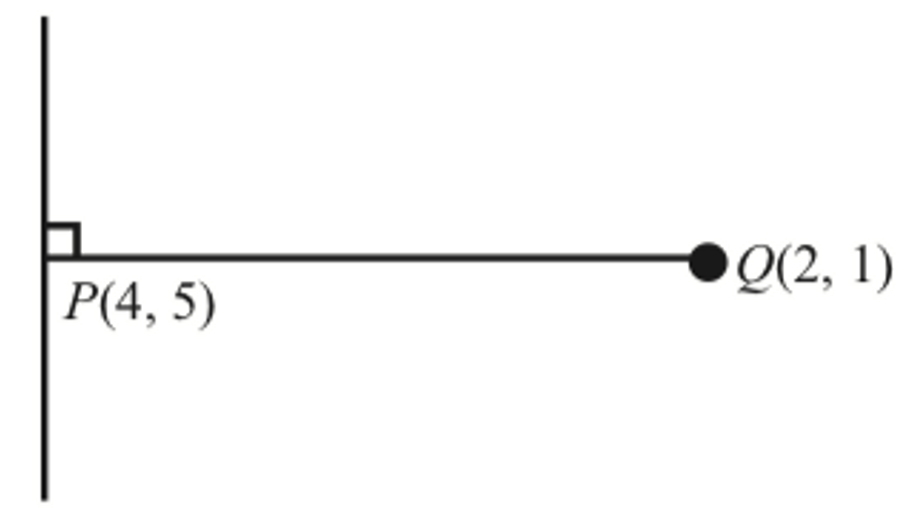
$$ \begin{aligned} m_{P Q} & =\frac{5-1}{4-2} \\ & =2 \end{aligned} $$
$$ \begin{aligned} m_{P Q} \times m_2 & =-1 \\ 2 \times m_2 & =-1 \\ m_2 & =-\frac{1}{2} \end{aligned} $$
$$ \begin{aligned} y-y_1 & =m\left(x-x_1\right) \\ y-5 & =-\frac{1}{2}(x-4) \\ y & =-\frac{1}{2} x+2+5 \\ y & =-\frac{1}{2} x+7 \end{aligned} $$
(a)
$$ \text { Rajah } 3 \text { menunjukkan } \underline{a} \text { dan } \stackrel{\rightharpoonup}{C D} \text { pada grid segi empat sama. } $$
 (i)
(i)$$ \text { Ungkapkan } \stackrel{\rightharpoonup}{C D} \text { dalam sebutan } \underline{a} \text {. } $$
(ii)
$$ \text { Lukis }-4 \underline{a} \text { pada Rajah } 3 . $$
[2 markah]
(b) Penyelesaian secara lukisan berskala dan / atau vektor tidak diterima.
Rajah 4 menunjukkan garis lurus AB.

Diberi bahawa titik C terletak pada AB dengan keadaan AC : CB = 2 : 1, cari koordinat C.
[2 markah]
(c) Penyelesaian secara lukisan berskala tidak diterima.
Diberi bahawa P(4, 5) dan Q(2, 1) terletak pada suatu satah Cartes.
Cari persamaan garis lurus yang berserenjang dengan garis lurus PQ dan melalui titik P.
[3 markah]
Jawapan:
(a)(i)
$$ \begin{aligned} & \overrightarrow{C D}=\underline{a}+\underline{a}+\frac{1}{2} \underline{a} \\ & \overrightarrow{C D}=\frac{5}{2} \underline{a} \end{aligned} $$
(a)(ii)

(b)

$$ \begin{aligned} C(x, y) & =\left(\frac{2(-1)+(1)(5)}{2+1}, \frac{(2)(-1)+(1)(8)}{2+1}\right) \\ & =(1,2) \end{aligned} $$
(c)

$$ \begin{aligned} m_{P Q} & =\frac{5-1}{4-2} \\ & =2 \end{aligned} $$
$$ \begin{aligned} m_{P Q} \times m_2 & =-1 \\ 2 \times m_2 & =-1 \\ m_2 & =-\frac{1}{2} \end{aligned} $$
$$ \begin{aligned} y-y_1 & =m\left(x-x_1\right) \\ y-5 & =-\frac{1}{2}(x-4) \\ y & =-\frac{1}{2} x+2+5 \\ y & =-\frac{1}{2} x+7 \end{aligned} $$
Soalan 4:
Rajah 5 menunjukkan sebuah bulatan dengan pusat O dan lengkok AB yang mencangkum sudut θ rad pada O. Diberi bahawa jejari bulatan itu ialah j unit dan panjang lengkok minor AB ialah s unit.
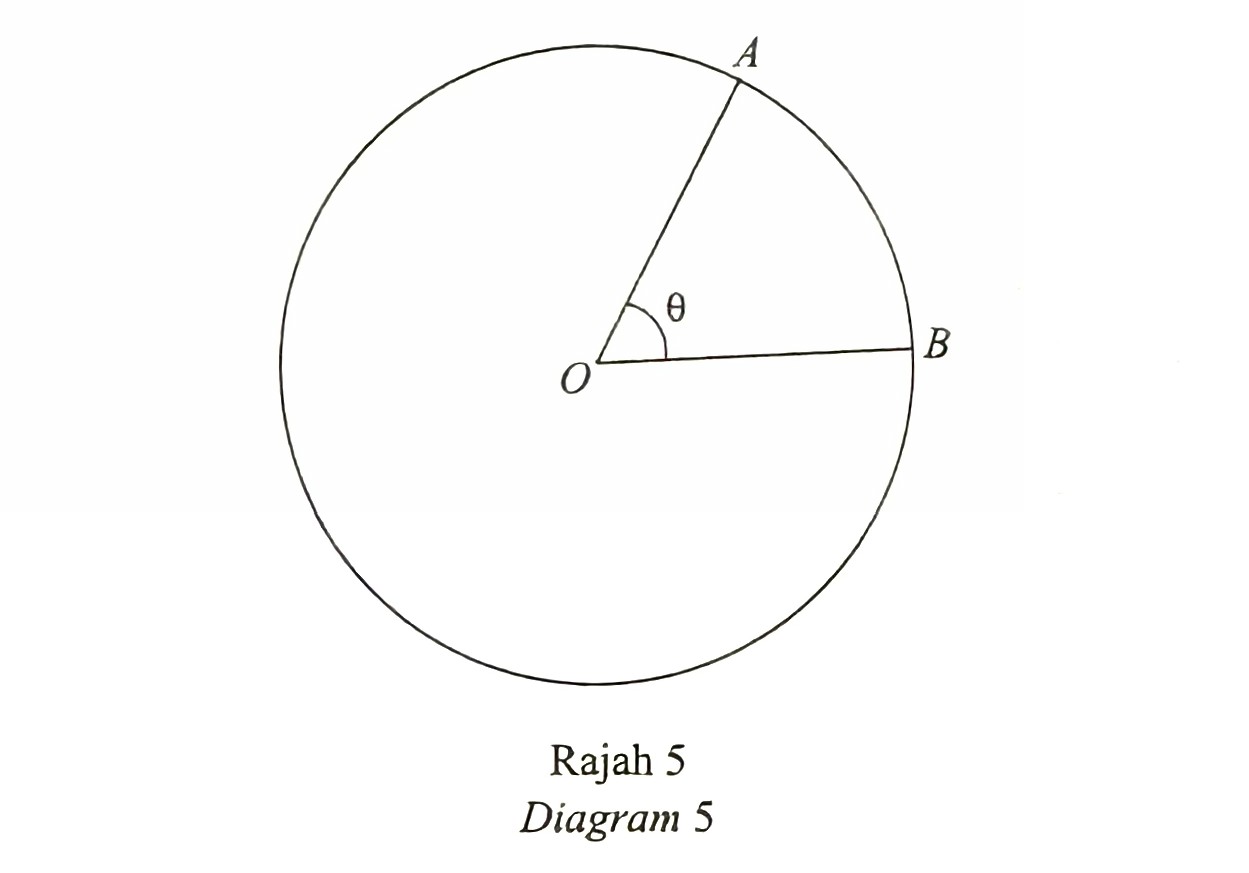
Berdasarkan Rajah 5, terbitkan s = jθ.
[2 markah]
Jawapan:
$$ \begin{aligned} \frac{\text { Panjang lengkok }}{\text { Lilitan bulatan }} & =\frac{\text { Sudut yang dicangkum di pusat }}{360^{\circ}} \\ \frac{s}{2 \pi j} & =\frac{\theta}{2 \pi} \\ s & =\frac{\theta}{2 \pi} \times 2 \pi j \\ s & =j \theta \end{aligned} $$
Rajah 5 menunjukkan sebuah bulatan dengan pusat O dan lengkok AB yang mencangkum sudut θ rad pada O. Diberi bahawa jejari bulatan itu ialah j unit dan panjang lengkok minor AB ialah s unit.

Berdasarkan Rajah 5, terbitkan s = jθ.
[2 markah]
Jawapan:
$$ \begin{aligned} \frac{\text { Panjang lengkok }}{\text { Lilitan bulatan }} & =\frac{\text { Sudut yang dicangkum di pusat }}{360^{\circ}} \\ \frac{s}{2 \pi j} & =\frac{\theta}{2 \pi} \\ s & =\frac{\theta}{2 \pi} \times 2 \pi j \\ s & =j \theta \end{aligned} $$