Soalan 12:
Rajah 6.1 menunjukkan kadbod MFH berbentuk segi tiga.
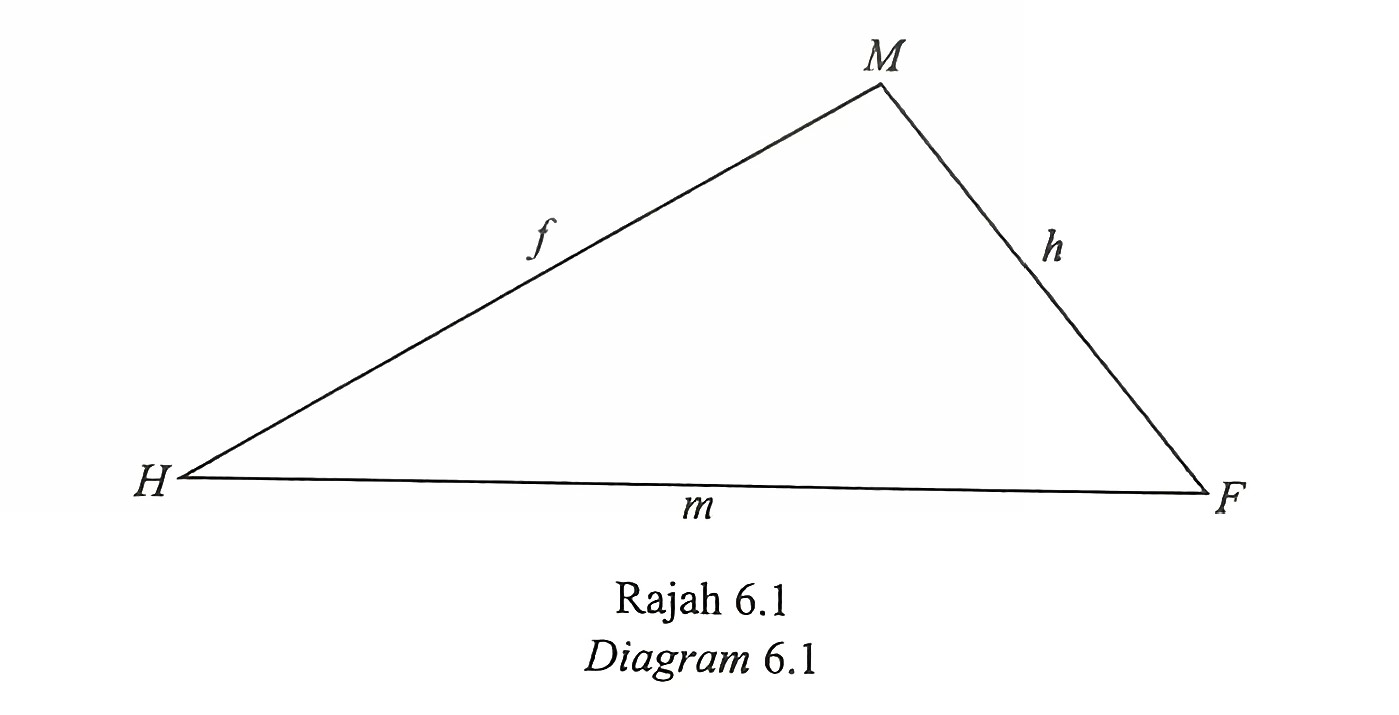
(a) Berdasarkan Rajah 6.1, terbitkan petua kosinus bagi sisi MH. [3 markah]
(b) Kadbod itu diletakkan ke dalam sebuah kuboid seperti yang ditunjukkan pada Rajah 6.2.
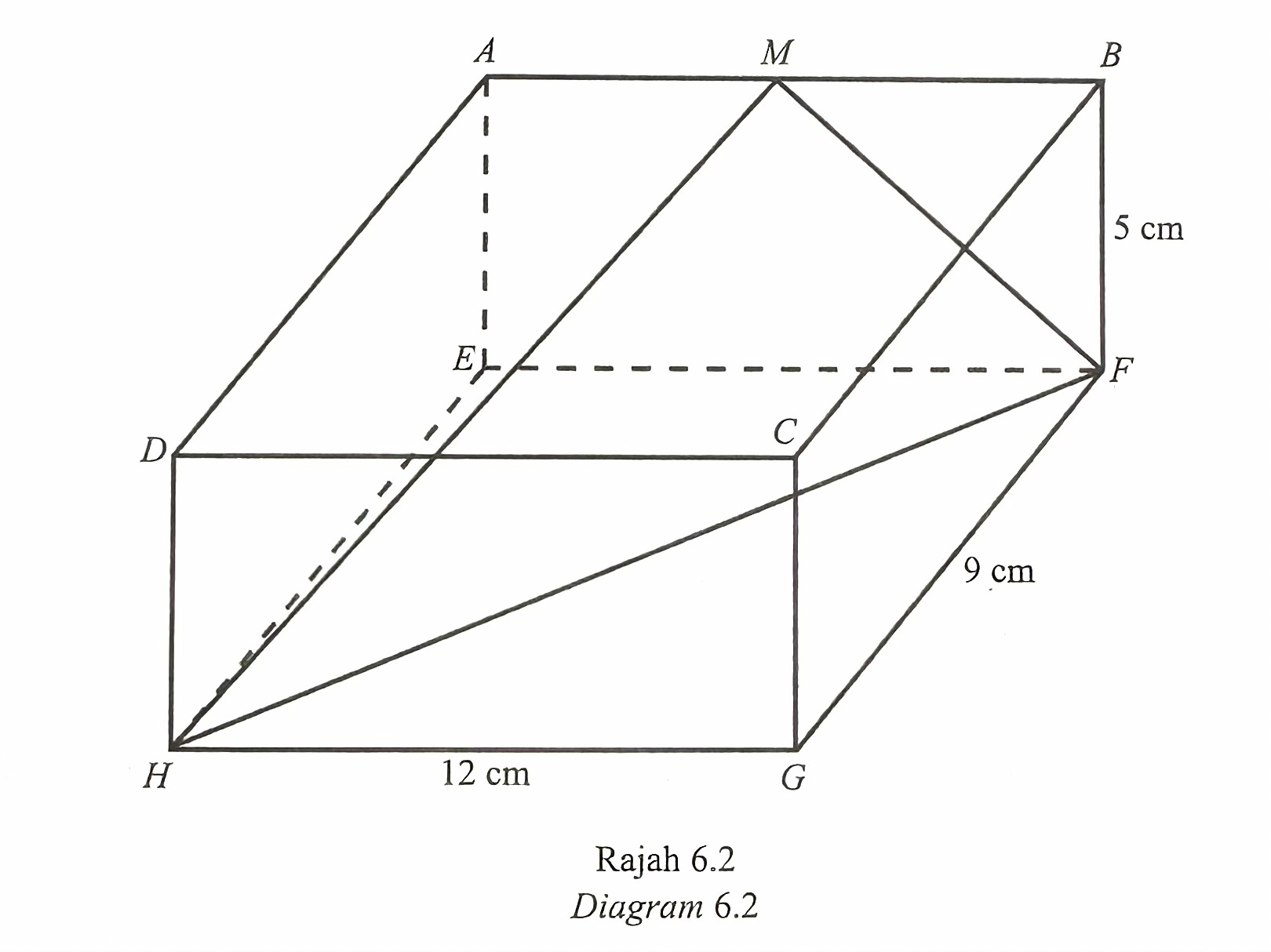
Diberi bahawa M ialah titik tengah bagi sisi AB.
(i) Cari ∠MFH.
(ii) Diberi bahawa ΔM’F’H’ mempunyai bentuk berbeza daripada ΔMFH dengan keadaan, M’F’ = MF, M’H’ = MH dan ∠M’H’F’ = ∠MHF.
(a) Lakar ΔM’F’H’
(b) Cari
Seterusnya, hitung luas, dalam cm2, of ΔM’F’H’.
[7 markah]
Jawapan:
(a)
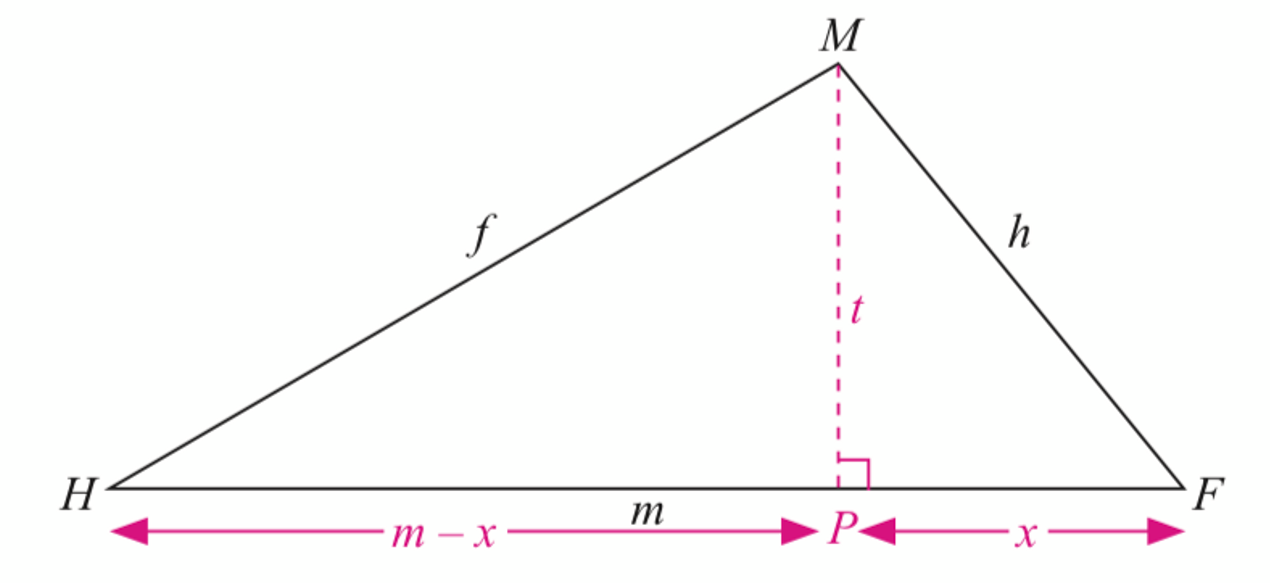
$$ \begin{aligned} &P F=x, P H=m-x, M P=t\\ &\text { Dengan Teorem Pythagoras, }\\ &\begin{aligned} & f^2=t^2+(m-x)^2 \\ & f^2=t^2+m^2-2 m x+x^2 \ldots (1) \end{aligned} \end{aligned} $$
$$ h^2=t^2+x^2 \ldots \text { (2) } $$
$$ \begin{aligned} & \mathrm{kos} \angle F=\frac{x}{h} \\ & x=h \mathrm{kos} \angle F \ldots (3) \end{aligned} $$
$$ \begin{aligned} &\text { (2) dan (3) } \rightarrow \text { (1); }\\ &\begin{aligned} & f^2=t^2+x^2+m^2-2 m x \\ & f^2=h^2+m^2-2 m(h \mathrm{kos} \angle F) \\ & f^2=h^2+m^2-2 m h \mathrm{kos} \angle F \end{aligned} \end{aligned} $$
(b)(i)
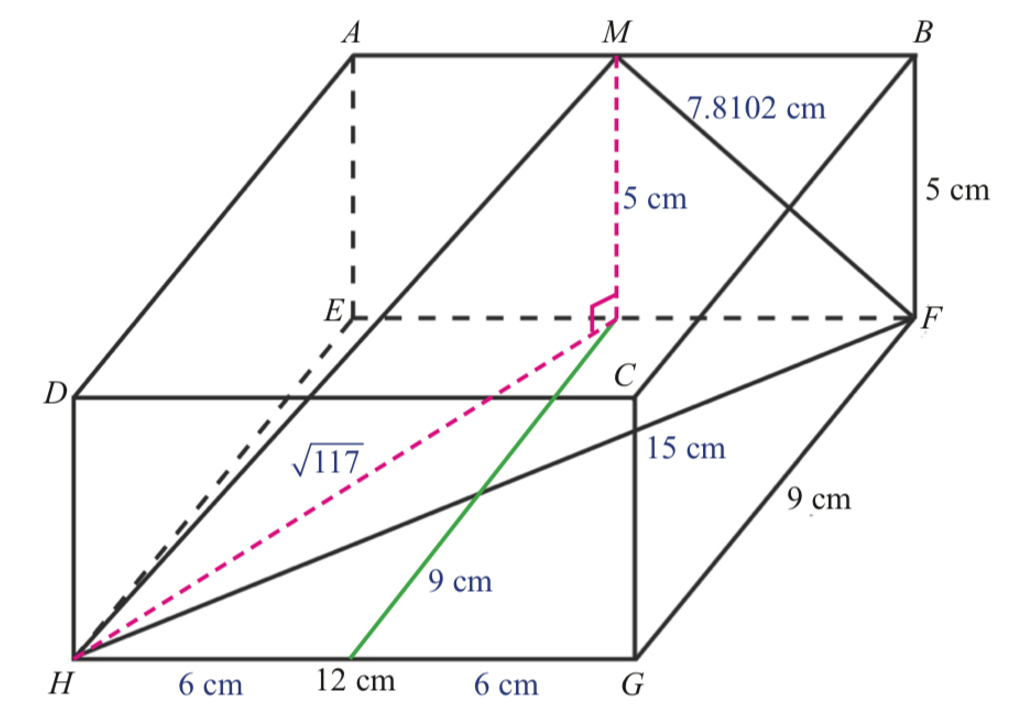
$$ \begin{aligned} & F M=\sqrt{6^2+5^2}=7.8102 \mathrm{~cm} \\ & F H=\sqrt{12^2+9^2}=15 \mathrm{~cm} \end{aligned} $$
$$ \begin{aligned} H C & =\sqrt{9^2+6^2} \\ & =\sqrt{117} \\ & =10.8167 \mathrm{~cm} \end{aligned} $$
$$ \begin{aligned} H M & =\sqrt{5^2+10.8167^2} \\ & =\sqrt{142} \\ & =11.9164 \mathrm{~cm} \end{aligned} $$
$$ \begin{aligned} H M^2= & M F^2+H F^2-2(M F)(H F) \\ & \text { kos } \angle M F H \\ (\sqrt{142})^2= & (7.8102)^2+(15)^2-2(7.8102)(15) \\ & \text { kos } \angle M F H \\ 142= & 285.9992-234.306 \mathrm{kos} \angle M F H \\ 234.306 \mathrm{kos} \angle M F H= & 285.9992-142 \\ 234.306 \mathrm{kos} \angle M F H= & 143.9992 \\ \angle M F H= & \mathrm{kos}^{-1} \left(\frac{143.9992}{234.306}\right) \\ \angle M F H= & \mathrm{kos}^{-1} (0.6146) \\ \angle M F H= & 52.08^{\circ} \end{aligned} $$
(b)(ii)(a)
$$ \begin{aligned} \angle F^{\prime} & =180^{\circ}-52.08^{\circ} \\ & =127.92^{\circ} \end{aligned} $$
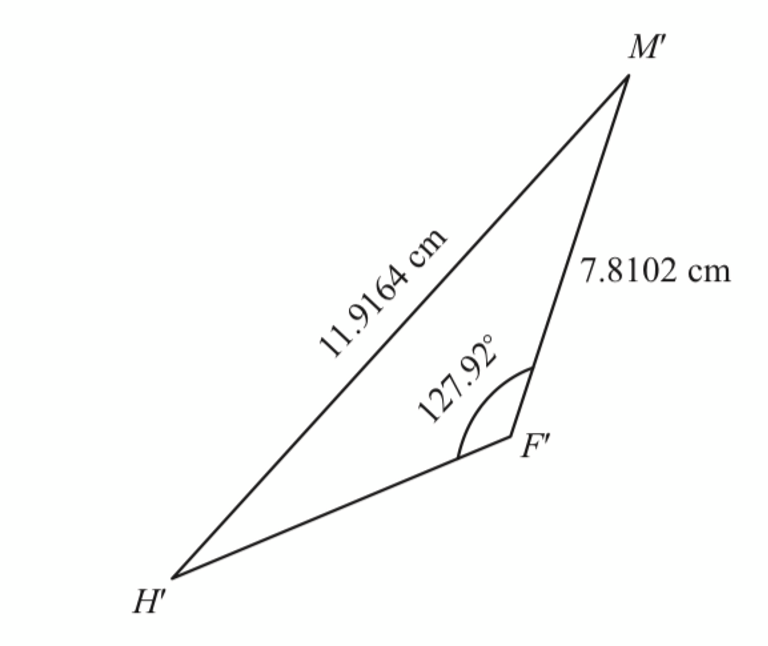
(b)(ii)(b)
$$ \begin{aligned} \frac{\sin \angle H}{7.8102} & =\frac{\sin 52.08^{\circ}}{11.9164} \\ \sin \angle H & =0.5170 \\ \angle H & =\sin ^{-1}(0.5170) \\ \angle H & =31.13^{\circ} \end{aligned} $$
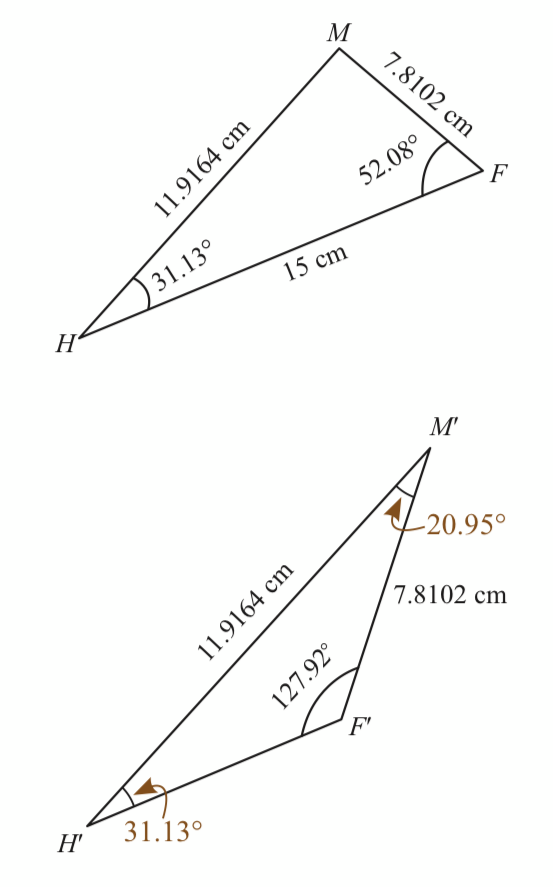
$$ \begin{aligned} \angle F^{\prime} M^{\prime} H^{\prime} & =180^{\circ}-31.13^{\circ}-127.92^{\circ} \\ & =20.95^{\circ} \end{aligned} $$
$$ \begin{aligned} \text { Luas } & =\frac{1}{2} a b \sin c \\ & =\frac{1}{2}(11.9164)(7.8102) \sin 20.95^{\circ} \\ & =16.6386 \mathrm{~cm}^2 \end{aligned} $$
Rajah 6.1 menunjukkan kadbod MFH berbentuk segi tiga.

(a) Berdasarkan Rajah 6.1, terbitkan petua kosinus bagi sisi MH. [3 markah]
(b) Kadbod itu diletakkan ke dalam sebuah kuboid seperti yang ditunjukkan pada Rajah 6.2.

Diberi bahawa M ialah titik tengah bagi sisi AB.
(i) Cari ∠MFH.
(ii) Diberi bahawa ΔM’F’H’ mempunyai bentuk berbeza daripada ΔMFH dengan keadaan, M’F’ = MF, M’H’ = MH dan ∠M’H’F’ = ∠MHF.
(a) Lakar ΔM’F’H’
(b) Cari
Seterusnya, hitung luas, dalam cm2, of ΔM’F’H’.
[7 markah]
Jawapan:
(a)

$$ \begin{aligned} &P F=x, P H=m-x, M P=t\\ &\text { Dengan Teorem Pythagoras, }\\ &\begin{aligned} & f^2=t^2+(m-x)^2 \\ & f^2=t^2+m^2-2 m x+x^2 \ldots (1) \end{aligned} \end{aligned} $$
$$ h^2=t^2+x^2 \ldots \text { (2) } $$
$$ \begin{aligned} & \mathrm{kos} \angle F=\frac{x}{h} \\ & x=h \mathrm{kos} \angle F \ldots (3) \end{aligned} $$
$$ \begin{aligned} &\text { (2) dan (3) } \rightarrow \text { (1); }\\ &\begin{aligned} & f^2=t^2+x^2+m^2-2 m x \\ & f^2=h^2+m^2-2 m(h \mathrm{kos} \angle F) \\ & f^2=h^2+m^2-2 m h \mathrm{kos} \angle F \end{aligned} \end{aligned} $$
(b)(i)

$$ \begin{aligned} & F M=\sqrt{6^2+5^2}=7.8102 \mathrm{~cm} \\ & F H=\sqrt{12^2+9^2}=15 \mathrm{~cm} \end{aligned} $$
$$ \begin{aligned} H C & =\sqrt{9^2+6^2} \\ & =\sqrt{117} \\ & =10.8167 \mathrm{~cm} \end{aligned} $$
$$ \begin{aligned} H M & =\sqrt{5^2+10.8167^2} \\ & =\sqrt{142} \\ & =11.9164 \mathrm{~cm} \end{aligned} $$
$$ \begin{aligned} H M^2= & M F^2+H F^2-2(M F)(H F) \\ & \text { kos } \angle M F H \\ (\sqrt{142})^2= & (7.8102)^2+(15)^2-2(7.8102)(15) \\ & \text { kos } \angle M F H \\ 142= & 285.9992-234.306 \mathrm{kos} \angle M F H \\ 234.306 \mathrm{kos} \angle M F H= & 285.9992-142 \\ 234.306 \mathrm{kos} \angle M F H= & 143.9992 \\ \angle M F H= & \mathrm{kos}^{-1} \left(\frac{143.9992}{234.306}\right) \\ \angle M F H= & \mathrm{kos}^{-1} (0.6146) \\ \angle M F H= & 52.08^{\circ} \end{aligned} $$
(b)(ii)(a)
$$ \begin{aligned} \angle F^{\prime} & =180^{\circ}-52.08^{\circ} \\ & =127.92^{\circ} \end{aligned} $$

(b)(ii)(b)
$$ \begin{aligned} \frac{\sin \angle H}{7.8102} & =\frac{\sin 52.08^{\circ}}{11.9164} \\ \sin \angle H & =0.5170 \\ \angle H & =\sin ^{-1}(0.5170) \\ \angle H & =31.13^{\circ} \end{aligned} $$

$$ \begin{aligned} \angle F^{\prime} M^{\prime} H^{\prime} & =180^{\circ}-31.13^{\circ}-127.92^{\circ} \\ & =20.95^{\circ} \end{aligned} $$
$$ \begin{aligned} \text { Luas } & =\frac{1}{2} a b \sin c \\ & =\frac{1}{2}(11.9164)(7.8102) \sin 20.95^{\circ} \\ & =16.6386 \mathrm{~cm}^2 \end{aligned} $$