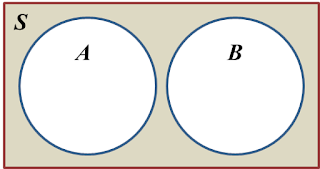
7.3 Kebarangkalian Peristiwa Saling Eksklusif


7.3  Kebarangkalian Peristiwa Saling Eksklusif
1. Peristiwa saling eksklusif ialah peristiwa-peristiwa yang tidak mungkin berlaku serentak.


2. Jika A dan B ialah dua peristiwa saling eksklusif,

P (A υ B) = P (A) + P (B)


Contoh:
Sebuah beg mengandungi 3 keping kad biru, 4 kad hijau dan 5 keping kad kuning. Sekeping kad dipilih secara rawak daripada beg itu. Cari kebarangkalian bahawa kad yang terpilih adalah berwarna hijau atau kuning.

Penyelesaian:
Katakan H = peristiwa sekeping kad hijau dipilih.
  K = peristiwa sekeping kad kuning dipilih.
Ruang sampel, S = 12, n (S) = 12
n (H) = 4 dan n (K) = 5
P(H)= n( H ) n( S ) = 4 12 P(K)= n( K ) n( S ) = 5 12

Peristiwa H dan K tidak dapat berlaku serentak kerana kita tidak mungkin memilih kad hijau dan kad kuning pada masa yang sama. Oleh itu, peristiwa H dan K adalah saling eksklusif.
H ∩ K = ∅ P ( H ∪ K ) = P ( H ) + P ( K ) = 4 12 + 5 12 = 9 12 = 3 4


Leave a Comment