Soalan 6:
Rajah di bawah menunjukkan semi bulatan PTQ, dengan pusat O dan sukuan RST, dengan pusat R.

Penyelesaian:
Rajah di bawah menunjukkan semi bulatan PTQ, dengan pusat O dan sukuan RST, dengan pusat R.

Hitung
(a) nilai θ, dalam radian,
(b) perimeter, dalam cm, seluruh rajah itu,
(c) luas, dalam cm2, kawasan berlorek itu.
Penyelesaian:
Soalan 7:
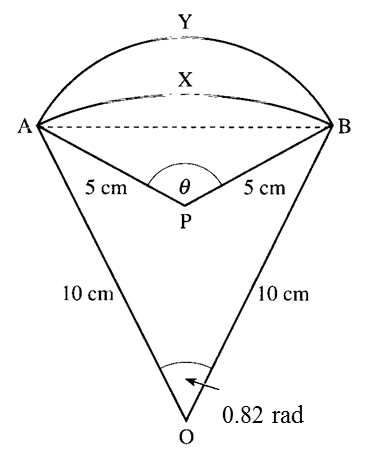
Dalam rajah di atas, AXB ialah lengkok sebuah bulatan berpusat O dan jejari 10cm dengan ∠AOB = 0.82 radian. AYB ialah lengkok sebuah bulatan berpusat P dan jejari 5cm dengan ∠APB = θ. Hitung:
(a) Panjang perentas AB,
(b) nilai θ dalam radian,
(c) Perbezaan panjang antara lengkok AYB dan lengkok AXB.
Penyelesaian:
(a)
½ AB = sin 0.41 × 10 (tukar mode kalkulator kepada Rad)
½ AB = 3.99
Maka panjang perentas AB = 3.99 × 2 = 7.98cm.
(b)
Katakan ½θ = α, θ = 2α
α = 0.924 rad
Maka θ = 0.924 × 2 = 1.848 rad
(c)
Guna s = jθ
Lengkok AXB = 10 × 0.82 = 8.2 cm
Lengkok AYB = 5 × 1.848 = 9.24 cm
Perbezaan panjang antara lengkok AYB dan lengkok AXB
= 9.24 – 8.2
= 1.04 cm
Soalan 8:
Rajah di bawah menunjukkan bulatan PQT yang berpusat O dan berjejari 7 cm.

QS ialah garis tangen kepada bulatan pada titik Q dan QSR adalah sukuan bagi bulatan berpusat Q. Q ialah titik tengah bagi OR dan QP adalah garis perentas. OQR dan SOP adalah garis lurus.
[Guna π = 3.142]
Hitung
(a) sudut θ, dalam radian,
(b) perimeter, dalam cm, bagi kawasan berlorek,
(c) luas, dalam cm2, bagi kawasan berlorek.
Penyelesaian:
(a)
(b)
(c)
Rajah di bawah menunjukkan bulatan PQT yang berpusat O dan berjejari 7 cm.

QS ialah garis tangen kepada bulatan pada titik Q dan QSR adalah sukuan bagi bulatan berpusat Q. Q ialah titik tengah bagi OR dan QP adalah garis perentas. OQR dan SOP adalah garis lurus.
[Guna π = 3.142]
Hitung
(a) sudut θ, dalam radian,
(b) perimeter, dalam cm, bagi kawasan berlorek,
(c) luas, dalam cm2, bagi kawasan berlorek.
Penyelesaian:
(a)
(b)
(c)
Soalan 9 (SPM 2017 – 8 markah):
Rajah 1 menunjukkan bulatan dan sektor sebuah bulatan dengan pusat sepunya O. Jejari bulatan ialah r cm.
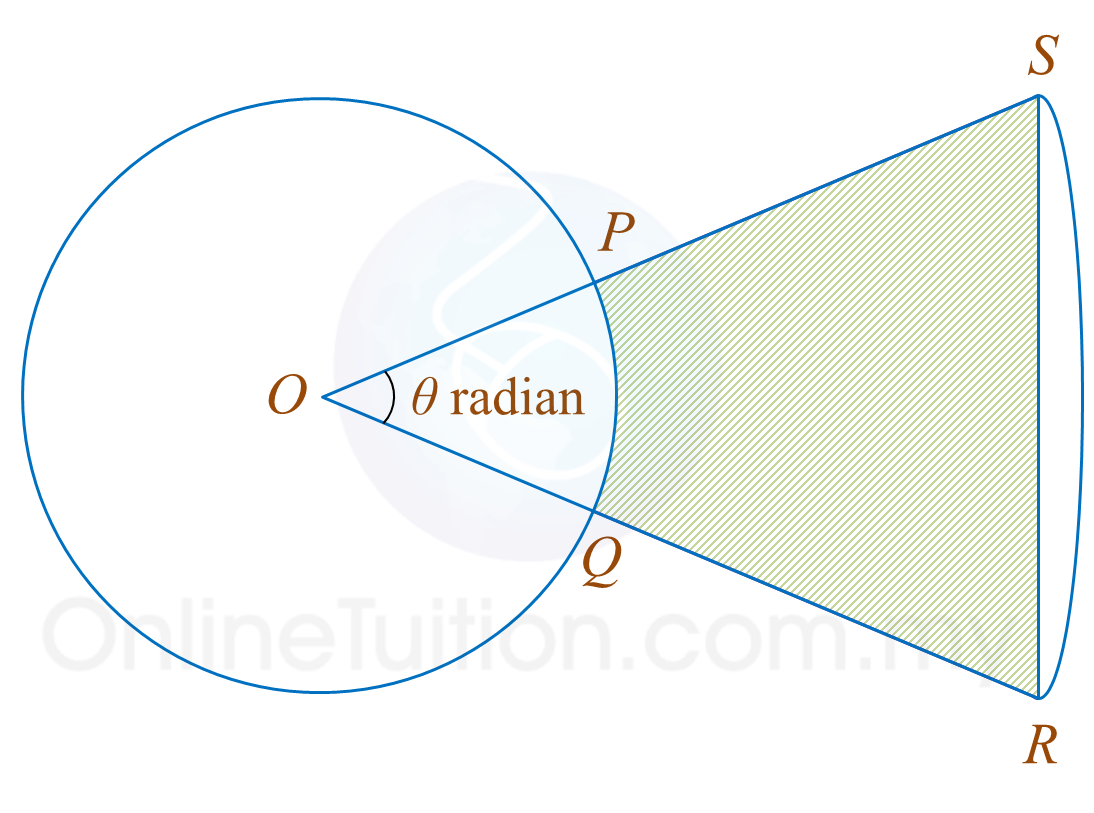
Diberi bahawa panjang lengkok PQ dan lengkok RS masing-masing ialah 2 cm dan 7 cm. QR = 10 cm.
[Guna θ = 3.142]
Cari
(a) nilai r dan nilai θ,
(b) luas, dalam cm2, kawasan yang berlorek.
Rajah 1 menunjukkan bulatan dan sektor sebuah bulatan dengan pusat sepunya O. Jejari bulatan ialah r cm.

Diberi bahawa panjang lengkok PQ dan lengkok RS masing-masing ialah 2 cm dan 7 cm. QR = 10 cm.
[Guna θ = 3.142]
Cari
(a) nilai r dan nilai θ,
(b) luas, dalam cm2, kawasan yang berlorek.
Penyelesaian:
(a)
(b)
Soalan 10 (SPM 2018 – 7 markah):
Persatuan matematik SMK Mulia menganjurkan satu pertandingan mencipta logo untuk persatuan itu.
Rajah 3 menunjukkan logo berbentuk bulatan yang dicipta oleh Adrian. Ketiga-tiga kawasan berwarna biru adalah kongruen. Diberi bahawa perimeter bagi kawasan berwarna biru ialah 20π cm.
[Guna π = 3.142]
Cari
(a) jejari, dalam cm, bagi logo itu kepada integer terhampir,
(b) luas, dalam cm2, bagi kawasan yang berwarna kuning.
Penyelesaian:
(a)
(b)

Persatuan matematik SMK Mulia menganjurkan satu pertandingan mencipta logo untuk persatuan itu.

Rajah 3 menunjukkan logo berbentuk bulatan yang dicipta oleh Adrian. Ketiga-tiga kawasan berwarna biru adalah kongruen. Diberi bahawa perimeter bagi kawasan berwarna biru ialah 20π cm.
[Guna π = 3.142]
Cari
(a) jejari, dalam cm, bagi logo itu kepada integer terhampir,
(b) luas, dalam cm2, bagi kawasan yang berwarna kuning.
Penyelesaian:
(a)
(b)
