1.5.1 Sukatan Membulat, SPM Praktis (Kertas 2)
Soalan 1:
Rajah menunjukkan sebuah bulatan berpusat O dan berjejari 8 cm terterap dalam sektor SPT bagi sebuah bulatan berpusat P. Garis lurus SP dan garis lurus TP adalah tangen kepada bulatan masing-masing di titik Q dan titik R.
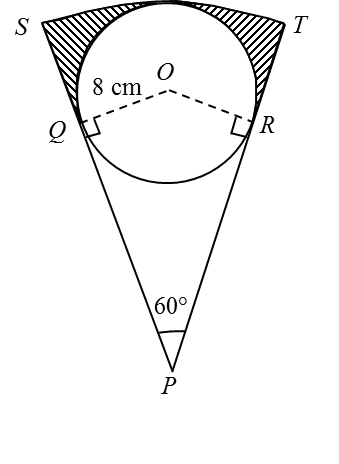
[Guna π = 3.142]
Hitung
(a) panjang, dalam cm, lengkok ST,
(b) luas, dalam cm2, kawasan berlorek.
Penyelesaian:
(a)
Bagi segitiga OPQ,
Jejari bagi sektor SPT = 16 + 8 = 24 cm
Panjang lengkok ST = 24 × 1.047 = 25.14 cm
(b)
Bagi segitiga OPQ,
∠QOR = 2(60o) = 120o
Sudut refleks ∠QOR = 360o – 120o = 240o
Luas kawasan berlorek
= (Luas sektor SPT) – (Luas sector major OQR) – (Luas ∆ OPQ dan ∆ OPR)
= ½ (24)2 (1.047) – ½ (8)2 (4.189) – 2 (½ × 8 × 13.86)
= 301.54 – 134.05 – 110.88
= 56.61 cm2
Soalan 2:
Rajah di bawah menunjukkan bulatan PQRT, berpusat Odan jejari 5 cm. AQB ialah tangen kepada bulatan itu di Q. Garis lurus, AO dan BO, bersilang dengan bulatan itu masing-masing di P dan R. OPQR ialah sebuah rombus. ACB ialah lengkok sebuah bulatan berpusat O.
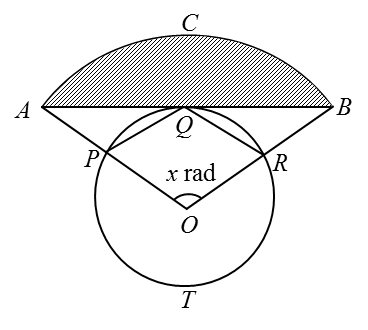

Hitungkan
(a) sudut x , dalam sebutan π,
(b) panjang, dalam cm , lengkok ACB,
(c) luas, dalam cm2, kawasan berlorek.
Penyelesaian:
(a)
Rombus ada 4 sisi sama, maka OP = PQ = QR = OR = 5 cm
OR ialah jejari kepada bulatan, maka OR = OQ = 5 cm
Segitiga OQR dan segitiga OPQ adalah segitiga sisi sama,
Maka, ∠ QOR = ∠QOP = 60o
∠ POR = 120o
(b)
Panjang lengkok, ACB,
s = jθ
Panjang ACB = (10) (2π / 3)
Panjang ACB = 20.94 cm
(c)
Luas kawasan berlorek
= ½ j2 (θ – sinθ) (tukar mode kalkulator kepada Rad)
= 50 (2.094 – 0.866)
= 61.40 cm2