2.8.1 Pembezaan, SPM Praktis (Kertas 2 Soalan 1 - 5)

Soalan 1:

Lengkung y = x³ – 6x² + 9x + 3 melalui titik P (2, 5) dan mempunyai dua titik pusingan A (3, 3) dan B.

Cari

(a) kecerunan lengkung itu pada P.

(b) persamaan normal kepada lengkung itu pada P.

Penyelesaian:

(a)

y = x³ – 6x² + 9x + 3

dy/dx = 3x² – 12x + 9

di titik P (2, 5),

dy/dx = 3(2)² – 12(2) + 9 = –3

Kecerunan lengung pada titik P = –3.

(b)

Kecerunan normal pada titik P = ⅓

persamaan normal pada P (2, 5):

y – y₁= m (x – x₁)

y – 5 = ⅓ (x– 2)

3y – 15 = x – 2

3y = x + 13

(c)

Pada titik pusingan dy/dx= 0.

3x² – 12x + 9 = 0

x² – 4x + 3 = 0

(x – 1)( x – 3) = 0

x – 1 = 0 atau x – 3 = 0

x = 1 atau x = 3 (titik A)

Pada titik B:

x = 1

y = (1)³– 6(1)² + 9(1) + 3 = 7

Maka, koordinat B = (1, 7)

\begin{array}{l} Apabila x = 1, \\ \frac{d^{2} y}{d x^{2}} = 6 x - 12 \\ \frac{d^{2} y}{d x^{2}} = 6 (1) - 12 \\ \frac{d^{2} y}{d x^{2}} = - 6 < 0 \\ \frac{d^{2} y}{d x^{2}} < 0, B ialah titik maksimum . \end{array}

Soalan 2:

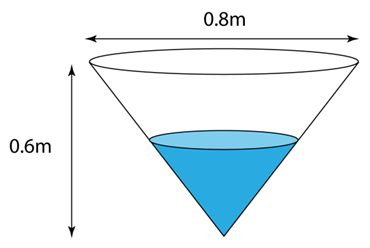
Rajah di atas menunjukkan sebuah kon dengan diameter 0.8m dan tinggi 0.6m. Air dituang ke dalam kon dengan kadar tetap 0.02m³s^-1. Cari kadar perubahan tinggi paras air pada ketika tinggi parasnya ialah 0.5m.

Penyelesaian:

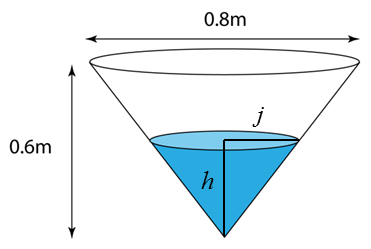
\begin{array}{l} Isipadu air, I = \frac{1}{3} π j^{2} h \\ I = \frac{1}{3} π {(\frac{2}{3} h)}^{2} h \\ I = \frac{4}{27} π h^{3} \\ \frac{d I}{d h} = (3) \frac{4}{27} π h^{2} \\ \frac{d I}{d h} = \frac{4}{9} π h^{2} \end{array}

Kadar perubahan tinggi paras air pada ketika tinggi parasnya ialah 0.5m =

\frac{d h}{d t} .

\begin{array}{l} \frac{d h}{d t} = \frac{d h}{d I} \times \frac{d I}{d t} \leftarrow Petua rantai \\ \frac{d h}{d t} = \frac{9}{4 π h^{2}} \times 0.02 \leftarrow Diberi \frac{d I}{d t} = 0.02 \\ \frac{d h}{d t} = \frac{9}{4 π {(0.5)}^{2}} \times 0.02 \\ \frac{d h}{d t} = 0.0572 m s^{- 1} \end{array}

Katakan,

h = tinggi paras air

j = jejari permukaan air

I = isipadu air

\begin{array}{l} \frac{j}{h} = \frac{0.4}{0.6} \leftarrow Konsep segitiga serupa \\ \frac{j}{h} = \frac{2}{3} \\ j = \frac{2}{3} h \end{array}

Soalan 3:

(a) Seorang pekerja di kedai mainan kanak-kanak sedang mengisi udara ke dalam sebuah belon yang berbentuk sfera dengan kadar 25 cm³ s^-1. Dengan meninggalkan jawapan dalam sebutan π.

[Isipadu sfera, V = \frac{4}{3} π j^{3}]

Cari,
(i) kadar perubahan jejari belon itu pada ketika jejarinya 10 cm. [3 markah]
(ii) Perubahan hampir bagi isipadu apabila jejari belon mneyusut dari 10cm kepada 9.95cm. [2 markah]

(b) Lengkung

y = h x^{3} - \frac{3}{x}

mempunyai titik pusingan x = 1, cari nilai h. [3 markah]

Penyelesaian:

(a)(i)

\begin{array}{l} V = \frac{4}{3} π j^{3} \\ \frac{d V}{d j} = 4 π j^{2} \\ \frac{d j}{d t} = \frac{d j}{d V} \times \frac{d V}{d t} \\ = \frac{1}{4 π j^{2}} \times 25 \\ = \frac{1}{4 π {(10)}^{2}} \times 25 \\ = \frac{1}{16 π} \end{array}

(a)(ii)

\begin{array}{l} \frac{δ V}{δ j} \approx \frac{d V}{d j} \\ δ V = \frac{d V}{d j} \times δ j \\ = 4 π j^{2} \times (9.95 - 10) \\ = 4 π {(10)}^{2} \times (- 0.05) \\ = - 20 π \end{array}

(b)

\begin{array}{l} y = h x^{3} - \frac{3}{x} \\ y = h x^{3} - 3 x^{- 1} \\ \frac{d y}{d x} = 3 h x^{2} + 3 x^{- 2} \\ \frac{d y}{d x} = 3 h x^{2} + \frac{3}{x^{2}} \\ Pada titik pusingan, \frac{d y}{d x} = 0 \\ 0 = 3 h x^{2} + \frac{3}{x^{2}} \\ 0 = 3 h {(1)}^{2} + \frac{3}{1} \to diberi x = 1 \\ 3 h = - 3 \\ h = - 1 \end{array}

Soalan 4 (SPM 2017 - 7 markah):
Diberi bahawa persamaan suatu lengkung ialah

y = \frac{5}{x^{2}} .

(a) Cari nilai

\frac{d y}{d x}

apabila x = 3.
(b) Seterusnya, anggarkan nilai bagi

\frac{5}{{(2.98)}^{2}} .

Penyelesaian:
(a)

\begin{array}{l} y = \frac{5}{x^{2}} = 5 x^{- 2} \\ \frac{d y}{d x} = - 10 x^{- 3} \\ = - \frac{10}{x^{3}} \\ Apabila x = 3 \\ \frac{d y}{d x} = - \frac{10}{3^{3}} = - \frac{10}{27} \end{array}

(b)

\begin{array}{l} δ x = 2.98 - 3 = - 0.02 \\ δ y = \frac{d y}{d x} . δ x \\ = - \frac{10}{27} \times (- 0.02) \\ = 0.007407 \\ Nilai bagi \frac{5}{{(2.98)}^{2}} \\ = y + δ y \\ = \frac{5}{x^{2}} + (0.007407) \\ = \frac{5}{3^{2}} + (0.007407) \\ = 0.56296 \end{array}

Soalan 5 (SPM 2018 - 6 markah):
Rajah 4 menunjukkan pandangan hadapan sebahagian daripada laluan ‘roller coaster’ di sebuah taman replika.

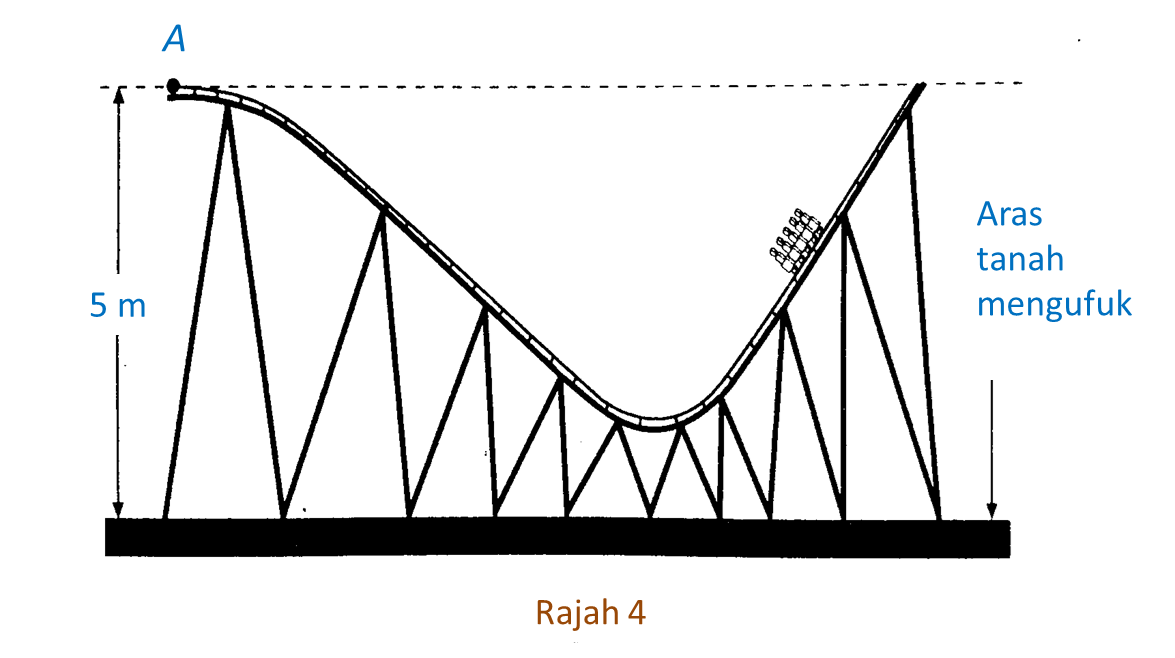
Bahagian lengkung laluan ‘roller coaster’ itu diwakili oleh persamaan

y = \frac{1}{64} x^{3} - \frac{3}{16} x^{2}

, dengan titik A sebagai asalan.
Cari jarak tegak terpendek, dalam m, dari laluan itu ke aras tanah.

Penyelesaian:

\begin{array}{l} y = \frac{1}{64} x^{3} - \frac{3}{16} x^{2} ............... (1) \\ \frac{d y}{d x} = 3 (\frac{1}{64}) x^{2} - 2 (\frac{3}{16}) x^{1} \\ = \frac{3}{64} x^{2} - \frac{3}{8} x \\ Pada titik pusingan, \frac{d y}{d x} = 0 \\ \frac{3}{64} x^{2} - \frac{3}{8} x = 0 \\ x (\frac{3}{64} x - \frac{3}{8}) = 0 \\ x = 0 atau \\ \frac{3}{64} x - \frac{3}{8} = 0 \\ \frac{3}{64} x = \frac{3}{8} \\ x = \frac{3}{8} \times \frac{64}{3} \\ x = 8 \end{array}

$\begin{array}{l} Gantikan nilai-nilai x ke dalam (1): \\ Apabila x = 0, \\ y = \frac{1}{64} {(0)}^{3} - \frac{3}{16} {(0)}^{2} \\ y = 0 \\ Apabila x = 8, \\ y = \frac{1}{64} {(8)}^{3} - \frac{3}{16} {(8)}^{2} \\ y = - 4 \\ Oleh itu, titik-titik pusingan : (0, 0) dan (8, - 4) \end{array}$

\begin{array}{l} \frac{d y}{d x} = \frac{3}{64} x^{2} - \frac{3}{8} x \\ \frac{d^{2} y}{d x^{2}} = 2 (\frac{3}{64}) x - \frac{3}{8} \\ = \frac{3}{32} x - \frac{3}{8} \\ Apabila x = 0, \\ \frac{d^{2} y}{d x^{2}} = \frac{3}{32} (0) - \frac{3}{8} \\ = - \frac{3}{8} (< 0) \\ (0, 0) ialah titik maksimum . \end{array}

\begin{array}{l} Apabila x = 8, \\ \frac{d^{2} y}{d x^{2}} = \frac{3}{32} (8) - \frac{3}{8} \\ = \frac{3}{8} (> 0) \\ (8, - 4) ialah titik minimum . \\ Jarak tegak terpendek dari laluan ke aras tanah \\ adalah pada titik minimum . \\ Jarak tegak terpendek \\ = 5 - 4 \\ = 1 m \end{array}

1 thought on “2.8.1 Pembezaan, SPM Praktis (Kertas 2 Soalan 1 – 5)”

Merdecka Walesr

October 4, 2018 at 11:23 pm | Reply

Cikgu,begitu sedikit soalan kbat ni,boleh cikgu mempertambahkan lagi soalan soalan spm dari tahun leaps yang melibatkan kemahiran berfikir aras tinggi,Saya berharap cikgu akan membanfu saya dalam menjalani peperiksaan sijil pelajaran malaysia SPN pada tahun hadapan,,, 🙂

1 thought on “2.8.1 Pembezaan, SPM Praktis (Kertas 2 Soalan 1 – 5)”

Leave a Comment Cancel reply