Matematik Tambahan SPM 2018, Kertas 1 (Soalan 1 – 4)

Soalan 1 (2 markah):
Rajah 1 menunjukkan graf taburan kebarangkalian bagi suatu pemboleh ubah rawak X, X ~ N(μ, σ²).

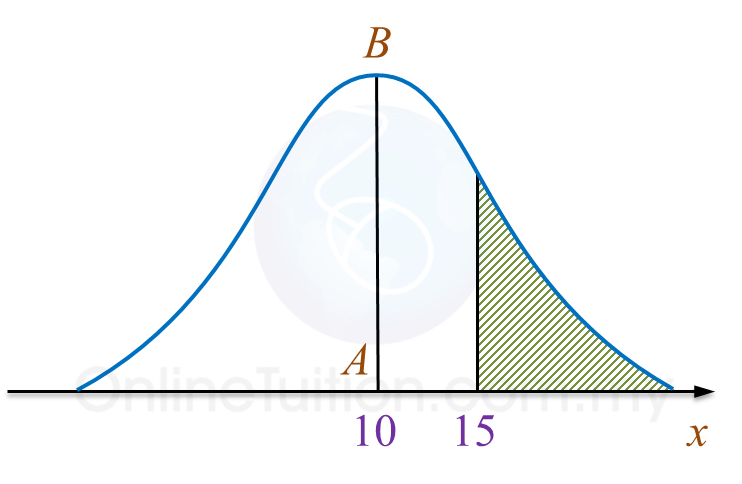Rajah 1

Diberi bahawa AB adalah paksi simetri bagi graf itu.
(a) Nyatakan nilai μ.
(b) Jika luas kawasan berlorek ialah 0.38, nyatakan nilai bagi P(5 ≤ X ≤ 15).

Penyelesaian:
(a)
μ = 0

(b)
P(10 ≤ X ≤ 15)
= 0.5 – 0.38
= 0.12

P(5 ≤ X ≤ 10)
= P(10 ≤ X ≤ 15)
= 0.12

Maka P(5 ≤ X ≤ 15)
= 0.12 + 0.12
= 0.24

Soalan 2 (2 markah):
$\begin{array}{l}\left(\text{a}\right)\text{ Diberi }{}^{6}C{}_n>1\text{, senaraikan semua}\\ \text{nilai-nilai yang mungkin bagi }n\text{.}\\ \left(\text{b}\right)\text{ Diberi }{}^{y}C{}_m={}^{y}C{}_n\text{, ungkapkan }y\\ \text{dalam sebutan }m\text{ dan }n\text{.}\end{array}$

Penyelesaian:
(a)
n = 1, 2, 3, 4, 5

(b)
y = m + n

Soalan 3 (2 markah):
Jadual 1 menunjukkan maklumat tentang suatu set data.

Jadual 1

Nyatakan
(a) nilai p jika m = 20,
(b) nilai q jika p = 2.5.


Penyelesaian:
(a)
Sisihan piawai baharu = sisihan piawai asal × p
20 = 5 × p
p = 4

(b)
Median baharu = [median asal × p] + 1
q = 2p × 1
q = 2(2.5) + 1
q = 5 + 1
q = 6

Soalan 4 (3 markah):
Jadual 2 menunjukkan taburan skor yang diperolehi sekumpulan murid dalam suatu pertandingan.

Jadual 2

(a) Nyatakan nilai minimum bagi x jika skor mod ialah 4.
(b) Cari min skor bagi taburan itu jika x = 1.

 
Penyelesaian:
(a)
Nilai minimum bagi x = 8

(b)
$\begin{array}{l}\text{Min}\\ =\frac{1\left(3\right)+2\left(6\right)+3\left(7\right)+4\left(1\right)+5\left(1\right)}{3+6+7+1+1}\\ =\frac{45}{18}\\ =2.5\end{array}$