6.2.1 Enam Fungsi Trigonometri bagi Sebarang Sudut
(A) Mentakrifkan Sinus, kosinus, tan, kosek, sek and kot
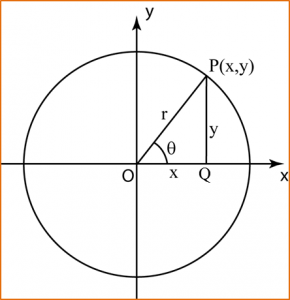

1. Katakan P (x, y) ialah sebarang sudut yang terletak pada lilitan bulatan yang berpusat O dan berjejari, j. Berdasarkan ∆ OPQ dalam rajah di atas,
\(\boxed{\begin{equation}
\sin \theta=\frac{y}{r} \cdot \operatorname{kos} \theta=\frac{x}{r} \cdot \tan \theta=\frac{y}{x}
\end{equation}}\)
2. Bagi sebarang sudut θ,
\(\boxed{\begin{array}{l}
\tan \theta=\frac{\sin \theta}{k o s \theta} \\
k o t \theta=\frac{1}{\tan \theta}=\frac{k o s \theta}{\sin \theta} \\
\operatorname{sek} \theta=\frac{1}{\operatorname{kos} \theta} \\
\operatorname{kosek} \theta=\frac{1}{\sin \theta}
\end{array}}\)
|
Sudut Pelengkap:
• sin θ = kos (90o – θ)
• kos θ = sin (90o – θ)
• tan θ = kot (90o – θ)
• kot θ = tan (90o – θ)
• sek θ = kosek (90o – θ)
• kosek θ = sek (90o – θ)
|
Misalnya,
(a) sin 75o= kos (90o – 75o) = kos 15o
(b) tan 50o= kot (90o – 50o) = kot 20o
(c) sek 25o= kosek (90o – 25o) = kosek 65o
|
Sudut Negatif:
• sin (–θ) = –sin θ
• kos (–θ) = kos θ
• tan (–θ) = –tanθ
|
· Sudut negatif ialah sudut yang diukur mengikut arah jam dari arah positif paksi-x.
· Misalnya, –60o adalah sepadan dengan 300o (360o – 60o).
Contoh:
Ungkapkan setiap fungsi trigonometri yang berikut dalam sebutan nisbah sudut tirus trigonometri.
Seterusnya, cari nilainya dengan menggunakan kalkulator.
(a) kos (– 325o)
(b) tan (– 124o)
(c) sin (– 115o)
(a) kos (– 325o)
= kos 325o ← {rumus kos (–θ) = kos θ digunakan}
= kos (360o– 325o) ← {kos bernilai positif di sukuan keempat}
= kos 35o
= 0.8192
(b) tan (– 124o)
= – tan 124o ← {rumus tan (–θ) = – tan θ digunakan }
= – [– tan (180o– 124o)] ← {tan bernilai negatif di sukuan kedua}
= tan 56o
= 1.483
(c) sin (– 115o)
= – sin 115o ← {rumus sin (–θ) = – sin θ digunakan }
= – sin (180o– 115o) ← {sin bernilai positif di sukuan kedua}
= – sin 65o
= – 0.9063