5.2.3 Kebarangkalian Sesuatu Peristiwa
(b)
Contoh:
Jisim epal dalam sebuah gerai adalah bertaburan normal dengan min 220g dan varians 100g. Cari kebarangkalian bahawa sebiji epal dipilih secara rawak mempunyai jisim
(a) lebih daripada 230g.
(b) di antara 210g dengan 225g.
Seterusnya, cari nilai h supaya 90% daripada epal mempunyai jisim lebih daripada h g.
Penyelesaian:
μ = 220g
σ = √100 = 10g
Katakan X ialah jisim buah epal.
(a)
P (X > 230)
\(=P{(Z>\frac{230-220}{10})}\leftarrow\boxed{\begin{array}{l}\text{Tukar kepada taburan normal}\\\text{piawai ~ rumus}Z=\frac{X-\mu}\sigma\end{array}}\)
= P (Z > 1)
= 0.1587
P (210 < X < 225)
\(=P{(\frac{210-220}{10}\;<\;Z\;<\;\frac{225-220}{10})}\leftarrow\boxed{\begin{array}{l}\text{Tukar kepada taburan}\\\text{normal piawai}\end{array}}\)
= P (–1 < Z < 0.5)
= 1 – P (Z > 1) – P (Z > 0.5)
= 1 – 0.1587 – 0.3085
= 0.5328
90% (kebarangkalian = 0.9) daripada epal mempunyai jisim lebih daripada h g,
P (X > h) = 0.9
P (X < h) = 1 – 0.9
= 0.1
Daripada sifir taburan normal piawai,
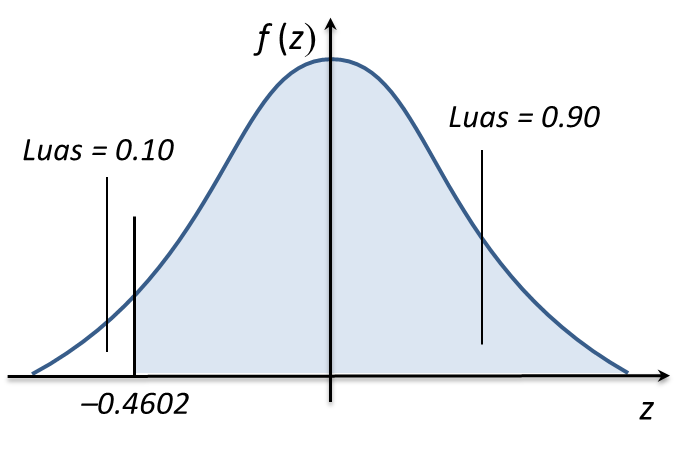
P (Z > 0.4602) = 0.1
P (Z < –0.4602) = 0.1
\(\frac{h-220}{10}=-0.4602\)
h – 220 = – 4.602
h = 215.4
