5.2 Taburan Normal
(A) Pembolehubah Rawak Selanjar
1. Pembolehubah rawak selanjar ialah suatu pembolehubah yang boleh mengambil sebarang nilai di dalam suatu selang.
(B) Taburan Normal
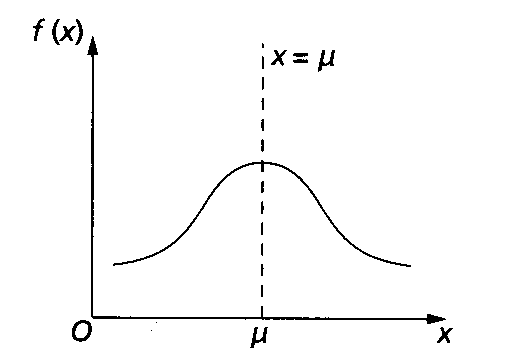
1. Suatu pembolehubah rawak selanjar, X, adalah bertaburan normal jika grafnya meunjukkan ciri-ciri berikut.

(a) Lengkungnya berbentuk loceng
(b) Ia bersimetri pada paksi tegak yang melalui minnya, iaitu line x = μ.
(c) Ia mempunyai nilai maximum di x = μ.
(d) Luas rantau yang dibatasi oleh lengkung dan paksi-x ialah 1, iaitu jumlah kebarangkalian bagi semua nilai X ialah 1.
2. Pembolehubah rawak selanjar, X, yang bertaburan normal ditulis sebagai X ~ N (µ, σ2) dengan m ialah min dan σ2 ialah varians.
(C) Taburan Normal Piawai
Jika suatu pembolehubah rawak normal, X, mempunyai min, µ = 0 dan sisihan piawai, σ = 1, maka X mengikut suatu taburan normal piawai, X ~ N (0, 1).
(D) Lengkung Suatu Taburan Normal Piawai
1. Lengkung bagi suatu taburan normal piawai mempunyai ciri-ciri yang berikut.
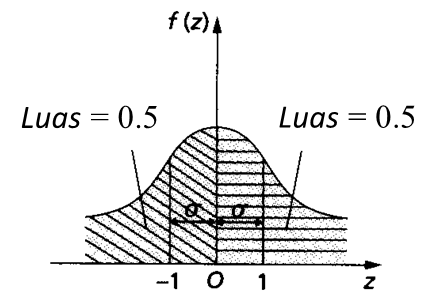
(a) Ia bersimetri pada paksi tegak yang melalui min, µ = 0 dan mempunyai varians, σ2 = 1.
(b) Ia mempunyai nilai maksimum pada Z = 0.
(c) Luas rantau yang dibatasi oleh lengkung taburan normal piawai dengan paksi-z ialah 1.
(E) Penukaran Pembolehubah Suatu Taburan Normal kepada Pembolehubah Taburan Normal Piawai
1. Suatu taburan normal boleh ditukar kepada taburan normal piawai dengan menggunakan:
\(\boxed{\text{ }Z=\frac{x-\mu}\sigma\text{ }}\)
dengan keadaan,
Z = skor piawai atau skor-z
X = nilai pembolehubah rawak normal
µ = min taburan normal
σ = sisihan piawai taburan normal