Soalan 3:
Jisim mangga di sebuah gerai mempunyai taburan normal dengan min 200g dan sisihan piawai 30g.
(a) Cari jisim, dalam g, sebiji mangga yang mempunyai skor-z bernilai 0.5.
(b) Jika sebiji mangga dipilih secara rawak, cari kebarangkalian bahawa mangga itu mempunyai jisim sekurang-kurangnya 194g.
Penyelesaian:
μ = 200g
σ = 30g
Katakan X ialah jisim sebiji mangga.
(a)
\(\frac{X-200}{30}=0.5\)
X = 0.5(30) + 200
X = 215g
(b)
P (X ≥ 194)
\(=P{(Z\geq\frac{194-200}{30})}\)
= P (Z ≥ –0.2)
= 1 – P (Z > 0.2)
= 1 – 0.4207
= 0.5793
Soalan 4:
Rajah di bawah menunjukkan satu graf taburan normal piawai.
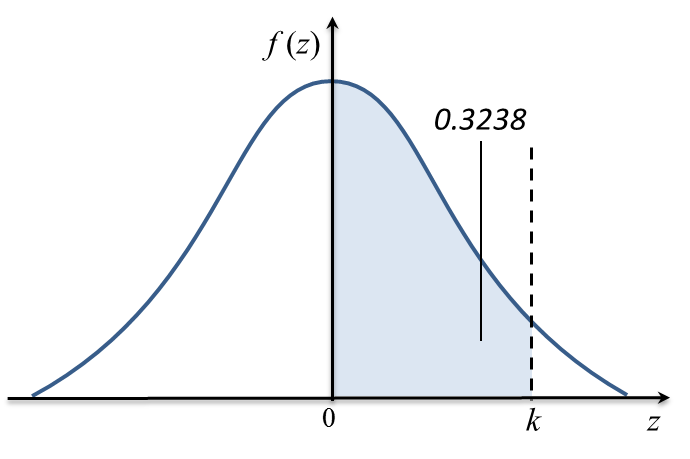Kebarangkalian yang diwakili oleh luas kawasan berlorek ialah 0.3238.(a) cari nilai k.
(b) X ialah pemboleh ubah rawak selanjar bertaburan secara normal dengan min 80 dan varians 9.
Cari nilai X apabila skor-z ialah k.
(a)
P (Z > k) = 0.5 – 0.3238
= 0.1762
k = 0.93
(b)
μ = 80,
σ2 = 9, σ = 3
\(\frac{X-80}3=0.93\)
X = 3 (0.93) + 80
X = 82.79