3.8.3 Pengamiran, SPM Praktis (Kertas 2)


Soalan 5
Dalam rajah di bawah, garis lurus WY ialah normal kepada lengkung y = 1 2 x 2 + 1  pada B (2, 4). Garis lurus BQ adalah selari dengan paksi-y.


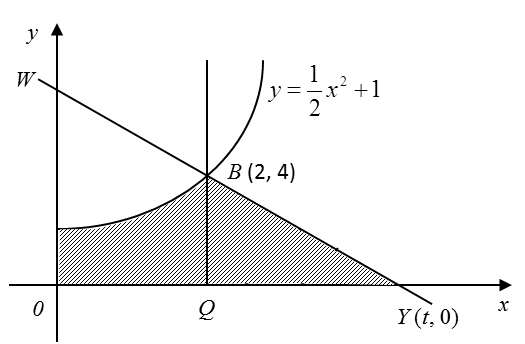
Cari
(a) nilai t,
(b) luas rantau yang berlorek,
(c) Isipadu janaan, dalam sebutan π, apabila rantau yang dibatasi oleh lengkung itu, paksi-y dan garis lurus y = 4 dikisarkan melalui 360o pada paksi-y.
Penyelesaian:
(a)
y= 1 2 x 2 +1 Kecerunan tangen,  dy dx =2( 1 2 x )=x pada titik B,  dy dx =2 Kecerunan normal,  m 2 =− 1 2 4−0 2−t =− 1 2 8=−2+t t=10  


(b)
Luas rantau yang berlorek
= Luas di bawah lengkung + Luas segi tiga BQY
= ∫ 0 2 ( 1 2 x 2 + 1 ) d x + 1 2 ( 10 − 2 ) ( 4 ) = [ x 3 6 + x ] 0 2 + 16 = [ 8 6 + 2 ] − 0 + 16 = 19 1 3 unit 2


(c)
Pada paksi-y, x = 0, y = ½ (0) + 1 = 1
y = 1 2 x 2 + 1 → x 2 = 2 y − 2 Isipadu janaan = π ∫ x 2 d y = π ∫ 1 4 ( 2 y − 2 ) d y = π [ y 2 − 2 y ] 1 4 = π [ ( 16 − 8 ) − ( 1 − 2 ) ] = 9 π unit 3



Soalan 6:
Rajah di bawah menunjukkan sebahagian daripada lengkung y = 2 ( 3 x − 2 ) 2  yang melalui B (1, 2).


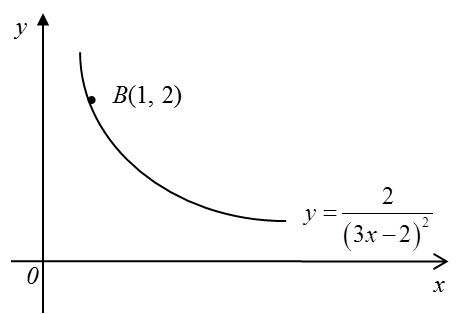
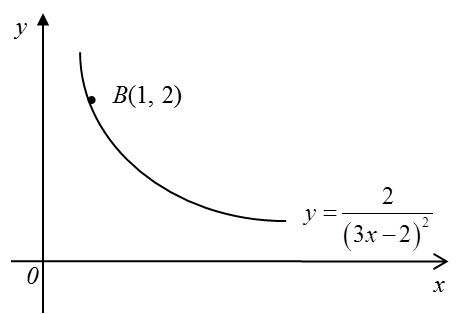
(a)   Carikan persamaan tangen kepada lengkung itu pada titik B.
(b)   Suatu rantau dibatasi oleh lengkung itu, paksi-x, garis lurus x = 2 dan x = 3.
(i) Cari luas rantau yang berlorek.
(ii) Rantau itu dikisarkan melalui 360o pada paksi-x.
Carikan isipadu janaan, dalam sebutan π.

Penyelesaian:
(a)
y = 2 ( 3 x − 2 ) 2 = 2 ( 3 x − 2 ) − 2 d y d x = − 4 ( 3 x − 2 ) − 3 ( 3 ) d y d x = − 12 ( 3 x − 2 ) 3 d y d x = − 12 ( 3 ( 1 ) − 2 ) 3 , x = 1
y – 2 = –12 (x – 1)
y – 2 = –12x + 12
y = –12x + 14


(b)(i)
Area = ∫ 2 3 y d x = ∫ 2 3 2 ( 3 x − 2 ) 2 d x = ∫ 2 3 2 ( 3 x − 2 ) − 2 d x = [ 2 ( 3 x − 2 ) − 1 − 1 ( 3 ) ] 2 3 = [ − 2 3 ( 3 x − 2 ) ] 2 3 = [ − 2 3 [ 3 ( 3 ) − 2 ] ] − [ − 2 3 [ 3 ( 2 ) − 2 ] ] = − 2 21 + 1 6 = 1 14 unit 2


(b)(ii)
Isipadu janaan
= π ∫ y 2 d x = π ∫ 2 3 4 ( 3 x − 2 ) 4 d x = π ∫ 2 3 4 ( 3 x − 2 ) − 4 d x = π [ 4 ( 3 x − 2 ) − 3 − 3 ( 3 ) ] 2 3 = π [ − 4 9 ( 3 x − 2 ) 3 ] 2 3 = π [ − 4 9 [ 3 ( 3 ) − 2 ] 3 ] − [ − 4 9 [ 3 ( 2 ) − 2 ] 3 ] = π ( − 4 3087 + 4 576 ) = 31 5488 π unit 3


Leave a Comment