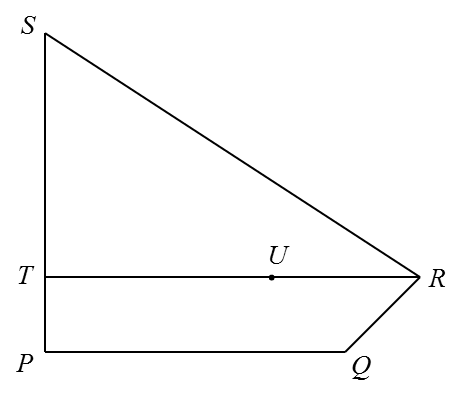
Soalan 3:
Dalam rajah di bawah, PQRS ialah satu segi empat. PTS dan TUR ialah garis lurus.
Diberi bahawa
(a) Ungkapakan dalam sebutan
(i)
(ii)
(b) Tunjukkan titik Q, U dan S adalah segaris.
(c) Jika
(a)
(b)
Oleh itu, Q, U dan S adalah segaris.
(d)

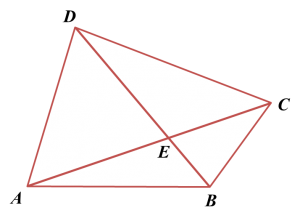
Soalan 4:
Rajah di bawah menunjukkan sisi empat
ABCD. Garis lurus
AC bersilang dengan garis lurus
BD di titik
E.
Penyelesaian:
(a)(i)
(a)(ii)
(b)