8.7.1 Vektor, SPM Praktis (Kertas 2) - Matematik Tambahan SPM

8.7.1 Vektor, SPM Praktis (Kertas 2)

Soalan 1:

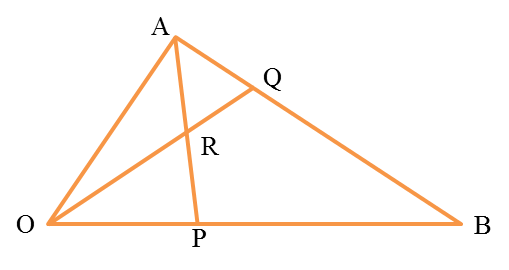
Rajah di atas menunjukkan segi tiga OAB. Garis lurus AP bersilang dengan garis lurus OQ pada titik R. Diberi bahawa

O P = \frac{1}{4} O B, A Q = \frac{1}{4} A B, \vec{O P} = 4 \underset{˜}{b} dan \vec{O A} = 8 \underset{˜}{a} .

(a) Ungkapakan dalam sebutan

\underset{˜}{a} dan \underset{˜}{b} :

(i)

\vec{A P}

(ii)

\vec{O Q}

(b) (i) Diberi bahawa

\vec{A R} = h \vec{A P}, nyatakan \vec{A R} dalam sebutan h, \underset{˜}{a} dan \underset{˜}{b} .

(ii) Diberi bahawa

\vec{R Q} = k \vec{O Q}, nyatakan \vec{A R} dalam sebutan k, \underset{˜}{a} dan \underset{˜}{b} .

\vec{A Q} = \vec{A R} + \vec{R Q},

cari nilai bagi h dan k.

Penyelesaian:

(a)(i)

\begin{array}{l} \vec{A P} = \vec{A O} + \vec{O P} \\ \vec{A P} = - \vec{O A} + \vec{O P} \\ \vec{A P} = - 8 \underset{˜}{a} + 4 \underset{˜}{b} \end{array}

(a)(ii)

\begin{array}{l} \vec{O Q} = \vec{O A} + \vec{A Q} \\ \vec{O Q} = 8 \underset{˜}{a} + \frac{1}{4} \vec{A B} \\ \vec{O Q} = 8 \underset{˜}{a} + \frac{1}{4} (\vec{A O} + \vec{O B}) \\ \vec{O Q} = 8 \underset{˜}{a} + \frac{1}{4} (- 8 \underset{˜}{a} + 4 \vec{O P}) \\ \vec{O Q} = 8 \underset{˜}{a} + \frac{1}{4} (- 8 \underset{˜}{a} + 4 (4 \underset{˜}{b})) \\ \vec{O Q} = 8 \underset{˜}{a} - 2 \underset{˜}{a} + 4 \underset{˜}{b} \\ \vec{O Q} = 6 \underset{˜}{a} + 4 \underset{˜}{b} \end{array}

(b)(i)

\begin{array}{l} \vec{A R} = h \vec{A P} \\ \vec{A R} = h (- 8 \underset{˜}{a} + 4 \underset{˜}{b}) \\ \vec{A R} = - 8 h \underset{˜}{a} + 4 h \underset{˜}{b} \end{array}

(b)(ii)

\begin{array}{l} \vec{R Q} = k \vec{O Q} \\ \vec{R Q} = k (6 \underset{˜}{a} + 4 \underset{˜}{b}) \\ \vec{R Q} = 6 k \underset{˜}{a} + 4 k \underset{˜}{b} \end{array}

(c)

\begin{array}{l} \vec{A Q} = \vec{A R} + \vec{R Q} \\ \vec{A Q} = - 8 h \underset{˜}{a} + 4 h \underset{˜}{b} + (6 k \underset{˜}{a} + 4 k \underset{˜}{b}) \\ \vec{A O} + \vec{O Q} = - 8 h \underset{˜}{a} + 4 h \underset{˜}{b} + 6 k \underset{˜}{a} + 4 k \underset{˜}{b} \\ - 8 \underset{˜}{a} + 6 \underset{˜}{a} + 4 \underset{˜}{b} = - 8 h \underset{˜}{a} + 4 h \underset{˜}{b} + 6 k \underset{˜}{a} + 4 k \underset{˜}{b} \\ - 2 \underset{˜}{a} + 4 \underset{˜}{b} = - 8 h \underset{˜}{a} + 4 h \underset{˜}{b} + 6 k \underset{˜}{a} + 4 k \underset{˜}{b} \end{array}

–2 = –8h + 6k

–1 = –4h + 3k → (1)

4 = 4h + 4k

1 = h + k

k = 1 – h → (2)

Gantikan (2) ke dalam (1),

–1 = –4h + 3 (1 – h)

–1 = –4h + 3 – 3h

–4 = –7h

\begin{array}{l} h = \frac{4}{7} \\ Daripada (2), \\ k = 1 - \frac{4}{7} = \frac{3}{7} \end{array}

Soalan 2:

Diberi

\vec{A B} = (\begin{matrix} 10 \\ 14 \end{matrix}), \vec{O B} = (\begin{matrix} 4 \\ 6 \end{matrix}), dan \vec{C D} = (\begin{matrix} m \\ 7 \end{matrix}), carikan

(a) koordinat A,

(b) vektor unit dalam arah

\vec{O A}

Penyelesaian:

(a)

\begin{array}{l} \vec{A B} = (\begin{matrix} 10 \\ 14 \end{matrix}), \vec{O B} = (\begin{matrix} 4 \\ 6 \end{matrix}) \vec{C D} = (\begin{matrix} m \\ 7 \end{matrix}) \\ \vec{A B} = \vec{A O} + \vec{O B} \\ (\begin{matrix} 10 \\ 14 \end{matrix}) = (\begin{matrix} x \\ y \end{matrix}) + (\begin{matrix} 4 \\ 6 \end{matrix}) \\ (\begin{matrix} x \\ y \end{matrix}) = (\begin{matrix} 10 \\ 14 \end{matrix}) - (\begin{matrix} 4 \\ 6 \end{matrix}) \\ \vec{A O} = (\begin{matrix} 6 \\ 8 \end{matrix}) \\ \vec{O A} = (\begin{matrix} - 6 \\ - 8 \end{matrix}) \\ A = (- 6, - 8) \end{array}

(b)

\begin{array}{l} | \vec{O A} | = \sqrt{{(- 6)}^{2} + {(- 8)}^{2}} \\ | \vec{O A} | = \sqrt{100} = 10 \\ Veckor unit dalam arah \vec{O A} \\ = \frac{\vec{O A}}{| \vec{O A} |} \\ = \frac{(\begin{matrix} - 6 \\ - 8 \end{matrix})}{10} = \frac{1}{10} (\begin{matrix} - 6 \\ - 8 \end{matrix}) \\ = (\begin{matrix} - \frac{3}{5} \\ - \frac{4}{5} \end{matrix}) \end{array}

(c)

\begin{array}{l} Diberi \vec{C D} selari dengan \vec{A B} \\ ∴ \vec{C D} = k \vec{A B} \\ (\begin{matrix} m \\ 7 \end{matrix}) = k (\begin{matrix} 10 \\ 14 \end{matrix}) \\ (\begin{matrix} m \\ 7 \end{matrix}) = (\begin{matrix} 10 k \\ 14 k \end{matrix}) \end{array}

7 = 14k

k = ½

m = 10k = 10 (½) = 5