Soalan 9:
(a) Didapati bahawa 75% daripada murid-murid di SMK Permai pergi ke sekolah dengan menaiki bas. Jika 8 orang murid dipilih secara rawak dari sekolah itu, cari kebarangkalian bahawa selebih-lebihnya 2 orang daripada mereka pergi ke sekolah tidak menaiki bas.
[3 markah]
(b) Jisim ikan yang diternak di dalam sebuah kolam adalah bertabur secara normal dengan min 1.5 kg dan sisihan piawai 0.4 kg . Ikan-ikan itu digred mengikut jisim, seperti yang ditunjukkan dalam Jadual 1, dengan keadaan k ialah pemalar.

(i) Seekor ikan ditangkap secara rawak dari kolam itu, cari kebarangkalian bahawa ikan itu adalah gred A.
(ii) Diberi bahawa 72.84% daripada ikan-ikan di dalam kolam itu adalah gred B.
Wakilkan situasi itu dengan melakar graf taburan normal piawai dan ungkapkan rantau berlorek dalam tatatanda kebarangkalian.
Seterusnya, cari nilai k.
[7 markah]
Penyelesaian:
(a)
$$ \begin{aligned} &\text { Katakan } X=\text { Murid tidak menaiki bas }\\ &\begin{aligned} n=8, q=0.75, p & =1-0.75 \\ & =0.25 \end{aligned} \end{aligned} $$
$$ \begin{aligned} P(x \leqslant 2) & =P(X=0)+P(X=1)+P(X=2) \\ & ={ }^8 C_0(0.25)^0(0.75)^8+{ }^8 C_1(0.25)^1(0.75)^7+{ }^8 C_2(0.25)^2(0.75)^6 \\ & =0.1001+0.2670+0.3115 \\ & =0.6786 \end{aligned} $$
(b)(i)
$$ \begin{aligned} &X \sim N\left(1.5,0.4^2\right)\\ &\begin{aligned} P(X>2) & =P\left(Z>\frac{2-1.5}{0.4}\right) \\ & =P(Z>1.25) \\ & =0.1056 \end{aligned} \end{aligned} $$
(b)(ii)
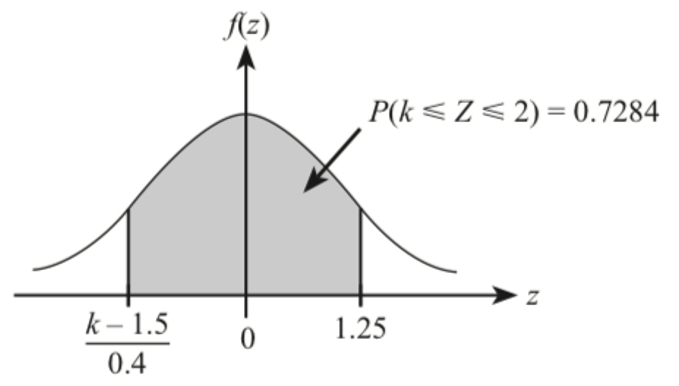
$$ \begin{array}{r} P(k \leqslant X \leqslant 2)=72.84 \% \\ P\left(\frac{k-1.5}{0.4} \leqslant Z \leqslant \frac{2-1.5}{0.4}\right)=0.7284 \\ P\left(\frac{k-1.25}{0.4} \leqslant Z \leqslant 1.25\right)=0.7284 \\ P\left(Z \geqslant \frac{k-1.5}{0.4}\right)-P(Z \geqslant 1.25)=0.7284 \end{array} $$
$$ \begin{aligned} P\left(Z \geqslant \frac{k-1.5}{0.4}\right)-0.1056 & =0.7284 \\ P\left(Z \geqslant \frac{k-1.5}{0.4}\right) & =0.8340 \\ 1-P\left(Z<\frac{k-1.5}{0.4}\right) & =0.8340 \\ P\left(Z<\frac{k-1.5}{0.4}\right) & =0.1660 \\ P\left(Z>\frac{k-1.5}{0.4}\right) & =0.1660 \\ \frac{k-1.5}{0.4} & =-0.97 \\ k-1.5 & =-0.388 \\ k & =1.112 \end{aligned} $$
(a) Didapati bahawa 75% daripada murid-murid di SMK Permai pergi ke sekolah dengan menaiki bas. Jika 8 orang murid dipilih secara rawak dari sekolah itu, cari kebarangkalian bahawa selebih-lebihnya 2 orang daripada mereka pergi ke sekolah tidak menaiki bas.
[3 markah]
(b) Jisim ikan yang diternak di dalam sebuah kolam adalah bertabur secara normal dengan min 1.5 kg dan sisihan piawai 0.4 kg . Ikan-ikan itu digred mengikut jisim, seperti yang ditunjukkan dalam Jadual 1, dengan keadaan k ialah pemalar.

(i) Seekor ikan ditangkap secara rawak dari kolam itu, cari kebarangkalian bahawa ikan itu adalah gred A.
(ii) Diberi bahawa 72.84% daripada ikan-ikan di dalam kolam itu adalah gred B.
Wakilkan situasi itu dengan melakar graf taburan normal piawai dan ungkapkan rantau berlorek dalam tatatanda kebarangkalian.
Seterusnya, cari nilai k.
[7 markah]
Penyelesaian:
(a)
$$ \begin{aligned} &\text { Katakan } X=\text { Murid tidak menaiki bas }\\ &\begin{aligned} n=8, q=0.75, p & =1-0.75 \\ & =0.25 \end{aligned} \end{aligned} $$
$$ \begin{aligned} P(x \leqslant 2) & =P(X=0)+P(X=1)+P(X=2) \\ & ={ }^8 C_0(0.25)^0(0.75)^8+{ }^8 C_1(0.25)^1(0.75)^7+{ }^8 C_2(0.25)^2(0.75)^6 \\ & =0.1001+0.2670+0.3115 \\ & =0.6786 \end{aligned} $$
(b)(i)
$$ \begin{aligned} &X \sim N\left(1.5,0.4^2\right)\\ &\begin{aligned} P(X>2) & =P\left(Z>\frac{2-1.5}{0.4}\right) \\ & =P(Z>1.25) \\ & =0.1056 \end{aligned} \end{aligned} $$
(b)(ii)

$$ \begin{array}{r} P(k \leqslant X \leqslant 2)=72.84 \% \\ P\left(\frac{k-1.5}{0.4} \leqslant Z \leqslant \frac{2-1.5}{0.4}\right)=0.7284 \\ P\left(\frac{k-1.25}{0.4} \leqslant Z \leqslant 1.25\right)=0.7284 \\ P\left(Z \geqslant \frac{k-1.5}{0.4}\right)-P(Z \geqslant 1.25)=0.7284 \end{array} $$
$$ \begin{aligned} P\left(Z \geqslant \frac{k-1.5}{0.4}\right)-0.1056 & =0.7284 \\ P\left(Z \geqslant \frac{k-1.5}{0.4}\right) & =0.8340 \\ 1-P\left(Z<\frac{k-1.5}{0.4}\right) & =0.8340 \\ P\left(Z<\frac{k-1.5}{0.4}\right) & =0.1660 \\ P\left(Z>\frac{k-1.5}{0.4}\right) & =0.1660 \\ \frac{k-1.5}{0.4} & =-0.97 \\ k-1.5 & =-0.388 \\ k & =1.112 \end{aligned} $$