Soalan 12:
Penyelesaian secara lukisan berskala tidak diterima.
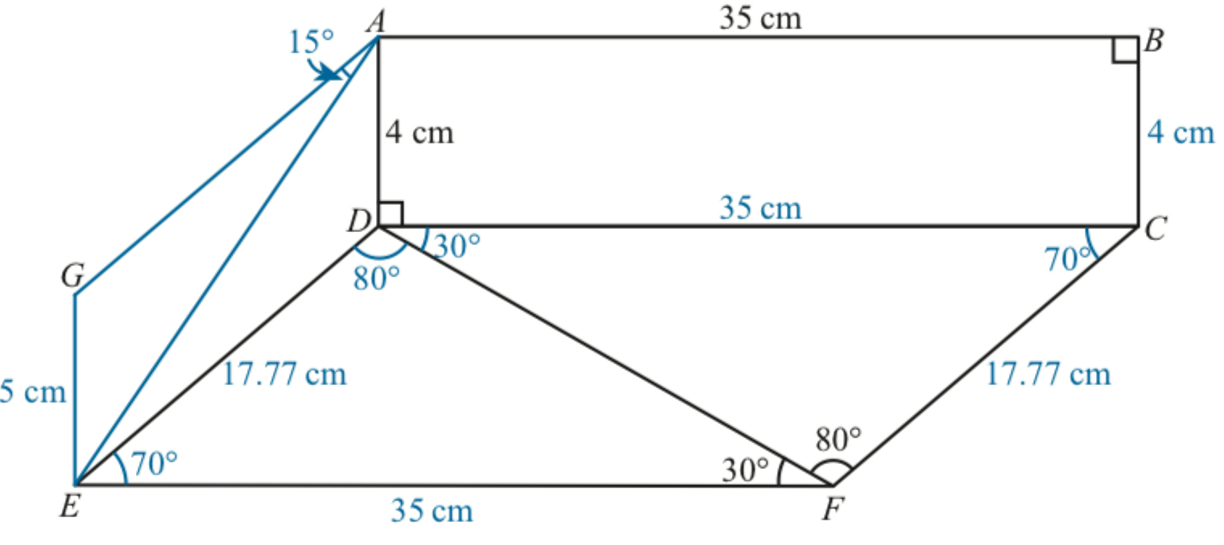
Rajah 6 menunjukkan sebuah model. Model itu terdiri daripada sebuah dinding tegak ABCD dan lantai mengufuk CDEF. CDEF ialah segi empat selari.

(a) Hitung
(i) panjang, dalam cm, bagi CF,
(ii) luas, dalam cm2, bagi Δ ACE.
[6 markah]
(b) Sebatang tiang mempunyai panjang 5 cm. Ia diletakkan secara condong pada bucu E. Sebatang kayu digunakan untuk menyambungkan puncak tiang, G, ke bucu A, dengan keadaan ∠EAG = 15o.
Cari panjang minimum, dalam cm, kayu itu.
[4 markah]
Penyelesaian:
(a)
(i)
$$ \begin{aligned} \frac{C F}{\sin 30^{\circ}} & =\frac{35}{\sin 80^{\circ}} \\ C F & =\frac{35 \sin 30^{\circ}}{\sin 80^{\circ}} \\ C F & =17.77 \mathrm{~cm} \end{aligned} $$
(ii)
$$ \begin{aligned} & A C=\sqrt{35^2+4^2} \\ & A C=35.23 \mathrm{~cm} \end{aligned} $$
$$ \begin{aligned} & C E^2=35^2+17.77^2-2(35)(17.77) kos 110^{\circ} \\ & C E=\sqrt{1966.2118} \\ & C E=44.34 \mathrm{~cm} \end{aligned} $$
$$ \begin{aligned} & A E^2=4^2+17.77^2-2(4)(17.77) kos 90^{\circ} \\ & A E=\sqrt{331.7729} \\ & A E=18.21 \mathrm{~cm} \end{aligned} $$
$$ \begin{aligned} s & =\frac{35.23+44.34+18.21}{2} \\ & =48.89 \end{aligned} $$
$$ \begin{aligned} &\text { Luas } \triangle A C E \\ &\begin{aligned} & =\sqrt{s(s-a)(s-b)(s-c)} \\ & =\sqrt{48.89(48.89-35.23)(48.89-44.34)(48.89-18.21)} \\ & =305.33 \mathrm{~cm}^2 \end{aligned} \end{aligned} $$
(b)
$$ \begin{aligned} \frac{\sin \angle A G E}{18.21} & =\frac{\sin 15^{\circ}}{5} \\ \sin \angle A G E & =0.9426 \\ \angle A G E & =\sin ^{-1}(0.9426) \quad \angle A G E=70.49^{\circ} \end{aligned} $$
$$ \begin{aligned} \angle G E A & =180^{\circ}-15^{\circ}-70.49^{\circ} \\ & =94.51^{\circ} \end{aligned} $$
$$ \begin{aligned} \frac{A G}{\sin 94.51^{\circ}} & =\frac{5}{\sin 15^{\circ}} \\ A G & =\frac{5 \sin 94.51^{\circ}}{\sin 15^{\circ}} \\ A G & =19.26 \mathrm{~cm} \end{aligned} $$
Penyelesaian secara lukisan berskala tidak diterima.
Rajah 6 menunjukkan sebuah model. Model itu terdiri daripada sebuah dinding tegak ABCD dan lantai mengufuk CDEF. CDEF ialah segi empat selari.

(a) Hitung
(i) panjang, dalam cm, bagi CF,
(ii) luas, dalam cm2, bagi Δ ACE.
[6 markah]
(b) Sebatang tiang mempunyai panjang 5 cm. Ia diletakkan secara condong pada bucu E. Sebatang kayu digunakan untuk menyambungkan puncak tiang, G, ke bucu A, dengan keadaan ∠EAG = 15o.
Cari panjang minimum, dalam cm, kayu itu.
[4 markah]
Penyelesaian:
(a)

(i)
$$ \begin{aligned} \frac{C F}{\sin 30^{\circ}} & =\frac{35}{\sin 80^{\circ}} \\ C F & =\frac{35 \sin 30^{\circ}}{\sin 80^{\circ}} \\ C F & =17.77 \mathrm{~cm} \end{aligned} $$
(ii)
$$ \begin{aligned} & A C=\sqrt{35^2+4^2} \\ & A C=35.23 \mathrm{~cm} \end{aligned} $$
$$ \begin{aligned} & C E^2=35^2+17.77^2-2(35)(17.77) kos 110^{\circ} \\ & C E=\sqrt{1966.2118} \\ & C E=44.34 \mathrm{~cm} \end{aligned} $$
$$ \begin{aligned} & A E^2=4^2+17.77^2-2(4)(17.77) kos 90^{\circ} \\ & A E=\sqrt{331.7729} \\ & A E=18.21 \mathrm{~cm} \end{aligned} $$
$$ \begin{aligned} s & =\frac{35.23+44.34+18.21}{2} \\ & =48.89 \end{aligned} $$
$$ \begin{aligned} &\text { Luas } \triangle A C E \\ &\begin{aligned} & =\sqrt{s(s-a)(s-b)(s-c)} \\ & =\sqrt{48.89(48.89-35.23)(48.89-44.34)(48.89-18.21)} \\ & =305.33 \mathrm{~cm}^2 \end{aligned} \end{aligned} $$
(b)
$$ \begin{aligned} \frac{\sin \angle A G E}{18.21} & =\frac{\sin 15^{\circ}}{5} \\ \sin \angle A G E & =0.9426 \\ \angle A G E & =\sin ^{-1}(0.9426) \quad \angle A G E=70.49^{\circ} \end{aligned} $$
$$ \begin{aligned} \angle G E A & =180^{\circ}-15^{\circ}-70.49^{\circ} \\ & =94.51^{\circ} \end{aligned} $$
$$ \begin{aligned} \frac{A G}{\sin 94.51^{\circ}} & =\frac{5}{\sin 15^{\circ}} \\ A G & =\frac{5 \sin 94.51^{\circ}}{\sin 15^{\circ}} \\ A G & =19.26 \mathrm{~cm} \end{aligned} $$