Soalan 10:
Penyelesaian secara lukisan berskala dan vektor tidak diterima.

(a) Diberi bahawa titik-titik B, C dan D adalah segaris dengan keadaan BC : CD = 1 : 3.
(i) Cari koordinat D dalam sebutan h.
(ii) Seterusnya, hitung nilai h jika luas ΔACD ialah 27 unit2.
[4 markah]
(b)(i) P(x, y) bergerak dengan keadaan jaraknya dari titik B dan titik D adalah sama. Menggunakan rumus jarak, cari persamaan lokus P.
(ii) Lokus P memintas paksi-y pada titik E.
Tentukan sama ada garis lurus BA dan garis lurus CE adalah selari atau tidak.
[6 markah]
Penyelesaian:
(a)(i)
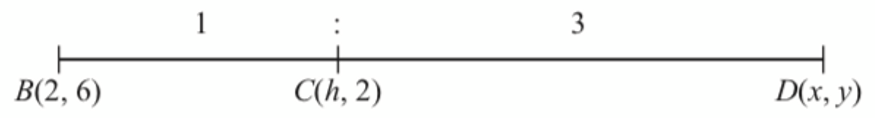
$$ \begin{aligned} C(h, 2) & =\left(\frac{3(2)+(1)(x)}{1+3}, \frac{(3)(6)+(1)(y)}{1+3}\right) \\ & =\left(\frac{6+x}{4}, \frac{18+y}{4}\right) \end{aligned} $$
$$ \begin{aligned} \frac{6+x}{4} & =h \\ 6+x & =4 h \\ x & =4 h-6 \end{aligned} $$
$$ \begin{aligned} \frac{18+y}{4} & =2 \\ 18+y & =8 \\ y & =8-18 \\ y & =-10 \end{aligned} $$
$$ \therefore D(4 h-6,-10) $$
(a)(ii)
$$ \begin{aligned} &\text { Luas } \triangle A C D =27 \text { unit }^2\\ &\frac{1}{2}\left|\begin{array}{cccc} -1 & h & 4 h-6 & -1 \\ 0 & 2 & -10 & 0 \end{array}\right|=27 \end{aligned} $$$$ \left|\begin{array}{c} {[(-1)(2)+(h)(-10)+(0)(4 h-6)} \\ -[(0)(h)+(2)(4 h-6)+(-10)(-1) \end{array}\right|=54 $$$$ \begin{aligned} |(-2-10 h)-(8 h-12+10)| & =54 \\ |-2-10 h-8 h+12-10| & =54 \\ |-18 h| & =54 \end{aligned} $$
$$ \begin{aligned} -18 h & =54 \\ h & =-3(\text { abaikan }) \end{aligned} $$
$$ \begin{aligned} -(-18 h) & =54 \\ h & =3 \end{aligned} $$$$ \therefore h=3 $$
(b)(i)
$$ \begin{aligned} & D(4 h-6,-10) \text { apabila } h=3 \\ & \therefore D(6,-10) \end{aligned} $$
$$ \begin{aligned} B P & =P D \\ \sqrt{(2-x)^2+(6-y)^2} & =\sqrt{(6-x)^2+(-10-y)^2} \\ \sqrt{x^2-4 x+4+y^2-12 y+36} & =\sqrt{x^2-12 x+36+y^2+20 y+100} \\ x^2+y^2-4 x-12 y+40 & =x^2+y^2-12 x+20 y+136 \\ -4 x+12 x-12 y-20 y+40-136 & =0 \\ 8 x-32 y-96 & =0 \end{aligned} $$
(b)(ii)
$$ \text { Pintasan paksi- } y , x=0 $$
$$ \begin{aligned} 8 x-32 y-96 & =0 \\ 8(0)-32 y-96 & =0 \\ -32 y & =96 \\ y & =-3 \end{aligned} $$$$ \therefore E(0,-3) $$
$$ \begin{aligned} & m_{B A}=\frac{6-0}{2-(-1)}=2 \\ & m_{C E}=\frac{-3-2}{0-3}=\frac{5}{3} \\ & m_{B A} \neq m_{C E} \end{aligned} $$
∴ BA adalah tidak selari dengan CE.
Penyelesaian secara lukisan berskala dan vektor tidak diterima.

(a) Diberi bahawa titik-titik B, C dan D adalah segaris dengan keadaan BC : CD = 1 : 3.
(i) Cari koordinat D dalam sebutan h.
(ii) Seterusnya, hitung nilai h jika luas ΔACD ialah 27 unit2.
[4 markah]
(b)(i) P(x, y) bergerak dengan keadaan jaraknya dari titik B dan titik D adalah sama. Menggunakan rumus jarak, cari persamaan lokus P.
(ii) Lokus P memintas paksi-y pada titik E.
Tentukan sama ada garis lurus BA dan garis lurus CE adalah selari atau tidak.
[6 markah]
Penyelesaian:
(a)(i)
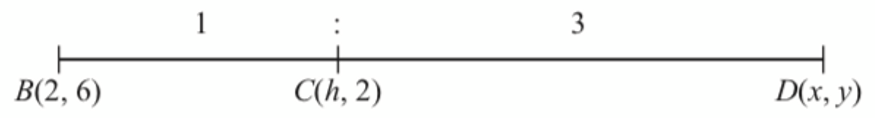
$$ \begin{aligned} C(h, 2) & =\left(\frac{3(2)+(1)(x)}{1+3}, \frac{(3)(6)+(1)(y)}{1+3}\right) \\ & =\left(\frac{6+x}{4}, \frac{18+y}{4}\right) \end{aligned} $$
$$ \begin{aligned} \frac{6+x}{4} & =h \\ 6+x & =4 h \\ x & =4 h-6 \end{aligned} $$
$$ \begin{aligned} \frac{18+y}{4} & =2 \\ 18+y & =8 \\ y & =8-18 \\ y & =-10 \end{aligned} $$
$$ \therefore D(4 h-6,-10) $$
(a)(ii)
$$ \begin{aligned} &\text { Luas } \triangle A C D =27 \text { unit }^2\\ &\frac{1}{2}\left|\begin{array}{cccc} -1 & h & 4 h-6 & -1 \\ 0 & 2 & -10 & 0 \end{array}\right|=27 \end{aligned} $$$$ \left|\begin{array}{c} {[(-1)(2)+(h)(-10)+(0)(4 h-6)} \\ -[(0)(h)+(2)(4 h-6)+(-10)(-1) \end{array}\right|=54 $$$$ \begin{aligned} |(-2-10 h)-(8 h-12+10)| & =54 \\ |-2-10 h-8 h+12-10| & =54 \\ |-18 h| & =54 \end{aligned} $$
$$ \begin{aligned} -18 h & =54 \\ h & =-3(\text { abaikan }) \end{aligned} $$
$$ \begin{aligned} -(-18 h) & =54 \\ h & =3 \end{aligned} $$$$ \therefore h=3 $$
(b)(i)
$$ \begin{aligned} & D(4 h-6,-10) \text { apabila } h=3 \\ & \therefore D(6,-10) \end{aligned} $$
$$ \begin{aligned} B P & =P D \\ \sqrt{(2-x)^2+(6-y)^2} & =\sqrt{(6-x)^2+(-10-y)^2} \\ \sqrt{x^2-4 x+4+y^2-12 y+36} & =\sqrt{x^2-12 x+36+y^2+20 y+100} \\ x^2+y^2-4 x-12 y+40 & =x^2+y^2-12 x+20 y+136 \\ -4 x+12 x-12 y-20 y+40-136 & =0 \\ 8 x-32 y-96 & =0 \end{aligned} $$
(b)(ii)
$$ \text { Pintasan paksi- } y , x=0 $$
$$ \begin{aligned} 8 x-32 y-96 & =0 \\ 8(0)-32 y-96 & =0 \\ -32 y & =96 \\ y & =-3 \end{aligned} $$$$ \therefore E(0,-3) $$
$$ \begin{aligned} & m_{B A}=\frac{6-0}{2-(-1)}=2 \\ & m_{C E}=\frac{-3-2}{0-3}=\frac{5}{3} \\ & m_{B A} \neq m_{C E} \end{aligned} $$
∴ BA adalah tidak selari dengan CE.