Soalan 3:
(a) Buktikan
\(\frac{2\tan x}{2-\mathrm{sek}^2x}=\tan2x.\)
(b) (i) Lakar graf y = – tan 2x untuk 0 ≤ x ≤ π.
(b) (ii) Seterusnya, dengan menggunakan paksi yang sama, lakar satu garis lurus yang sesuai untuk
mencari bilangan penyelesaian bagi persamaan
\(\frac{3x}\pi+\frac{2\tan x}{2-\mathrm{sek}^2x}=0\)
untuk 0 ≤ x ≤ π.
Nyatakan bilangan penyelesaian itu.
Penyelesaian:
(a)
\(\begin{array}{l}\frac{2\tan x}{2-\mathrm{sek}^2x}=\tan2x\\\\\text{Sebelah kiri:}\\\frac{2\tan x}{2-\mathrm{sek}^2x}=\frac{2\tan x}{2-{(1+\tan^2x)}}\\=\frac{2\tan x}{2-\tan^2x}\\=\tan2x\text{(Sebelah kanan)}\end{array}\)
(b)(i)
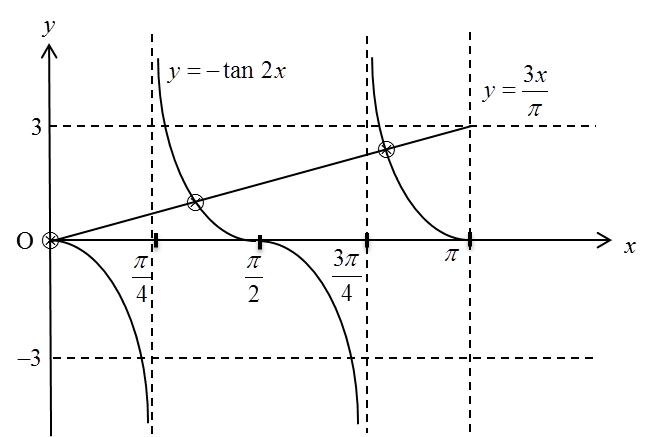
(b)(ii)
\(\begin{array}{l}\frac{3x}\pi+\frac{2\tan x}{2-\mathrm{sek}^2x}=0\\\frac{3x}\pi+\tan2x=0\leftarrow\boxed{\text{dari (a)}}\\-\tan2x=\frac{3x}\pi\\\text{ }y=\frac{3x}\pi\\\\\text{Graf yang sesuai dilakar ialah }y=\frac{3x}\pi.\end{array}\)
Apabila x = 0, y = 0
Apabila x = π, y = 3
Bilangan penyelesaian = 3